Абсолютная и условная сходимость знакочередующегося ряда

Для знакочередующегося ряда особое значение имеет не просто исследование его сходимости, а установление характера данной сходимости. Рассматривают абсолютную и условную сходимости знакочередующегося ряда.

Знакочередующийся ряд 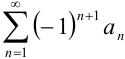называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов .

Заметим по определению, что исследование абсолютной сходимости знакочередующегося ряда фактически сводится к исследованию сходимости положительного ряда. Таким образом, для этой цели можно использовать все признаки сходимости положительных рядов.

Пример №34.3.

Докажите, что знакочередующийся ряд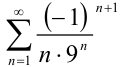
абсолютно сходится.

Доказательство. Составим ряд из модулей членов данного ряда: .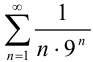

Исследуем полученный положительный ряд на сходимость с помощью признака Даламбера по алгоритму.

1. Найдём :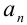

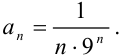
2. Найдём :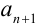

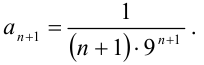
3. Найдём :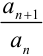

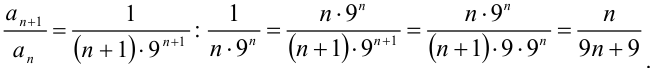
4. Найдём :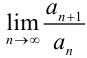

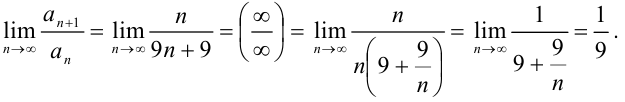
В итоге, 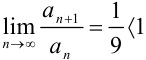. Значит, по признаку Даламбера ряд 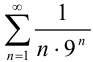сходится. Следовательно, по определению знакочередующийся ряд 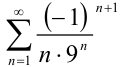абсолютно сходится,
что и требовалось доказать.

Для абсолютно сходящихся рядов справедливо утверждение, которые мы сформулируем без доказательства.

Утверждение. Если знакочередующийся ряд абсолютно сходится, то он и просто сходится.

В силу данного утверждения, знакочередующийся ряд 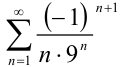, рассмотренный в примере 34.3., сходится.

Знакочередующийся ряд 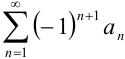называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов , расходится.

Пример №34.4.

Докажите, что знакочередующийся ряд 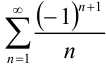условно сходится.

Доказательство. Исследуем сходимость знакочередующегося ряда с помощью признака Лейбница по алгоритму.

1. Выпишем модуль общего члена исходного ряда: .
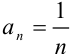2. Найдём 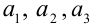: 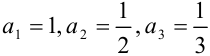. Неравенства 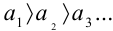справедливы, т.к. 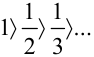(первое условие признака Лейбница выполнено).
3. Найдём 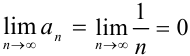(второе условие признака Лейбница выполнено).

Следовательно, по признаку Лейбница знакочередующийся ряд 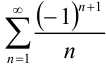сходится.

Исследуем сходимость ряда, составленного из модулей членов данного знакочередующегося ряда. Ряд 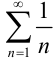является расходящимся гармоническим рядом. Следовательно, по определению знакочередующийся ряд 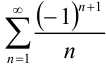условно сходится, что и требовалось доказать.

Для определения характера сходимости знакочередующегося ряда 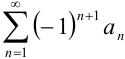удобно использовать следующий алгоритм:

1. составить ряд из модулей членов данного ряда: ;
2. исследовать положительный ряд на сходимость;
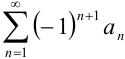3. если ряд сходится, то знакочередующийся ряд абсолютно сходится (следовательно, и просто сходится);
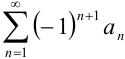4. если ряд расходится, то исследовать знакочередующийся ряд на сходимость;
5. сделать вывод об условной сходимости знакочередующегося ряда .

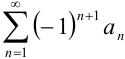Пример №34.5.

Исследуйте характер сходимости знакочередующегося ряда .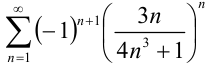

Решение:

Для исследования характера сходимости знакочередующегося ряда 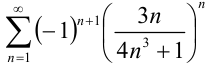воспользуемся алгоритмом.

1. Составим ряд из модулей членов данного ряда: .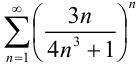

2. Исследуем полученный положительный ряд 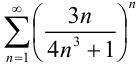на сходимость с помощью признака Коши, т.к. общий член ряда представляет собой 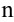-ую степень выражения :

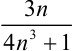• выпишем :
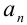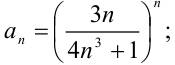
• найдём :
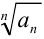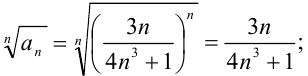
• найдём :

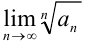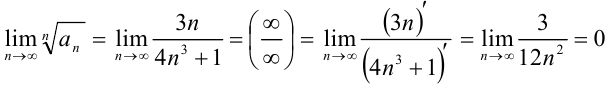
(при раскрытии неопределенности 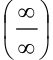использовали правило Лопиталя). В итоге, 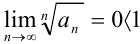. Значит, по признаку Коши ряд 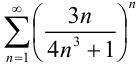сходится.

3. Поскольку ряд 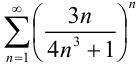сходится, то по определению, знакочередующийся ряд 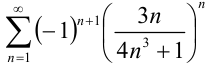абсолютно сходится (следовательно, и просто сходится).

Ответ: 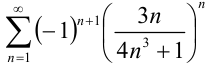абсолютно сходится.

Пример №34.6.

Исследуйте знакочередующийся ряд 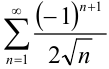на абсолютную и условную сходимость.

Решение:

Для исследования характера сходимости знакочередующегося ряда 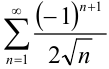воспользуемся алгоритмом.

1. Составим ряд из модулей членов данного ряда: .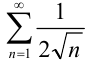

2. Исследуем полученный положительный ряд 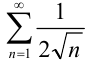на сходимость. Поскольку он получается из расходящегося гармонического ряда 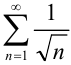умножением на 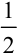то, согласно свойству числовых рядов (свойство 2 лекции 32), он расходится.

3. Из расходимости ряда 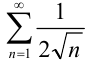следует, что абсолютно сходящимся знакочередующийся ряд 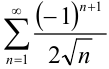не будет.

4. Исследуем знакочередующийся ряд 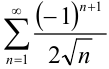на сходимость с помощью признака Лейбница по алгоритму:

• выпишем модуль общего члена исходного ряда:
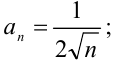
• найдём 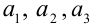: 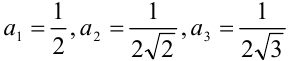. Неравенства 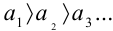справедливы, т.к. 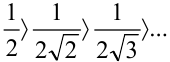(первое условие признака Лейбница выполнено);
• найдём 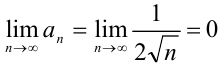(второе условие признака Лейбница выполнено).

Следовательно, по признаку Лейбница знакочередующийся ряд 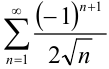сходится.

5. Поскольку знакочередующийся ряд 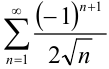сходится, а ряд из модулей его членов расходится, то по определению, 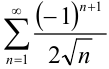условно сходится.

Ответ: 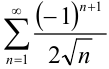условно сходится.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Интегральный признак Коши.

Понятие знакочередующегося ряда. Признак Лейбница.

Свойства абсолютно сходящихся рядов.

Понятие функционального ряда.