Оглавление:



Частотная характеристика двухполюсника
2-частотная характеристика терминального устройства. Входное сопротивление 2-терминального устройства и его входная проводимость являются функцией частоты.
- Частотная зависимость действительной и мнимой частей входного сопротивления или входной проводимости 2-терминального устройства называется частотной характеристикой 2-терминального устройства.
Частотные характеристики широко используются в радиотехнике и связи. Людмила Фирмаль
Они рассчитываются, если схема внутреннего соединения 2-терминальной сети и значения активного сопротивления, индуктивности и емкости в ней известны или экспериментально удалены.
Когда частотная характеристика снимается экспериментально, на вход схемы подается напряжение, частота которого может сильно варьироваться, и по результатам измерений вычисляются действительная и мнимая части входного сопротивления. 2-терминальная схема может включать индукторы, конденсаторы и активные резисторы, соединенные последовательно и параллельно.
- Наиболее интересными являются частотные характеристики 2-терминального устройства, состоящего только из индуктивности и конденсаторов. 2 когда частота терминального электропитания высока, индуктивное сопротивление индуктора гораздо выше чем внутреннеприсущее сопротивление катушки, упростить конструкцию частотных характеристик, последнее часто ignored.
In такая идеальная упрощенная схема, только индуктивность и емкость существуют. В качестве примера рассмотрим частотные характеристики 2-оконечных устройств, показанных на рисунке 1. 119, А и d. In рис. 1199, а образован последовательно соединенными индуктивностью LJ и емкостью CI.
и конфигурация частотных характеристик схемы значительно упрощена. Людмила Фирмаль
Биполярная диаграмма 119, параллельное соединение g-L и C2.При построении частотных характеристик предположим, что отсутствуют потери энергии в реактивном сопротивлении всех элементов, входящих в состав 2-терминального устройства. 2 входное сопротивление терминального устройства и входная проводимость рис. 119, и равны
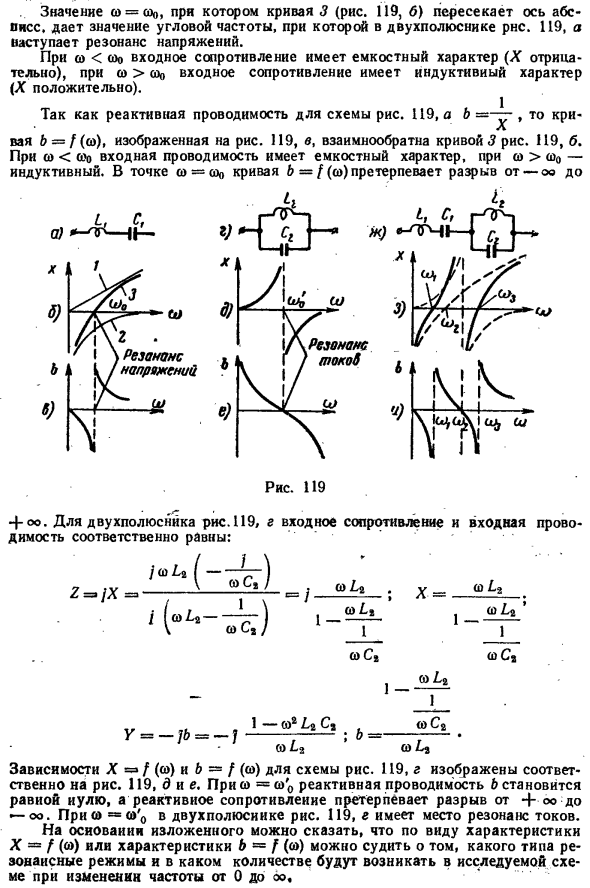
Прямая 1 на рис. 119, б показана зависимость wZq-f (ω).Кривая 2-зависимая — = /(o).Кривая 3-зависимость X = / (ω). Используйте C\■**. 。 • 。Уровень CO = Кок. Кривая 3 (рис. 119, 6) пересекает горизонтальную ось. 2 показано значение угловой частоты в терминальной сети. 119, и возникает резонанс напряжения. в ω<ОО, входное сопротивление имеет емкостный (х-отрицательное), а при ω> ку, входное сопротивление носит индуктивный характер (х-положительное).
Реактивное сопротивление цепи на рисунке равно 119, а б, тогда кривая b = f (co), 119c показана на рисунке, кривая 3 рисунка и обратная 119, Б. для ω<ω0 входная проводимость является емкостной, но для ω> coo она индуктивна. в точке co = coo кривая 6 = f (co) находится из-oo- Рисунок 119 4-ОО.
В случае 2-терминальной сети, рис. 119, G входное сопротивление и входная проводимость равны coLg Один Зависимость схемы на рисунке X = > /(ω) и b = /(ω) 119, g соответственно показана на рисунке. 119, di e. при ω= co’o реактивное сопротивление равно нулю, а реактивное сопротивление разрывается от 4°C до°C. 2 в терминальной сети, когда ω=ω ’ o, рис. 119, возникает резонанс тока f.
Исходя из вышеизложенного, по типу характеристики X = f (co) или характеристике b = f(co) можно определить, какой тип резонансной Моды и какая величина возникнет в рассматриваемой схеме при изменении частоты от 0 до oo.
Точка, в которой кривая (X = f© пересекает ось абсциссы(или, соответственно, кривая b = f (w) становится прерывистой от-oo до 4 oo), дает рассматриваемой схеме значение угловой частоты, при которой возникает резонансный режим напряжения. Точка, в которой кривая X = f (ω) становится прерывистой от oo до-oo (или кривая b = f © пересекает абсциссу), соответствует текущей резонансной моде.
В качестве примера сформулированного правила исследования построим частотные характеристики X = f © и b = f © схемы на Рис.1. 119, g и из них определяют возможные резонансные Моды и величины в цепи, когда частота изменяется от 0 до ОО. Для 2-терминальной сети, рис. 119, реактивное сопротивление w равно суммарному реактивному сопротивлению 11-терминальной цепи на Рис. 2, 119, a и D.
В зависимости от этого его можно получить суммированием продольных координат кривой X = f ©, ординаты 119, g и кривой X (co) схемы на рис. X. 119, b и d (см. рис. 119, h). Зависимость b » f (sv) для схемы фиг. 119, g показано на рисунке. 119, И. Из рисунка 119, А и видно на диаграмме фиг.
Когда частота увеличивается от 119, g, 0 до oo, это выглядит так: (b = bx, возникает резонанс напряжения, еслиb = b2, возникает резонанс тока, (b = bc3, снова появляется режим резонанса напряжения. Отметим, что схема не имеет резонансной частоты, переменного тока и напряжения резонансных режимов.
Смотрите также:

