Оглавление:


Толстостенные цилиндры
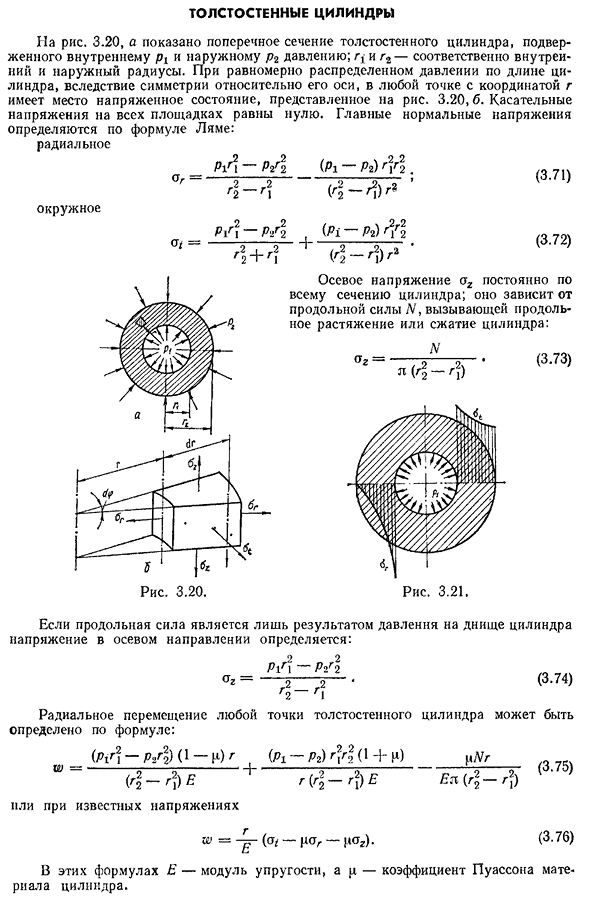
- Толстостенный цилиндр Для риса. 3.20, и указывает поперечное сечение толстостенного цилиндра, который подвергается внутреннему и внешнему давлению P2, g/и G2-соответственно
внутреннему и внешнему радиусу. При давлении, равномерно распределенном по длине цилиндра, за счет симметрии относительно его оси, в любой точке с координатами g возникает напряженное состояние, которое показано на рисунке.
3.20 b. касательное напряжение на всех участках равно нулю. Основное Людмила Фирмаль
вертикальное напряжение определяется формулой Лэмба: радиальное Р-Л-Р-РЛ СТГ=Г2-Г2 g2G1 (3.71) Окружность РК? — РК? (.Пи ра) линии irq2 р (’г-Г1) (3.72) Святой= / 3.20 рис Осевое напряжение СТГ является постоянным по поперечному сечению цилиндра и зависит
от продольной силы N, вызывающей продольное натяжение или сжатие цилиндра: Н л(G22-Г2) (3.73) Рис 3.21 4+ ’ 21 2_2 ’2G1. Точки Толстого цилиндра следующие (Пи-РГ)+ч ) Если продольная сила является только результатом давления в нижней части цилиндра,
- то осевое напряжение определяется следующим образом: — Lil. (По г = —————— — 7а чемпионы\ Любое радиальное смещение определяется формулой: (R1G1-P2′, 2) (1-I ____________________ (G22-г? )Е+г(Г2-Г2)е л(Г2 -, 2) в’»»’ Пли при известном напряжении Ш=-^(ст/—рстг). (3.76) в этих
формулах E-модуль упругости, а p-коэффициент Пуассона материала цилиндра. Только для внутреннего давления 50B уравнения (3.72)и(3.75) упрощаются (3.71), (3.77) (3.78) зта
Распределение радиальных и окружных напряжений в поперечном сечении цилиндра в этом случае показано на рисунке. 3.21 Самое сильное Людмила Фирмаль
место находится внутри При g=HaKC0t = P1 максимум°g В g = r2 = P1 min^g=0. (3.80)) Расчетные уравнения под действием внутреннего давления только по третьей теории прочности М [о] — 2Р L на теории энергии изменения формы [п][а]-/3^ (3-81) (3.82))
Смотрите также:
| Теории прочности | Напряжения в составных толстостенных цилиндрах |
| Тонкостенные сосуды | Контактные напряжения |

