Оглавление:

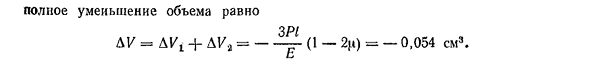

Относительное изменение объема
- Относительные изменения объема При упругой деформации объем большинства материалов увеличивается при растяжении
и уменьшается при сжатии. Только в частных случаях Р,=0,5 (парафин) объем деформации ПРН не изменяется.
В общем случае напряженного состояния относительное изменение объема Людмила Фирмаль
равно:©=&x + Wu + ez=+s2+E3= УЛ Ф. (3.35 )) Где o — +гг+_gj+К2+К3. Три. −3 Коэффициент объемной деформации (объемный модуль) y. E A-3(1-2ts) Или =4-t a^°-(ф3-36>нормальная составляющая напряжения в относительном изменении объема: 0^. =Х0-Ф-2Gsx
Дж=Х6-Ф-2Ge^;другие формы: о-=2Г(ех-Е); О—а=2Г(сы); АГ-а = 2Г(ГУ-г); (3.38)где X=7р -:-г-п———п -— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — -) Г2^0 2Gez. (3.37) Рис 3.14. Один. И экс+ЕС+£г е ———— ———— Компонент тангенциального напряжения: B^^x y’tyz^^YG>^GX(3.39)
- в частном случае линейного напряженного состояния объем материала стержня, подвергнутого растяжению, может быть записан как: K1=Y[1+b(1-2)). Абсолютное изменение объема AV=V f-V = Vs (1-
2|x). Относительное изменение объема вычисляется по формуле: e==- = e(1-2J1). (3.40)) Для изменения площади поперечного сечения: абсолютный AF=-2 / x-p-F; относительный AF-p — =-2 / x. Например. Уменьшите объем стального стержня (E=2 * 105 МПа), рассчитайте сжимающую осевую силу. Стержень имеет два сечения с
различной площадью поперечного сечения(рис. 3.14), I=2 см, P=450 кН и/х=0,3. Людмила Фирмаль
Решение. Уменьшение объема первой секции Аки=_4F/(1_2I) — —— (1 — 2|x); во втором разделе Р21 Ава=- — — — — (1-2к); 43 полная потеря веса DU=Al/t + LU2=ZR1 — Ми- (1-2C)=-0. 054cm3.
Смотрите также:
| Компоненты малой деформации | Потенциальная энергия упругой деформации |
| Зависимости между напряжениями и деформациями в пределах упругости. закон Гука | Теории прочности |

