Оглавление:




Учет собственного веса при растяжении и сжатии
- Собственный вес описание натяжения и сжатия Влияние собственного веса учитывается тогда, когда его величина соизмерима со значением приложенной нагрузки. При определении продольных сил и напряжений при расчете деформации N-значение потенциальной энергии с- 27 собственный вес последнего
рассматривается как распределенная нагрузка, действующая вдоль оси элемента. Интенсивность этой нагрузки равна: qx=yFK, (2.15) y-насыпной вес материала (кг / см3); Fx-площадь поперечного сечения X балки. Продольная сила сечения x собственного веса определяется нормальным напряжением NX=§qx dx, o a в этом сечении О= Х
Форекс Расширение пучка от собственного веса в области X = 0 до x=a: Людмила Фирмаль
О потенциальной энергии деформации, собранной на этом участке: A M R®Nzd? x o помимо собственного веса, если балка подвергается сосредоточенной нагрузке, напряжения и деформации определяются на основе принципа независимости силы, действующей отдельно от концентрации и мертвого веса. Фиксированный участок штанги(рис. 2.12). Сила любого сечения x Nx равна UEX, максимальная сила N=yFl, требуемая площадь поперечного сечения XJ» (2.16) (2.17)
(2.18) (2.19) Длина- Пять. Я «» ’1′ — Ч Рис 2.12 ф= — А. Раздел Х Ox=ух, напряжение УГ; наибольшее напряжение ох=уг; длина предел З1 Макс=г Удлинитель Потенциальная энергия деформации стержня в^?3 6Е При наличии нагрузки Максимальное напряжение (2.20 утра)) (2.21) (2.22) (2.23) (2.24) P сила Nx-P+yfx, напряжение в этом разделе P , °ч=~р+(2.25) П °Макс=—+У1′ 28 ненужные поперечные сечения Ф= —- —— о-Ил (2.26) И полное расширение луча (2.27) Приведенная выше
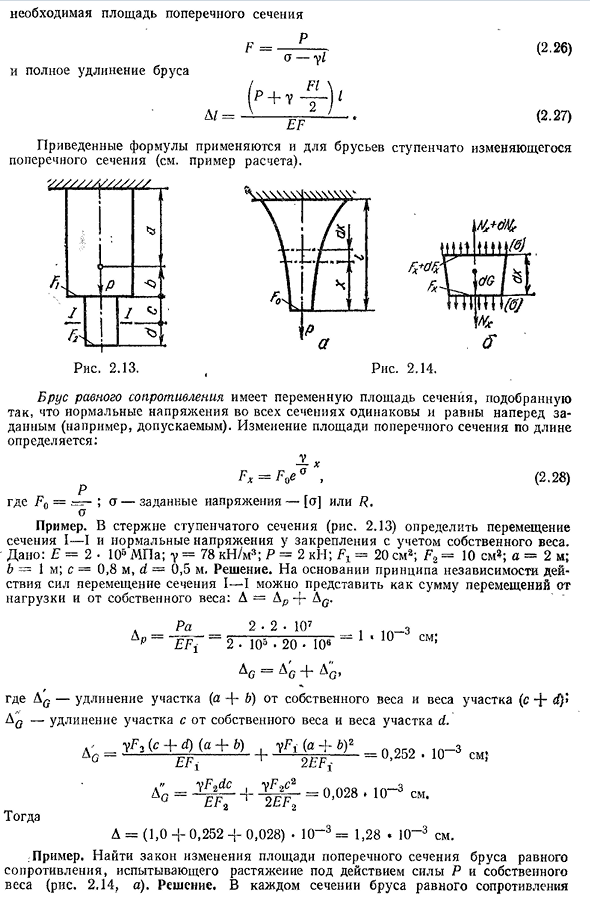
- формула также применима к строке раздела (см. примеры расчета). Ступенчатое изменение zzzzzzzzz/yzzzzzzzz с gshmw & Стержень равного сопротивления имеет переменную площадь поперечного сечения, выбранную таким образом, чтобы нормальные напряжения во всех сечениях были равны одинаковым и предписанным (например, допустимым). Изменение площади поперечного сечения по длине、: Fx=враг A X, (2.28) П Где Fo=; o-заданное напряжение-[o] или R. O пример. Стержень ступенчатой части (рис. 2.13), принимая
во внимание собственный вес, определяют перемещение поперечного сечения I-I и обычное напряжение в момент крепления. Дано: Е=2 * 105мпа; г=78kN/м3;Р=2кн; модель FJ=20 см2;Л2=1см*;о=2м; в = 1м; в=0,8 м, д=0,5 M раствора. Исходя из принципа независимости силового перемещения секции I-I, его можно выразить как сумму перемещений от груза и собственного веса: L=Dr4-AE. п — РА Эфи 2 • 2 • 107 105 * 20 * 10E=1•10-3cm; Два. ^Г. Где AE-длина участка мертвого груза (a+B)и масса участка (C+rf)>AFL-собственный вес участка d и протяженного участка с весами. Например. Испытывая напряжение под действием силы Р и собственного веса,
находим закон изменения площади поперечного сечения балки равного Людмила Фирмаль
сопротивления (рис. 2.14, а). Решение. В каждом сечении пучка одинаковое сопротивление 29 напряжение равно заданному[a] или R. 2.14 b): DNX на-ДГ=0. Давайте перейдем к напряжению: Когда вы интегрируетесь, вы получаете f dFx [St]dFx-yFx dx=0 или. Ноль один ДХ; гонка FX=-■Х+О Или Здесь, ко=ЕС. Константа интегрирования определяется из граничных условий! х = о Форекс = Фо=; — Д- = C0e[ој = со. l u[St] [St] и закон изменения площади разреза приобретает следующий вид: ох Так, в стержне равного сопротивления поперечное сечение изменяется по логарифмическому закону. Например. Для P=300TC, I=40m, [St]=10kgf/cm2, для кладки y=2,5 кгс/cm3, E=2X105kcm / cm2, а также веса моста из щебня в виде брусков одинакового сопротивления сжатию, определяют верхний и Нижний. Площадь верхнего сечения Площадь нижней секции Десять. Масса устоев кладки Q=Ft[St] P=10>8 и 16. 101-300 000=516TC; объем кладки У2. 5*10-3
Смотрите также:
| Эластика Эйлера | Расчет гибких нитей |
| Расчет по разрушающим нагрузкам | Способ сравнения деформаций |

