Оглавление:



Дифференциальные зависимости между силовыми величинами
- Дифференциальная связь между силовыми параметрами. Уравнение (30.4) определяет соотношение между внешним моментом и внутренним тангенциальным моментом. Как было показано в§ 173, при ограниченном кручении тонкостенных стержней возникают
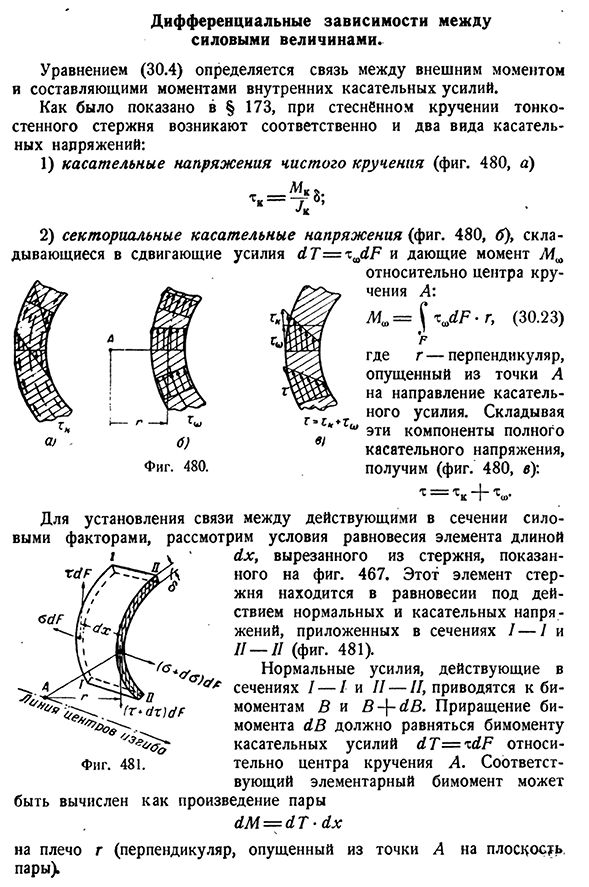
соответственно два вида касательных напряжений: 1) касательное напряжение чистого кручения (рис. 480, а) Переходим к смене Установить связь между 2) касательное напряжение сектора (рис. 480, b), сдвиговая сила d T=x jlF, дающая момент к центру кручения
a:^J F-r, (30.23) где g перпендикулярно направлению касательной силы Людмила Фирмаль
из точки A. Эти дополнительные компоненты получают полное напряжение сдвига. 480, а): По коэффициенту силы, действующей на поперечное сечение, рассмотрим условие равновесия элементов dx-отрезка по длине от стержня, как показано на рисунке. Этот элемент стержня 467 находится в равновесии под действием нормальных и касательных напряжений, приложенных к участкам
1 — /и II-II(рис. 481). Вертикальные силы, действующие на сечения I-I и II-II, сводятся к b и B — \ — d B. приращение Бимомента dB должно быть равно бимоменту тангенциальной силы d T=td F к центру кручения A. Фигура. 481. Г плеча (вертикальное, опущенное из точки А в плоскость, парное).§ 176] дифференциальная связь между B, Ml и W547 Имея в виду, что силы dt возникают на каждом базовом
- участке в разделе、: Или (30.24) Фигура. 482. дБ-Д х ТШ * Р Д Ф]. Это легко доказать, используя интегральную формулу в части 1). Кроме того, для второго интеграла J hshg dP9, согласно уравнению (30.23)представляет изгибающий момент., Фактически, R=u, A^D F-dv, и интегрируя J f C d v=|u o j^ — §v d u, мы получаем следующее: v=JrK dF=0, чистый поворот t^d F для раздела F. Поскольку O=0, I[IO-O du]=0g, т. е. J TCG dF=0. Ф БД-Г X•или~ Получено производное соотношение, аналогичное известному дифференциальному соотношению между
изгибающим моментом и поперечной изгибающей силой. D х * Рассмотрим случай постоянно изменяющегося внешнего момента нагружения стержня по длине стержня. Это, например, случай, когда стержень изгибается равномерно распределенной нагрузкой d, расположенной на плоскости, не совпадающей с линией центра изгиба. В этом случае внешний крутящий момент, создаваемый непрерывной нагрузкой M9-MX, изменяется по длине стержня.
Мерой изменения величины момента MX является сила непрерывной Людмила Фирмаль
крутящей нагрузки, указанная т. — G=548 основа расчета тонкостенных стержней[гл. XXX Выберите из длины стержня элемент d x и создайте условие его равновесия(рис. 482), мы получим — (АФ#V Т D х — [г-L4x-о Или (30.25)) Дифференциальная зависимость, аналогичная DQ, получена для соответствующего уравнения-Q, которое выражает зависимость между поперечной силой и прочностью непрерывной нагрузки.
Смотрите также:

