Оглавление:






Вычисление напряжений и деформаций.
- Расчет напряжений и деформаций. А. метод определения напряжений и деформаций, используемый для решения некоторых специфических задач комплексного сопротивления, ограничивается рассмотрением стержня призмы, где центр изгиба совпадает с центром тяжести поперечного сечения в более сложных случаях силового воздействия на тело, например на стержень(рис. 451) находится в равновесии под действием приложенной к нему системы сил, так как находится в пространстве. Как использовать только 451 для упрощения чертежа показана способность к концентрации;
однако внешние силы могут также рассеивать пары нагрузки и силы-дальнейшие рассуждения от этого не изменятся. Чтобы найти напряжения в сечении, разделенном на МНФ и две части, перпендикулярные оси балки (I и II), сначала отметим, что эти напряжения вызваны общим случаем комплексного сопротивления 518[гл. XXIX Рассмотрите возможность отбрасывания части бара, например правой и балансировки левой. Мы используем
декартову систему координат; начало координат расположено на центроиде Людмила Фирмаль
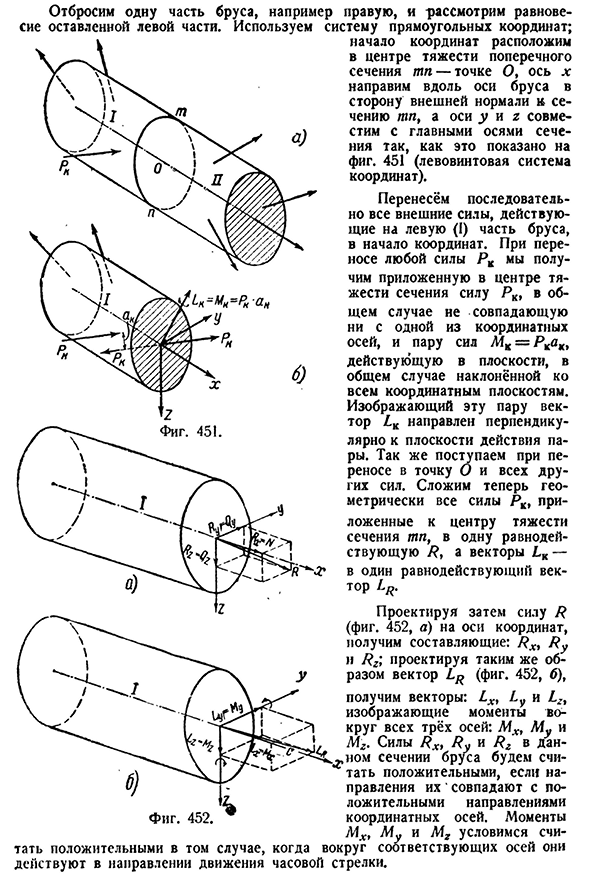
поперечного сечения TP-точка O, ось x-451 (левая система координат) на оси стержня по направлению к внешней нормали к сечению TP. Все внешние силы, действующие на левую (I) Часть луча, непрерывно передаются в начало координат. При передаче любой силы P K мы получаем силу p K, приложенную к центру тяжести сечения, которая в общем случае не совпадает ни с одной из осей координат, а пара сил L4K=P KK одинакова.、 Вектор K, представляющий эту пару, направлен перпендикулярно рабочей плоскости пары. Точку
О и проделайте то же самое при переносе на все остальные силы. Теперь добавим всю силу P K, приложенную к центру тяжести сечения TP, к одному результату R геометрически и добавим вектор 1K к одному результирующему вектору-Тору LK. Затем проецируется сила R(рис. 452, а) на координатных осях вы получаете компоненты R x, r y, 7?d; спроецировать вектор таким же образом(Рис. 452, б), получаем вектор: Lx, L? И ЦТС обратил на мгновение все вокруг трех осей: МХ, Му и М2. Силы R x, r y и R2 в этом сечении балки считаются положительными, если их направлениесовпадает с положительным направлением координатных осей. Моменты MX, Mu и M2 условимся
- считать положительными величинами при действии в направлении движения по часовой стрелке вокруг каждой оси.§ 169] расчет напряжений и деформаций 619 Таким образом, в результате передачи сил мы можем заменить систему внешних сил P K, действующих на левую сторону балки. С незапамятных времен было известно, как каждый из этих шести компонентов влияет на левую часть штанги. В рассматриваемом разделе положительная составляющая/?^(=2U) — вертикальная сила-вызывает сжатие на левой стороне балки; изгибающий момент Μ и боковая сила 0? (=7?г) — плоскость xz\изгиба каждого момента M изгиба и сдвига балки? И боковая сила Qy (= / ?
изгиба и сдвига в плоскости XY\момент компании AFX вызывает скручивание пучка вокруг оси абсцисс. Таким образом, в наиболее распространенных случаях действия силы штанги существует четыре простых варианта: осевое растяжение-или сжатие, два плоских изгиба и кручение. B. составим формулу для расчета нормального напряжения и тангенциального напряжения в любой точке A с координатами y и z, расположенной в первом квадранте разреза TP( 453). В этом случае предположим, что все шесть составляющих системы внешних сил положительны(рис. 452). В сечении ТП существуют нормальные и тангенциальные напряжения, которые уравновешивают эту систему. Нормальные напряжения
изгибающего момента и изгибающего момента уравновешиваются равномерно распределенными сжимающими напряжениями. 453). Людмила Фирмаль
Положительные изгибающие моменты Mu и Mg уравновешиваются нормальными напряжениями a» и a «соответственно, а следовательно, и положительными моментами Mu l и «2». В точке А имеется сжимающее напряжение а«== — — — — — и положительный момент от м2-растягивающее напряжение AG’P==. Суммирование этих составляющих нормального напряжения дает формулу для вычисления полного нормального напряжения в точке D: Под действием про-мг. От положительного про -. То < г=а, 4 −9 «4 —® ’» = — — (29.1)’ * у ЮЖД Для вычисления суммарного нормального напряжения в других точках поперечного сечения балки достаточно подставить значения a\Mu и A в Формулу (29.1)и координаты y и g в знак. Предполагая, что в Формуле (29.1) напряжение a равно нулю,
указывая координаты точек нулевой линии, проходящей через y y и z0, чтобы найти расположение этой линии, получим следующую формулу: Комплексное сопротивление общего случая N520[гл. XXIX Отрезки Y и z, отрезанные нулевой линией по осям, равны (рис. Четыреста пятьдесят четыре.): (29.2) (29.3) J2N Jy N a y T m; и Касательная угла наклона нейтральной линии (θ) к оси Y равна: Л М у’ Нейтральная линия обычно делит поперечное сечение балки на две области: растяжение и сжатие (рис. 454). Проведя линию, параллельную нейтрали и касательную к другой области, контуру поперечного сечения, находим в ней и удаленные от нейтральной
линии точки 1 и 2 подставляя координаты этих точек (yi и Zi или z2) в уравнение (29.1), получаем максимальное значение растягивающего и сжимающего напряжений ((2)—p^7 (1,2)±J^.2) — < 2 9-4) тангенциальное напряжение поперечного сечения TP возникает вследствие закручивания балки вокруг оси x и смещения ее плоскостей XY и xz. Крутящий момент MX уравновешивается тангенциальным давлением TC. Для стержней с поперечным сечением в виде круга или кольца эти напряжения рассчитываются по формуле (§ 57: Т с-г•(29.5) (29.6) Для стержня с поперечным сечением другой формы используйте формулу, приведенную
в§ 67(таблица 17): M X Шах Т К * Во всех случаях наибольшее касательное напряжение возникает на контуре поперечного сечения и направлено по касательной к контуру. Напряжение сдвига, уравновешивание силы Qy и Q2i обычно играют второстепенную роль; они следуют уравнению>(§ 91): Тонны _Q y S (y) и t<нет. (?(А)ЮЖД Б(г) г~~Jyb(з)- (29.7) Для прямоугольных и круглых сечений тангенциальное напряжение (29.7) является максимальным на соответствующей главной оси инерции: х Определение этих напряжений часто нецелесообразно, поскольку общее
тангенциальное напряжение от двух плоских изгибов достигает наибольшего значения на центроиде сечения, то есть нулевого тангенциального напряжения от кручения и нормального напряжения от изгиба. В связи с тем, что нормальное напряжение изгиба и тангенциальное напряжение кручения достигают наибольшего значения на контуре поперечного сечения, обычно необходимо найти наибольшее напряжение-§ 169]напряжение и напряжение. Проверьте прочность материала балки. Точка с максимальным касательным напряжением не всегда согласуется с точкой, в которой возникает максимальное нормальное
напряжение. Таким образом, в наиболее тяжелых условиях материал балки находится в точке контура, где достигается наиболее неблагоприятное сочетание нормальных и касательных напряжений. Такими точками могут быть точки с наибольшим нормальным напряжением, точки с наибольшим касательным напряжением и любые промежуточные точки профиля профиля. При необходимости можно также учитывать тангенциальное напряжение, возникающее при изгибе. Для того чтобы проверить прочность материала в наиболее общем случае действия силы на балку, сравнивая расчетное значение напряжения, рассчитанн
ое по формуле§ 94[уравнение (15.14-15.17)] или§ 167[уравнение (28.1)] уравнения (15.14-15.17) или (28.1), мы нашли один из двух существенных вопросов: значение напряжения. B. To вычисляя смещение призмы пучка ’ оснащенной системой сил, так как она находится во Вселенной, мы применяем принцип независимости силового воздействия(это можно сделать с помощью методики, ранее изложенной в соответствующем разделе курса§ 161). Вспомним использование теоремы Кастильяно (§ 126), не прибегая к другим методам. Потенциальная энергия деформации при комплексном
сопротивлении балки, учитываемая здесь, может быть выражена как сумма величин энергии от всех составляющих N, Qy, Qz, Mype, Mz. Игнорируя энергию тангенциального напряжения при изгибе, получим U=U(N)+U(Mx)+U (My)+U(Mz). (29.8) написал следующее уравнение для энергии элементов балки длиной dx, предполагая, что нормальная сила N и крутящий момент MX обычно не остаются постоянными по длине балки. Но И(М Х)=^ — , И для энергии в длине Z часть древесины: Для энергии нормального напряжения в плоскости изгиба, соответственно, имеем следующее уравнение (§ 125): В этом отношении выражение (29.8) принимает вид: U (29.9)
Смотрите также:
| Способ сравнения деформаций | Учет собственного веса и сил инерции |
| Расчёты балок конечной длины | Статически неопределимые конструкции |

