Оглавление:



Вычисление опорных реакций и построение эпюр для неразрезных балок
- Поддержка реакции и расчет плана для непрерывного луча. Возьмем N-й пролет (рис. 378); основная система представляет собой шарнирную опорную балку, на которую воздействуют несколько внешних нагрузок, а опорный момент и МП уже известны. Воспользуемся методом сложения силового воздействия; тогда i-й
пролет опорной реакции, левый R^i и правый R», содержит три члена: первый, внешний и внутренний. Фигура. 378 рис. Триста семьдесят девять Индекс буквы R(рис. 378 и 379) среднее: чем выше число пролетов, тем ниже число опор.
Каждая пара сил, приложенных к шарнирной опорной балке, равна моменту пары, деленному Людмила Фирмаль
на пролет, и вызывает реакцию в противоположном направлении. Учитывая опорные моменты и положительные моменты MP, мы получаем: =+(23.25) 1P1P ^=5’+^ -^. (23.26) Чтобы найти идеальную реакцию каждой промежуточной опоры непрерывной балки, необходимо суммировать реакцию соседних пролетов. Так, если вызвать полную реакцию, то получится за количество букв R-опор
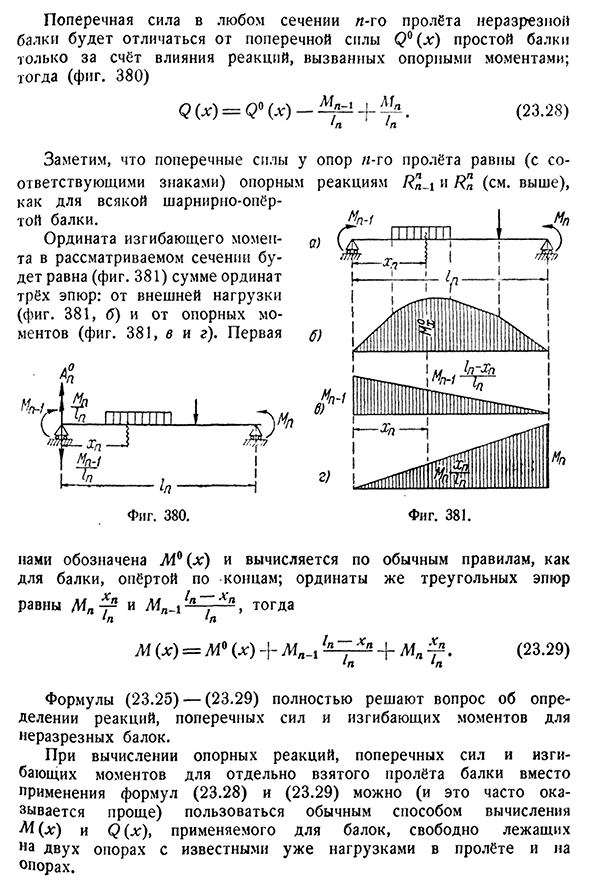
а с одним индексом внизу-d-я опора(рис. Триста семьдесят девять): p__p l|p p p+1-i \ n CP•(23.27)§ 145] график непрерывного луча 457 Поперечная сила в поперечном сечении / Z-м пролете непрерывной балки отличается от поперечной силы Q°(x) простой балки только из-за эффекта реакции, обусловленного опорным моментом. Триста восемьдесят) 1P1P (23.28)) Обратите внимание, что боковая сила
- опоры пролетного строения ZZ-ro равна (с соответствующим знаком) реакции опоры и (см. выше), а также любой шарнирной опорной балке. Вертикальная ось изгибающего момента рассматриваемого сечения будет равна(рис. 381)сумма трех участков по вертикальной оси: от внешней нагрузки(рис. 381, Б) и от опорного момента(фиг. 381, B и D). Первый Фигура. 380 рис. Триста восемьдесят один Обозначим L4°(x), вычисленное по обычному правилу, для балки, поддерживаемой на концах, вертикальная ось треугольника равна
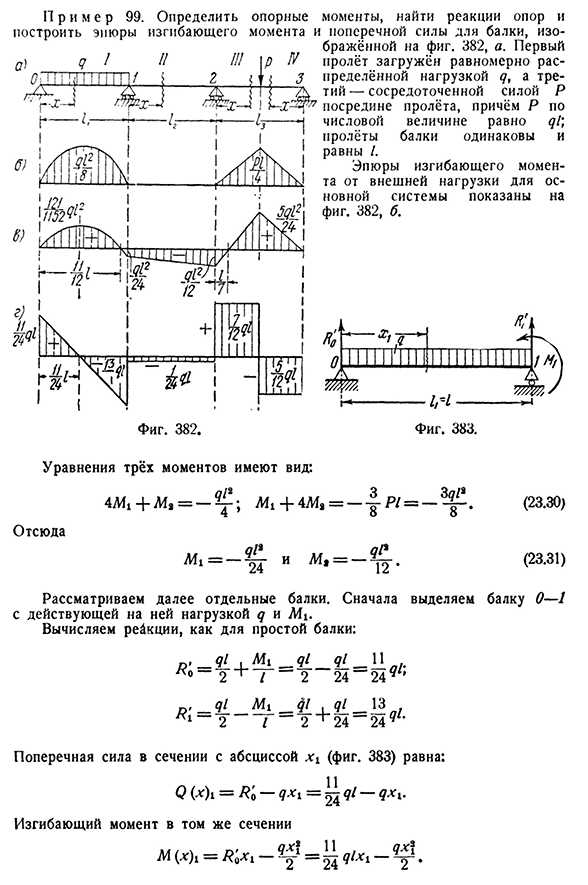
MD-T5, тогда М(х)=В0(х)+Ш»_1+МП. (23.29) * p1P Уравнение (23.25) — (23.29) полностью решает задачу определения реакции, поперечной силы и изгибающего момента непрерывной балки. Вместо использования уравнений (23.28) и(23.29), обычный метод вычисления (x) и Q (x) при расчете реакции опоры, поперечной силы и изгибающего момента одного пролета балки называется 458 статически неопределенным ВАЛКОМ[CH. XXIII ПП Уол и PP9999 мм.. Опорный момент Ooppreeddeelliitt, найти опору реакции и построить график изгибающего момента и боковой силы для балки, показанной на рисунке. 382, а. первый g-пролет равномерно RAS-5-нагружен сосредоточенной нагрузкой q, а третий-сосредоточенной силой P в середине пролета, причем P равно численному QL.
На рисунке показан изгибающий момент от внешней нагрузки основной Людмила Фирмаль
системы. 382, б. Фигура. 382. Уравнение трех моментов О! КЛ У1 Один. GC я ГМ Один. И так оно и есть. Имеют форму: 4Mt+a l,= — M1+4L ZDR8 * (23.30) qP K, Яр Двадцать четыре И LG » −12•(23.31) Далее рассмотрим отдельные балки. Во-первых, выберите балки 0-1 с нагрузкой, действующей на q и Mi. Рассчитайте реакцию, как простой луч:.. А * призраки 2 «г» 2 24-24″ Поперечное сечение боковой силы 1-2/-2″G24-24″ (рис. 383) равно: Q () i=r’o-qxi=ql-qxi. Изгибающий момент в том же интервале m (x) i=R^Xi — ^l=^q lX t -^.§ 145] участок 459 для непрерывного валка Выберите второй пролет в виде еще одной балки 1-2(рис. 384); он нагружен только опорными выступами Mi и M2. Мы повторяем весь процесс расчета: L4! Mg^/_ _ И1. 1 ~ 1 ^ 1 24 12 —
24′ / ?- О! — _4L,. — Мне 24 ’12-24′ Последняя треть пролета 2-3, две секции(рис. Триста восемьдесят пять), / ? Г 2~2/~2″G12-12″» П M2_q л__12″T2h М (х) 3=ш=л Q я-м (х) 8=/?’»Х Z+м я=_l, за м[х призраки. М(х) Т= — Р3’= — ~КЖ -, м(х) 4= » Х4=qixt. Валовая эталонная реакция определяется путем суммирования эталонной реакции на каждом носителе, рассчитанной отдельно выше: РО-П-2^Джей?4=/?;+/?Т=^/ — г=г;/?,=Р+/? ; «=Г4-_L9/=г Q л. Р»=р’3″=в КЖ. * Сумма всех реакций равна заданной нагрузке: P ql-2ql. На рисунке показана диаграмма изгибающего момента и поперечной силы, составленная из расчетных данных. 382, in, G. максимум отображается с x=^/и равен y^ ^ 8.
Смотрите также:
| Расчёт неразрезных балок. | Неразрезные балки с консолями. Балки с защемлёнными концами |
| Теорема о трёх моментах | Примеры расчёта неразрезных балок |

