Оглавление:





Определение деформаций балок переменного сечения
- Определение деформации балки переменного сечения. При определении прогиба и поворота балок с переменным поперечным сечением следует отметить, что жесткость таких балок является функцией X. E J(x) d2y д Х2 Здесь J (x) — переменный момент инерции поперечного сечения балки. Прежде чем интегрировать это уравнение, можно выразить J (x) через соответствующую замену J на J (x), то есть момент инерции части, на которую действует 7itah. Покажем это на примере выше. Определите отклонение луча равного сопротивления(рис. 311), зажатый с одного конца, нагружается
с другого конца силой Р и имеет определенную высоту. На свободном конце балки выберите начало координат. Затем Ш(х)= — р х; Д х)= — с^ = ^ ^ — = 7 ^ — , (20.6) Дифференциальное уравнение £ 7 4 — ^=~P x-i dx2 принимает следующий вид:£7-g — = — ^ — = — P Z. (20.7) EJ= — P1x+C; E. Jy= — P l^+C x — [- D. Для определения интегральной константы имеем условие: в точке x=1, прогибы j/=0 и угол поворота — ^ — =0,
или 0=P P — \ — C и 0=+c Z4-D ; И так оно и есть. C=R R и D=R R. Выражения Людмила Фирмаль
Y и 0 принимают вид d_dy _ _ Pl. ПППП x1dx-Эдж Р х’EJ-Эдж L1I гпотребителям * ППК PP_PPP г. 0х. х s1Y~~2EJ+EJ2EJ~2EJ|/2И+р г Максимальное отклонение на свободном конце луча будет равно x=0. Jmax-PR• * 396 балка переменного сечения [гл. ОБМАН Если вся балка постоянного сечения выполнена в момент инерции J, то максимальное отклонение составит/p / 3 / max — —. Один. Это меньше, чем в il — £ — Pa3a. Поэтому балка переменного сечения
обладает большей гибкостью по сравнению с балкой постоянной жесткости той же прочности. Именно поэтому они используются не только для экономии материала, но и для таких конструкций, как пружины. Уравнение (20.7) показывает, что кривизна луча в данном примере постоянна. Между тем, в результате интегрирования мы получаем параболические уравнения и предоставляем студентам объяснить, почему это произошло. Применение графоаналитического метода для определения деформации балки в деформированном
- поперечном сечении также не представляет трудностей. Вместо того чтобы делить изгибающий момент и боковую силу фиктивной балки на жесткость EJ для расчета f и 6, график момента главной балки как фиктивной нагрузки, а затем делить на жесткость EJ для расчета f и 6. е=м Сильф. Если обобщить этот метод на балку переменного сечения, то L4 (x) Нагрузите фиктивную балку этой нагрузкой, как изгибающим моментом, так и поперечной силой в поперечном сечении фиктивной балки, чтобы получить желаемый угол отклонения и поворота. В приведенном выше примере q’J= = — gPjx-l= — Dr! j, т. е. f, иктивная кбалка, сплошная не треугольная, а равномерно распределенная нагрузка(рис. 317). Отклонение
поперечного сечения B, равное изгибающему моменту в зажиме фиктивной балки, выражается формулой Р/Да2.- Мы можем сказать, что наша балка имеет определенную жесткость EJ, и ее график изгибающего момента может быть вычислен путем умножения определения деформации балки на коэффициент§ 123]переменного сечения 3 9 7 в каждом продольном гнезде. p Re°bra s o V A n a I график момента будет иметь вертикальные координаты н P X E1 ″ съел p7EJ(x)-P x EJx-P l(рис. 318); затем граф по общему правилу аналитического метода», = — » • 4 = — ? — > = — £ • ЭДЖ Таким образом, определение отклонения балки переменного сечения может
привести к такому же поведению для балки постоянной жесткости, но с моментом. П р и М Е Р88. 319, А) в середине пролета I с Людмила Фирмаль
сосредоточенной нагрузкой Р определить аналитическое отклонение графически под нагрузкой Р для балки, свободно лежащей на двух опорах. Момент инерции сечения левой половины балки равен J, а правая преобразует график момента Фиктивная балка отображается путем преобразования нагрузки. 319 дюймов Реакция манекена слева равная. Я ПЛ И2. 1Pl I1P1\L1~2’4′ 2 ’W+ 2′ 2 ′ 2 ’3 — 1 2′ мнимый изгибающий момент и отклонение точки C в сечении C следующие: _l I, 1/Pl I_PP, PPP9M/S-f2′ 2 2 * 4 6 24 ′ 96 32 * ПП 32′ П р и М Е Р89. Определите отклонение луча, зажмите один конец и приложите концентрацию к другому концу (рис. 320, а). Половина балки имеет поперечное сечение больших размеров, J2 7 балок переменного сечения£398[CH. ОБМАН Преобразуем график
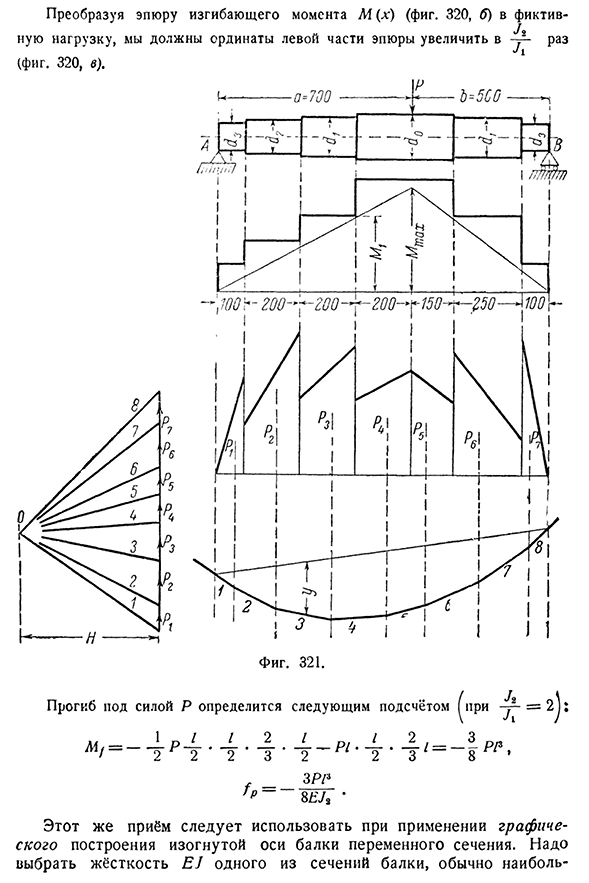
изгибающего момента M (x) (рис. 320, б) при фиктивной нагрузке необходимо увеличить вертикальную ось левой стороны участка Определяется прогиб под действием силы Р 1 1 1 2 2^22 3 Следующий счет идет в _ — — — — p i^. _литр. JL i — __1R / W2 2 3 8′ SP / 3 ’£8WA’ При применении графической конфигурации криволинейной оси балки переменного сечения необходимо использовать ту же технологию. Необходимо выбрать один жесткий EJ сечения балки, а обычно самый-123] определение варианта балки переменного сечения 399 Затем для главного из них преобразуем график момента и строим канатный многоугольник с расстоянием полюса, равным EJ (§ 120.
Вертикальная ось многоугольника, построенная в обычном порядке, представляет собой отклонение луча. Метод преобразования участков особенно полезен, когда поперечное сечение балки изменяется ступенчато, а не непрерывно. Примените этот метод к конструкции криволинейной оси вала, описанной в предыдущем пункте. Структура показана на рисунке. Участок из 321 момента имеет форму треугольника, равного наибольшей ординате ^т ч — Я люблю рай. 5000 • 70 • 50 Сто двадцать. =145 500кгсл. Диаметр D вала и соответствующий ему момент инерции следующие Шестьдесят четыре. Значение: Диаметр сечения момент инерции см см Ноль. 16 3217 Один. 14, 1886. Два. 12, 1018. Три. Десять.
Четыреста девяносто один Вертикальная ось графика момента равна L16=D x1, что соответствует переходу с участка диаметром 16e l на участок диаметром 14e= = 2 1 0 0 * 5 0 = 1 0 5 000 после преобразования он будет равен 105 000 * =180 000 кгсм. Все остальные граничные координаты преобразуются таким же образом. Кроме того, канатные полигоны, изображающие изогнутую ось вала, уже построены известным способом.
Смотрите также:
| Подбор сечений балок равного сопротивления | Постановка вопроса |
| Практические примеры балок равного сопротивления. | Вычисление потенциальной энергии |

