Оглавление:



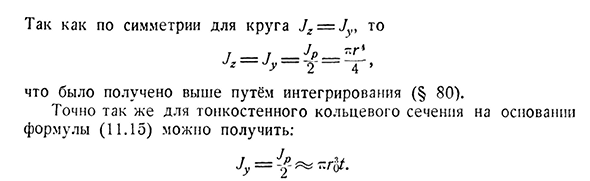

Зависимость между моментами инерции при повороте осей
- Соотношение между моментами инерции оси вращения#центральной оси вы можете потратить столько, сколько захотите. Для этого рассмотрим, как изменяется момент инерции на двух осях, перпендикулярных друг другу при повороте на угол а, не может ли момент инерции для произвольной центральной оси
быть выражен как функция момента инерции для одной или двух различных осей. Возьмите фигуру и протяните через ее центроид O две взаимно перпендикулярные оси OU и Oz(рис. 197). Каковы осевые моменты инерции для этих осей JY, Jz и JY Z центробежной инерции? Вычертим вторую систему осей x и z x, первую наклоненную
под углом a; положительное направление этого угла сохраняем началом координат при повороте оси вокруг точки O. через известные Людмила Фирмаль
моменты инерции J и JZ выражаем моменты второй системы координат осей Jy и J’z. Запишем уравнение для момента инерции для этих осей.: Дя=(З и ДФ\ Ф Ф ДЖ дж;=дж з; ДФ’, Дж’,=J и г; ДФ. Р Р Р Р Р (14.9) 278 расчет момента инерции плоской фигуры[гл. XIV Из чертежа мы видим, что координаты площадки DF в системе ИО-вернулись ось Y^Оз^являются J/J в=ое—ЕС=ое—БД=потому что А4-з Син а=ад-ДК=ад-
быть=потому что-Й грех. Подставляя эти значения y t и z t в Формулу (14.9), можно увидеть, что Jy=J(G cos a-y sin a) 2dF= = §(z2cos2a-Р. U2sin2a-2Д/г грешить, потому что а) ДФ, Ф (14.10)) Точно так же: (I. Одиннадцать) J’2=J (y cos A z sin a) 2dF (14.12) (14.13) Или J’Z=sin2A J z2dF-J-cos2A J y2dF4-sin2a J y Z dF. Первые два интеграла уравнения(14.11)и(14.12) представляют осевые моменты инерции Jv
- и Jzt, а последний-центробежный момент инерции области относительно этих осей Jyg. Далее, Jy=JY cos2a-sin2a-Jy z sin2a, 1Jg=Jy sin2a4-Jx cos2a4-JyZ sin2a. J для решения этой задачи при повороте с одной оси на другую относительно центробежного момента инерции(рис. 197)мы: Джей уя — ^ы из Х ф д, Где z и Z x вычисляются по формуле (14.10).Дя с=Дж(з ЗША Г, потому что а) (з потому что-Й грех)ДФ — = грех z2dF$ — грех, потому что Дж/2dF4~cossay_y^ДФ-sin2a й з ДФ. После преобразования J’y z=^ — (Jy-Jg)sin2a4-Jy f cos2a. (14.14)§ 83] центральный момент инерции 279 Поэтому для того, чтобы
рассчитать момент инерции для любой центральной оси y, необходимо рассчитать инерционный момент на системе для любых двух взаимно перпендикулярных центральных осей OU и Og. Чтобы вычислить одинаковые значения Jy, Jz, JyZ, выделите ось y и ось z, разделите площадь рисунка на такие составные части, и переход от центральной оси каждого компонента к ним на параллельную ось фактически сделает это, как показано ниже в Примере. В этом расчете сложная фигура должна быть разделена на такую фундаментальную часть, где значение Центрального момента инерции для системы осей, перпендикулярных друг другу, известно как можно больше.
Таким образом, формулы(14.13) и (14.14) являются формулами для Людмила Фирмаль
перехода из одной системы в другую с осью, ортогональной друг другу, независимо от центра или нет. Из Формулы (14.13) можно еще раз сделать вывод между моментами инерции при вращении оси. Добавить формулы для Дя и J в непосредственной близости от отеля(14.13);получить/г+л=/г (cos2a-Ф-sin2a)—ЮЖД (sin2a-Ф-cos2a)=дя-\ — ЮЖД, (14.15), т. е. сумма моментов инерции для любой вертикальной оси Y и Z, если подставить формулу (14.15) вместо как JY и JZ (14.9), получаем: J в ЛП ДФ=ДП,(14.16) Здесь p=]l y*-(- G2—расстояние) значение dF от точки O Jp=P2dF есть, как уже известно, полярный момент инерции сечения относительно точки O (§ 58).
Момент инерции полярности сечения относительно точки равен сумме осевых моментов инерции относительно оси, перпендикулярной друг другу, проходящей через эту точку. Поэтому эта сумма остается постоянной при вращении оси. Зависимость (14.16)может быть использована для упрощения расчета момента инерции. Поэтому для круга мы уже имели (§ 58) расчет момента инерции 280-плоскостной фигуры[гл. XIV Из симметрии окружности Jz=Jy, то Это было получено выше путем интеграции (§ 80). Аналогично можно получить для тонкостенного кольцевого сечения на основе формулы (11.15: Дя= — П-
Смотрите также:

