Оглавление:





Вычисление моментов инерции и моментов сопротивления для простейших сечений
- Расчет момента инерции и сопротивления простых сечений. В § 78 момент инерции сечения для этой формы Называется нейтральным осевым интегралом: J=J z-dF. (13.7) где z-расстояние от нейтральной оси базовой площадки dF. Возьмем в качестве примера расчет этого интеграла для прямоугольника(рис. 187) высота h и ширина B. Мы рисуем вокруг оси симметричные Oz и Oh, через ее центр тяжести. Когда действует внешняя сила§ 80] момент
инерции простейшего участка 271 На балке, расположенной в плоскости Ozf нейтральной оси будет ось OU, найдем момент инерции этой оси сначала относительный, затем момент сопротивления площади прямоугольника. Всю площадь поперечного сечения следует разделить на участок dF, узкий прямоугольный шириной b и высотой dz(рис. 187). Затем ДФ=державц б И Интеграл J принимает вид: Чтобы выполнить интеграцию по всей площади прямоугольника, необходимо изменить z с-y на-y (МИЛЛИЛИТР)
Два. В тот момент, когда мы получаем, В связи с тем же сопротивлением / Людмила Фирмаль
х Разделить J на GT и x=y. ОУ нейтральной оси ЧД Если нужно рассчитать момент инерции и сопротивление прямоугольника относительно оси Oz, то нужно поменять местами полученные формулы b и h: , _гемоглобин Стандартом JSS ~ 12 И =(14.3) Заметим, что если сдвинуть все полоски dF=b d z, то сумма произведений z * dF не изменится(рис. 187) параллельно самим себе, так как они расположены в параллелограмме ABCD(рис. 188).Расчет момента инерции 272-го плоского рисунка[гл. XIV Таким образом, момент инерции параллелограмма ABCD относительно оси y равен моменту
инерции квадрата, равного ей: При расчете момента инерции окружности радиуса g (рис. 189) кроме того, ширина этих полос b-b (z) также будет переменной\деление площади на узкие полосы размера dz вдоль оси oz Фигура. Сто восемьдесят девять На высоте секции. Небольшая детская площадка ДФ=б (з) ДЗ. Момент инерции равен: Так как верхняя и нижняя половины сечения одинаковы, то расчет момента инерции оказывается достаточным для нижней половины, и результат удваивается. Предел изменения Z равен 0 и g: Введем новый интегральный переменный угол (рис. Затем з=Г, потому что г; ДЗ=-г г г да грех, Сто восемь девятнадцать); Б(г) — 2Р грех г. Таким
- образом, г=0а= ’ ГС; З=Р=0, 0TS Джей—2Y2r4cos2y sin2y. г-да= с — J sin2 да г-(14.4) тс Ноль. И Вт=Дж= ’ = ~г.\ Т А ч г (14.5) Для круга все оси, проходящие через центр тяжести, являются осями симметрии. Поэтому формулы(14.4) и (14.5) подходят для таких осей.§ 80] момент инерции простейшего участка 273 Для треугольников(рис. 190) момент инерции для оси AB равен jab=^B zdzza -, bz=b^ — LL-b^ — ^ , Ф В следующей главе показано, как рассчитать момент инерции участка сложной формы для произвольной оси. На практике чаще всего встречаются симметричные сечения: для дерева-прямоугольники и круги, для металла-двутавровые балки и Т-
образные сечения(рис. 191). Возможно использование таблицы OST (ассортимента) для прокатки профиля, размеров и Одиннадцать. Фигура. Сто девяносто один R7777777L Фигура. Сто девяносто два Это фабрика, которая производит значение J W профиля. Эти таблицы включены в приложение IX, и их использование указано в нижеследующих пунктах. Для балок из металла обычно используют сложные поперечные сечения, так как их материал можно использовать более экономично, чем поперечные сечения,
например, прямоугольные или круглые. Мы видели (§ 58), что вал выполнен полым, чтобы удалить часть слабо работающего материала. При Людмила Фирмаль
изгибе материала балки вблизи нейтральной оси она принимает небольшое нормальное напряжение[формула (13.9)] и не может быть использована полностью. Таким образом, материал снимается с нейтральной оси, часть его сохраняется, часть перемещается в верхнюю и нижнюю зоны балки, чтобы она работала более интенсивно, с прямоугольным поперечным сечением, получилось (рис. 192) из профильной двутавровой балки с прямоугольным поперечным сечением, имеющей такую же прочность и меньший вес. Применение двутавровых балок целесообразно для материалов,
одинаково устойчивых к растяжению и сжатию(большинство металлов). Сечение в виде марки может быть выполнено, если оно вызвано особой конструкционной ситуацией, или любым из материалов, таких как чугун, бетон, которые обладают сопротивлением растяжению. В последнем случае необходимо, чтобы напряжения крайних волокон были различными. Как видно из вышеизложенного, при определении наиболее экономичной конструкции сечения, стремятся получить максимальный момент сопротивления и момент инерции в одной и той же области F, что
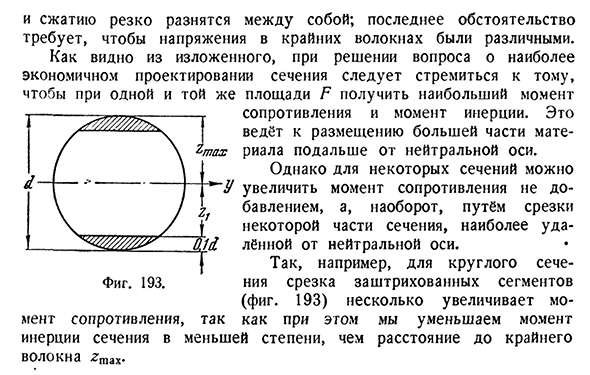
является причиной размещения большей части материала вдали от нейтральной оси. Но некоторые участки не добавляют моментов сопротивления, а, наоборот, увеличивают, отсекая часть наиболее удаленного участка от нейтральной оси. Например, для круглого сечения-разрез затененного сегмента(рис. 193) незначительно увеличивает МО-так как в этом случае мы уменьшаем момент инерции сечения до степени, меньшей расстояния до крайнего волокна GT-A-X.
Смотрите также:

