Оглавление:

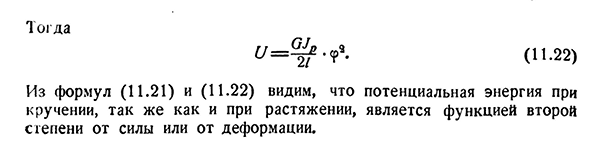

Потенциальная энергия при кручении
- Потенциальная энергия кручения. Выше исследование растяжения показало, что при деформации упругой системы накапливается энергия, которая называется потенциальной энергией деформации(Статья 41). Это явление происходит даже с изюминкой.
Если упругий стержень внутри резинки закручен под определенным углом, то после снятия внешней силы он будет вращаться и работать за счет потенциальной энергии кручения, накопленной в
стержне. Игнорируйте необратимые потери (нагрев, внутреннее трение и др.).), Людмила Фирмаль
Мы должны, таким образом, считать, что работа обнаруженных внутренних сил, определяемая величиной потенциальной энергии деформации u, равна работе внешних сил D. На одном конце закреплен вал, к свободному концу которого приложена пара сил момента, которые постепенно возрастают от нуля до конечного
значения L K. По мере увеличения величины момента пары сил угол кручения SR связывается с уравнением l4k (11.18): Знак/ Если отложить к горизонтальной оси угол оси кручения (деформации) и продольно разместить соответствующую величину крутящего момента на оси, то их взаимозависимость выражается примерно
- наклонной линией. 132). Если повторить вывод, сделанный для вычисления работы силы P при растяжении, то можно увидеть, что работа пары L4K представлена площадью треугольника OAB: l-2. Наличие множителя y в Формуле (11.20) (11.20) обусловлено тем, что момент M K не был сразу применен по его суммарной величине,
а постепенно применялся к его конечному значению. Имеется в виду подставить это значение из уравнения (11.18) вместо CP и получить формулу потенциальной энергии при u=A>twist: «Статический» рост с нуля Я-к — (11.21)2Г ДЖП’ Потенциальная энергия также может быть представлена деформацией
путем замены значения крутящего момента уравнением (11.20) на уравнение (11.18): Gjp202 поворот. Людмила Фирмаль
Проверка прочности[глава XI Затем 6 / =^-<Р3. (11.22)) Формулы (11.21) и (11.22) показывают, что потенциальная энергия кручения и растяжения является функцией силы или деформации вторичного элемента.
Смотрите также:

