Оглавление:















Расчет на удар при осевом действии нагрузки
- Расчет воздействия Под действием осевой нагрузки Явление соударения необходимо рассматривать в том случае, когда скорость рассматриваемого конструктивного элемента или соприкасающихся с ним деталей изменяется на конечную величину за очень короткое время большое ускорение (торможение) в результате чего может привести к значительной инерционной силе, действующей в противоположном направлении. 625 направление ускорения, то есть направление движения тела. В случае падающей нагрузки величина ударной силы (динамическая сила P J может быть рассчитана по следующей формуле (22-1) Падение;7(О перевозке после касатьться ей Ж / 7//. 7 /////л В А Б Рис пятьсот восемьдесят один Где Q-
вес падающего груза, а g-ускорение свободного ускорения падающего препятствия. Однако определение ударной силы РД (/) по формуле (22.1) указывает на то, что время удара, то есть скорость движения движущегося тела от максимального значения в момент контакта с адареальным телом (начало удара), в связи с последними (конец удара) этими трудностями, напряжениями в элементах согласно способу, когда движущееся тело сталкивается, уменьшение их кинетической энергии накопления считается равным увеличению потенциальной энергии деформации сталкивающегося упругого тела. Вывод формулы для определения динамических напряжений осуществляется на примере простейшей системы(рис. 581 изготовлен из вертикально расположенной упругой призмы) Р Р Р Р Р
Я считаю, что это неэластично в том смысле, что это стержень, он не отскакивает от стержня, а движется вместе с ним», и, Людмила Фирмаль
следовательно, в стержне возникают упругие волны и даже эта система имеет некоторую степень свободы. 1) нагрузка Q прикладывается к стержню статически, т. е. нагрузка медленно увеличивается от нуля до максимума(рис. 581, а) и сжимают стержень на величину 6st;2) при падении груза с определенной высоты H ударяют по стержню, создавая в нем сжатие и 6D>6SG(фиг. 581, б). Изменение деформации под действием нагрузки Q ударного воздействия по сравнению с деформацией при статическом приложении той же нагрузки может быть охарактеризовано коэффициентом кинетики б — — (22.2) 626 динамическая деформация вследствие статики может быть представлена выражением 6D=^S CT. (22.3) Если рассматривать линейную зависимость между
напряжением и деформацией, то можно лишь предположить одинаковый модуль упругости при статическом и импульсном действии нагрузки, что подтверждается экспериментами с достаточной точностью.: 1-я=Усть»я (22.4) Куда? В чем же разница? (22.5) — Напряжение, возникающее в стержне при сжатии силой, равной весу падающего груза; Для использования формулы (22.4) необходимо определить динамический коэффициент LD. При этом, исходя из общепринятого в теории удара допущения, соотношение между силой и деформацией остается неизменным, как при статических, так и при динамических нагрузках, то есть при динамических нагрузках. bet=; (22.6) » d=’(22.7), где PCT-статическая нагрузка, равная весу падающего груза(где PCT=Q); p d-сила инерции ударного тела в первый момент контакта со стержнем. Изменение кинетической энергии падающей нагрузки численно равно работе, проделанной ею при падении и деформации стержня: Т-Q(ч+Лю,(22.8) И, учитывая формулу (22.7), потенциальная энергия деформации
- ударного упругого тела, накопленная за счет уменьшения потенциальной энергии падающего тела, рассматривается как сила и деформация. ^д=4RA= = ^—(22-9) Используя закон сохранения энергии, можно игнорировать потери энергии вследствие локальной пластической деформации при столкновении тел, а также инерцию массы пораженного стержня. На основе формулы 627 (22.8) и (22.9) Сы — ^=0(я+Эд). (22.10)) 6ST= — C, уравнение(22.10) можно сделать следующим образом: BD-26ST6D-2bstia=0. Отсюда можно определить динамический вариант: (22 Знак минус этого выражения не соответствует физической стороне рассматриваемой проблемы, поэтому необходимо сохранить знак плюс. Напишите формулу(22.11) следующим образом (22.12) Если сравнить его с формулой (22.3), то получим формулу коэффициента динамизма: (22.13) Учитывая скорость падения груза в начале удара), коэффициент динамичности можно выразить в следующей формуле Запись (22.14) Если
вы подумаете об этом 2 / Y QH тогда 2 4 ″ Потому что он может также написать динамический коэффициент kn: +1 /1 + -^(22.15) Где = QH-кинетическая энергия груза, падающего к моменту удара; UCT-энергия деформации при ударе упругого стержня, которая накапливается со статической силой, равной весу ударного груза Q. (22.16) 628if N■■=0, то есть сила прикладывается внезапно, и тогда, согласно формуле (22.13), коэффициент динамичности 1gl=2. Поскольку высота опускания груза Н всегда значительно больше ставки, то в большинстве случаев определение коэффициента динамичности в уравнении под корневой единицей по сравнению со вторым членом основано на уравнении (22.13).、 (22.17) Или по формуле(22.15)), (22.18) Если мы имеем формулу для коэффициента динамичности (22.13), то напряжение при ударе, исходя из зависимости (22.4),
определяется по формуле — Сгст. (22.19) Или + 22-20. Аналогично определим силу удара: (22.21) Приближенная теория расчета удара имеет Людмила Фирмаль
определенные пределы применения. Они обусловлены скоростью падения нагрузки при ударе и жесткостью конструкции, а-o//y-это формула (22.13) или (22.15) отношения-t — или—Y.-0-это. Ост у БС Так что если Погрешность расчета не превышает 10%. Учитывая массу пораженной структуры, расширяют применение теории приближений. Из анализа уравнений мы видим равные равномерно распределенные напряжения во всех сечениях стержней(22.19) и (22.20)., Величина динамического напряжения, а также площадь F поперечного сечения зависят от величины упругого стержня, подвергаемого большему удару (большей»энергии»стержня), чем ниже динамическое давление., 629 проводит в нем, и чем больше модуль упругости материала стержня, тем больше динамических напряжений генерируется. Ранее предполагалось, что стержни,
подвергнутые удару, имеют одинаковое поперечное сечение по всей длине. Для такого стержня верно все, что говорится о роли объема стержня в оценке динамических напряжений. Изображение несколько отличается в стержне, и некоторые из них имеют разную площадь поперечного сечения. В этом случае (рис. Пятьсот восемьдесят два, Ф-l1X1 К-71 1×1 ТСС./ а б Рис пятьсот восемьдесят два Как В а)самое высокое номинальное напряжение Полюса (за исключением концентрации) находится на самом малом участке(в месте вращения). Это зависит, как известно, от способности деформировать весь стержень, а не только его слабые части. В этом случае динамическое напряжение вызывается увеличением поперечного сечения участка углубления или уменьшением площади поперечного сечения утолщения стержня, и таким образом, когда
весь стержень определенного диаметра всего стержня равен диаметру углубления d2, деформируемость стержня значительно повышается, что приводит к уменьшению динамического напряжения СД. Таким образом, снижение напряжений при ударе может быть достигнуто за счет увеличения объема за счет устранения утечки, то есть за счет изменения объема различных материалов. Вышеизложенное просто иллюстрируется примером определения максимального динамического напряжения, возникающего в трех видах стержней, имеющих продольное воздействие грузом Q, падающим с одной и той же высоты H. Соотношение между отдельными размерами стержней выглядит следующим образом: Г«/2О Чтобы определить напряжение каждого стержня, используйте общую формулу (^Д)Макс=(ССТ)Макс=^Д~~Е «’ мин. 1+6^ ’Энф Н Куда? LD=1H-и-число шагов. Для ступенчатых стержней (рис. 582, а) Для стержня определенного поперечного сечения с размерами утолщенной части ступенчатого стержня (рис. 582, б) (6ст) б=. Для стержня с постоянным поперечным
сечением, равным минимальному поперечному сечению ступенчатого стержня (рис. 582, в), мы имеем ((Оды’ \ — ул В ) — (^St) a: (BST)b’•(6st)»-P4:1:•(22.22)по сравнению с корнем (22.17) игнорируя формулу единицы, которую можно принять с высокой высотой падения H и малой статической деформацией 6SG, с коэффициентом изменения. Используя эту формулу и принимая во внимание формулу (22.22), получаем зависимость между динамическими коэффициентами рассматриваемых случаев: (M»: (MS••(M. =V In (1-P) N: 1:<22-23) на основе формулы (а г)=(а СТ), А==(^Г)=(^Л)и> (д)б=(ЛД)б((ТСТ)Б=;(Д) Е=(^Д)в (СТ)|А Р::•(22.24) Например, предположим, что коэффициенты a и P имеют следующие значения: «=^ — =0,5; p=A — =0>4 — Г11 631 выражение (22.24) находим в следующем соотношении: (ad)«: (SGD) b: (od) b=1,7:1:1,41. Поэтому видно, что максимальное
напряжение возникает в стержне, имеющем углубление(фиг. 582, а), причем наименьшие находятся в стержнях определенного максимального сечения(рис. 582, б). В том же минимальном поперечном сечении стержня длина постоянна (рис. 582, в), напряжение имеет промежуточное значение. Результаты анализа имеют практическое значение. Прежде всего, этот анализ показывает, что характер сопротивления стержней ударам качественно отличается от сопротивления их статическим нагрузкам. При плотном сжатии утолщение части стержня не вызывает изменения напряжения части другой части. Локальное уменьшение площади поперечного сечения при небольшой длине стержня резко повышает давление. Для уменьшения напряжений, для получения всех частей стержня с одинаковой минимальной площад
ью поперечного сечения, необходимо увеличить податливость стержня, добавить буферную пружину, разместить материал с разным модулем упругости, а следовательно, для проектирования стержня и устранения удара, необходимо добиться определенной площади поперечного сечения по всей длине. Локальные утолщения допускаются только на небольших участках длины, а локальные впадины в небольших диапазонах крайне нежелательны. Если при таких условиях не удается построить достаточно прочный стержень, необходимо его удлинить или равномерно увеличить его площадь. Условия ударной прочности следующие (Компакт-диск)Макс [компакт-диск 1=’ • Поскольку динамизм уже отражен в Формуле коэффициентом KB, то значение запаса прочности PT выбирается равным значению основного запаса прочности (1,4-1,6) при работе
на статической нагрузке. Данная работа посвящена расчету динамических напряжений в случае ударного сжатия. Однако все вышеперечисленные формулы, особенно в случае, как показано на рисунке, также эффективны для ударного растяжения. Пятьсот восемьдесят три Рис пятьсот восемьдесят три Поперечное сечение Например 92. Прикрепите Q с весом 5kge к стальной проволоке диаметром 3 мм(рис. 584), свободен. Найти напряжение провода, когда его верхний край внезапно останавливается. Массу можно игнорировать. 632напряжение точки А после внезапной остановки провода попадает в уравнение (22.20) при длине провода/=N: «Q<1/2QHE4-5,Give/4•2. 5 — 2,1 • 10* F+V ~ fT~l. 0.3’+V=(70,8+17,200) кгс / см2 17,271 кгс / см2. Поскольку кинетическая энергия падающего тела возрастает с той же скоростью, что и объем провода, напряжение не зависит от высоты снижения нагрузки Q. Пример 93. Определит
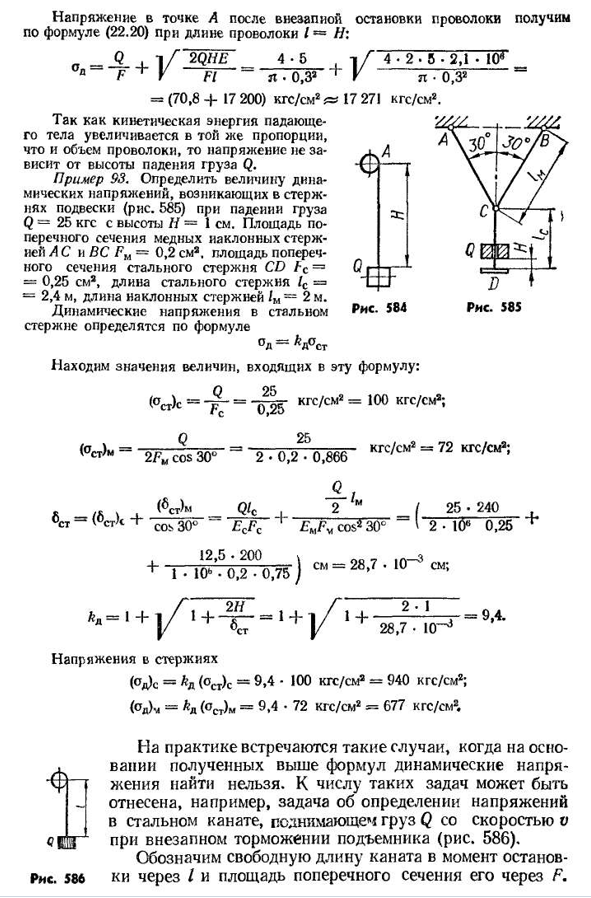
е величину динамического напряжения, создаваемого в стержне подвески (фиг. 585) при падении груза Q=1KGE с высоты H-25 см. Площадь поперечного сечения медного наклонного стержня AC и BC FM=0,2 см2. Какова площадь поперечного сечения стального стержня CD? s= = 0,25 СМА, длина стального стержня 1С=2,4 м, длина наклонного стержня/м=2 м. Динамическое напряжение стального стержня определяется по формуле°d-V ct, а величина количества, содержащегося в этом уравнении, определяется: Около 25 <А Ст)Ы=и н ы-г С/С м2=1 0 0-г С/С м2; (ПС т) м Q 2fm минимальный заказ cos30° Двадцать пять 2 • 0,2 • 0,866 кгс / см2=72 кгс / см2; L/л i_Qlc. 2 / m_ / 25 * 240 И CZ (G * EU RS’COS ’30°’ 2•l (>0,25 1+J В/Е-1+ — 9л Напряжение в стержне (ОД) ы=ЛД (ост) ь=9.4-100kgf/см2=940kgf / см2; (ОД) м=ЛД (Ост) м=9.4•72kgf/см2= = 677kgf / см2. Ф-[EG1 Рис пятьсот восемьдесят шесть На практике встречаются случаи, когда динамические напряжения не могут быть найдены, исходя из приведенной выше
формулы. Среди таких задач, например, задача определения напряжения стального каната, поднимающего груз Q со скоростью v при резком торможении подъемника (рис. 586). Обозначим свободную длину каната в момент остановки через I и площадь его поперечного сечения через L. Он основан на законе сохранения энергии, согласно которому, игнорируя массу кабеля, кинетическая энергия движущейся нагрузки полностью преобразуется в потенциальную энергию деформации кабеля.: <2»®, Мне 2/ — — 2 Ф — = — ^-+М (6-М » Где и что иметь в виду М=е — ^ — т получить 21(8°8C T) 2—2g • И так оно и есть. 6-ставку+у В результате, при внезапной остановке, растягивающее напряжение возрастает до EFg V=1+^9(22.25) То есть к.=1+. д Пример 94. Определить напряжение на стальном канате Нижнего q=1TC со скоростью 1 м/с, если внезапн
о остановится при падении нагрузки на 4 м. Канат F=16 см2; модуль упругости£ = 1,5*10E Рассчитайте статическую деформацию каната: икс =■Q>/ = 1,40550 •0 1•0 *1 8■ 0106 cm=°_ ’ 4L o8p2m коэффициент динамичности, согласно формуле (22 25) £d=14-=1+G100 — =5>6 G H t£G0. 482-981 И динамическое напряжение тока °д=*д°ст= — у=°. О-Джей г Высокое напряжение, возникающее при резком торможении, может привести к обрыву подъемного троса, что необходимо учитывать. Пример 95. Для решения предыдущей задачи, если между Канатом и грузом поместить пружину, то под действием нагрузки 4500КГЭ дает статическое растяжение 12 см. Статическая деформация упругих элементов (троса и пружины 6«т)) 6ST= = (°>4 8 2 + 12> s m=1 2’4 8 2s m — «5,6 кгс / см2=1575 кгс / см2. 634 ставим значение 6^в выражение (22.25), находим его Л д= 1+_^=. =. −100. Динамическое
натяжение каната В 1 4—г -. = — =1.92. / 12 482 ■ 981 Четыре тысячи пятьсот; d » y-I>92-y кгс / см2=540 кгс / см2; Как видим, включение пружины между тросом и грузом значительно снизило динамическое напряжение при быстром торможении груза (почти в 3 раза). В этом случае пружина является амортизатором удара, который часто используется в технике для смягчения удара, и поэтому уменьшает динамические напряжения, возникающие при ударе. Рисунок * 587 Это объясняет массу стержня, испытывающего удар. В некоторых случаях вес стержня может существенно влиять на динамические
напряжения, возникающие в стержне, подвергнутом ударным нагрузкам. Чтобы рассмотреть влияние инерции массы пораженного стержня в процессе удара, необходимо различать два этапа: первый начинается с момента его касания падающим грузом с максимальной скоростью, а конец стержня, когда произойдет дробление материала, имеет значение скорости и верхнего конца. В начале второй стадии удара, если верхняя кромка пораженного стержня имеет скорость vlt, скорость последующего (нижнего)участка стержня линейно уменьшается, и rots 587) в этот момент скорость удара уменьшается.: Г(х)= — г -. Кинетическая энергия массы участка dx, стоящего x от нижнего конца, Тогда полная кинетическая энергия является формулой Находится в РАН- Палку определяется Дж’% Показывая собственный вес стержня через Qt, кинетическая энергия первой ступени второй ступени может быть выражена формулой Т4).)
Поэтому, если в момент начала первой ступени удара падающая нагрузка обладает кинетической энергией, то потеря энергии перед началом второй ступени обусловлена локальной пластической деформацией. Л * Г Г°З (я, КК^я\ \ 2г+3 2г/’ Или 4Г — +<22-27′ С другой стороны, при потере той же кинетической энергии, кинетическая энергия падающей нагрузки уменьшается на величину (v-y-j2) V-vlt удара для первой ступени быстрого удара нагрузки в первой ступени удара пораженный стержень получает запас кинетической энергии, а затем потери энергии падающего стержня уменьшаются., Или At=[U2-2uu,+u| (1 + -|-4)] • (22>28) Если мы приравняем правильную часть выражения (22.27) к (22.28 — ?(> + 4-«] — 4 (’+4->)] • Отсюда определим величину скорости движения груза в начале второго этапа удара: (22.29) Энергия удара стержня, характеризуемая кинетической энергией, накопленной системой в первый момент второй ступени удара, определяется по формуле. (22.30) Т удара по закону сохранения энергии и преобразования в потенциальную энергию деформации
упругого стержня. Поэтому полученную формулу (22.30) и Формулу (22.15) следует заменить на те, то есть определить коэффициент динамичности. Или П2. Если указать-H и HQ=Then, а также -=== — p, то формула для определения коэффициента динамичности имеет вид Или максимальное давление на стержень, испытывающий воздействие, Из последней формулы следует, что если значение коэффициента Р (отношение веса к падающей нагрузке пораженного стержня) не мало、 (22.31) по сравнению с блоком энергия удара t=-2^т. е. с учетом массы стержня расчетное напряжение при ударе уменьшается. Удар палкой о твердую пластину. В некоторых случаях необходимо определить напряжение ударяющего органа, особенно
путем расчета стержней кованых Молотков. В то же время, наиболее опасен для прочности стержень Рис пятьсот восемьдесят восемь Это момент окончания ковки, когда кованое изделие практически не деформируется, а вся энергия удара поглощается стержнем. В этом случае она схематично показана на рисунке. 588, длина поперечного сечения F и масса Q некоторых призматических стержней I падают с высоты II и ударяются о жесткую пластину A. поскольку пластина не деформируется, в момент столкновения Так как природа сил инерции массы (они действуют на каждую единицу объема) различна, то стержни имеют разные размеры при ударе о пластину с каждым участком динамического напряжения. В верхнем сечении они равны нулю и увеличиваются по последующему (нижнему)
линейному закону, достигая максимума в нижнем сечении. Динамическое напряжение при любом поперечном сечении стержня х(рис. 589)по самому высокому напряжению нижней секции можно выразить как: ОД (%)=(ОД)максимум~ • Величина потенциальной энергии деформации под действием силы инерции в стержневом элементе dx может быть выражена как dU= — °fl (x) Fdx=(D / max-y pi~y pi (22.35) из сравнения уравнений(22.35) и(22.20), игнорируя последний член—, мы можем видеть, что динамическое напряжение ударного стержня является проблемной породой, она падает на твердую пластину.
Смотрите также:
| Расчет на прочность при повторно-переменных напряжениях | Напряжения при скручивающем ударе |
| Понятие о малоцикловой усталости материалов | Расчет на удар при изгибе |

