Оглавление:










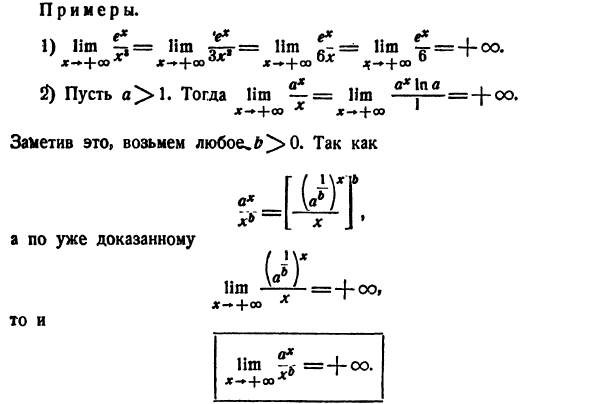


Основные теоремы дифференциального исчисления
- Основные теоремы дифференциального исчисления Н°1.Роль theorem. In в этом разделе мы устанавливаем некоторые важные теоремы. Начнем с теоремы, принадлежащей французскому математику роллу [M. Rolle, 1652-1719]. Пусть теорема f (x) является гладкой) функцией на интервале[a, b].Если / 00 = 0、/()= 0、 Тогда между a и B. должна
быть по крайней мере 1 точка c (a 0 и пусть x * — значение аргумента f (a)= f (b)= 0, x не соответствует ни A, ни B%, поэтому x (рис. 172) а <х <б. Так, функция сглаживания f (x) принимает минимальное значение m во внутренней точке отрезка[a, b] 9.То есть функция в точке x *есть (сглаживание!) Имеет минимальное значение, и согласно принципу ферма, f (x *) = 0.So, x * — обязательная точка c. теорема доказана.
X. F (х*) = м. }(х *)= ТФ 0, а точки A и 1к поскольку Людмила Фирмаль
н°2.Формула конечного приращения Теорема Лагранжа. Если интервалу[a, b]задана гладкая функция f (x), то между a и B. должна быть хотя бы 1 такая точка c (a )-г(о) Это называется обобщенным конечно-инкрементным выражением или выражением Коши. Доказательство. Ввести вспомогательные функции Ф(Х)= \ /(Х) — ф(а)] [г(ь)-Г(А)] — \ Ф(б) — ф (А) — Ф (А)] [Г(х) — г(а)]. Эта функция и ее производные Ф(Х)= ф (х) бревна(Б)-Г(А)\ -\ Ф(Б) — /(А)] Г(х \
Непрерывный. Непосредственно из Формулы φ (q) видно, что φ(σ)= 0 и jf(b)= 0.Таким образом, условие теоремы о роли выполнено, так что между a и b<| / ©= 0, или то же самое * ) А. Л. Коши (1789-1857) — известный математик Франции. Самый Г©[г(ь)-Г(А)} — \ Ф(б) — ф(а)#<)= 0 Отсюда Р©[г(ь)-Г(А))= \ Ф(б)-/(я)] Г(с) И*) F©)_ /( «)-/(«)
- Ж Г(Б) — G(а)• Это доказывает теорему. Замечание. Если написать обобщенное выражение с конечными приращениями для частного случая=, то получится следующая форма: Ф(б) — ф (а) АF©б-в «’ То есть он превращается в регулярное выражение с конечными
приращениями. в N°4.Признаки функционирования гомеостаза. Если функция является постоянной, вы знаете, что ее производная равна нулю. Верно и обратное. Предположим, что теорема f(jc) дана[a, b]и имеет производную f (x). для каждого x из [a, b], если окажется, что f ’(x) равно нулю, можно поспорить: F(х) = const и Доказательство. Выберите точку x из сегмента[a, b], чтобы изменить теорему
a \ x и a \ X. Но в[о, б].То есть f ’®= 0, поэтому、 Ф(Х) — ф(а) Людмила Фирмаль
Лагранжа на сегмент[a. вы также можете использовать ее для этой теоремы, r существует между х-а ’ Или f (x)-F (a)= 0 и f ( * ) = f (a), и поскольку x произвольно, теорема доказана. Образцы. .- И cp (jc)= arc sin jc +
arccos x. И затем… ГВС г \ — Х1 УГ ^ х * ( * ) Этот переход определяется как g ’© 0 0 и g(b) — g (a) 0. Допустимо только для 0.Поэтому необходимо дополнить описание более строгой теоремой, чтобы указанные неравенства были гарантированы. Отложи его в сторону. л Итак,
=0,©= 0. Если отношение производных ограничено (конечное или бесконечное) Ил-fghбыл В этом случае отношение самой функции будет тем же самым пределом. е. /()_ Ля г(х) х-а F(х)
Доказательство. F (a)= g (a)= 0, поэтому дробь Вы можете написать: /()-/()-/(г) с — J£^ Рисунок 174. благодаря обобщенной формуле конечных приращений между a и x всегда существуют следующие точки r: /(*)-/())((икс) Значение г(х) — г? Ж К ’ Кроме того,
Z находится между A и X (рис. 174). ♦ ) Г.-Ф. дехоспиталь(1661-1704). Тогда дробь в виде x-a представляет неопределенность g Ноль — Г * формат x становится a, z становится a, и гипотезы теоремы Г ’ (Z) при Затем по(1) / ( * ) _ л Это доказывает теорему. Образцы. jc» — 7JC +
10.. 2×7 3 1) Лим-г = ПШ =—м -. x — * ^ −4 x-2 4 och и y ^ y-z 1} 2 / x + 7 1 2) 11 M r 7 9 — = lim r ^ =7Γ. ЛК Эйн ’ младший-sfnffl,, 2 грех xsoe х. 3)Лим-г — = Лим-Ф — = 2а грех, потому что сл х — + А * — Ина x_a Икс.. X-грех * .. 1-COS X » SinAT .. потому что:1 4) Лим— = Лим-= 1им = Лим —СС ^. х — + 0 * » ж-О6 * З-О Б 6 Замечание. Неопределенность формы может
оказаться столь же очевидной. Образцы. е * е * е * е * 1) Лим-Джей = Лим а-р = МПС = = ИТ — ^ — = + 00 я)> 1.Лира — = Лим°*!НГ = — 4-00. ДжейТи-4-00 * х-ФОО 1 Теперь, когда вы заметили это, используйте^ & > 0.С б-л-Дж ’ Но уже доказано (b)i lim Ao_ = + oo、 ДГ — Ф-ОО л И То есть экспоненциальная функция растет быстрее
степени. в N°6.Оцените точность уравнения Ay = dy. Раздел.[a, b] L. предположим, что ana имеет функцию/ (•) с последовательными f ’( * * ) и f» ().По формуле Лагранжа Д / (О)= Ф (О + Д)- исправление.) = Γ(х) ВХ. Х между Х9 и Х <//(•)= / ’(#)Ля.* Отсюда А / (о)-ДФ(х.(А) = [/’(Дж.?)-
/(e) 1 вторичное применение формулы Лагранжа、 М-L *)= / *(*) Где hp находится между x и I. Д /(dgv)-д /(х0)= F ’(х»)(-х0) Д *. Укажите максимальное значение в M| f (x). \ X-затем замените dgv на x, чтобы сделать его проще、 К рейтингу Об этом говорится в § 4(I°5).
Смотрите также:
| Производные и дифференциалы высших порядков | Формула Тейлора |
| Исследование функций | Касательная и нормаль |

