Оглавление:







Напряжения в осесимметричной оболочке
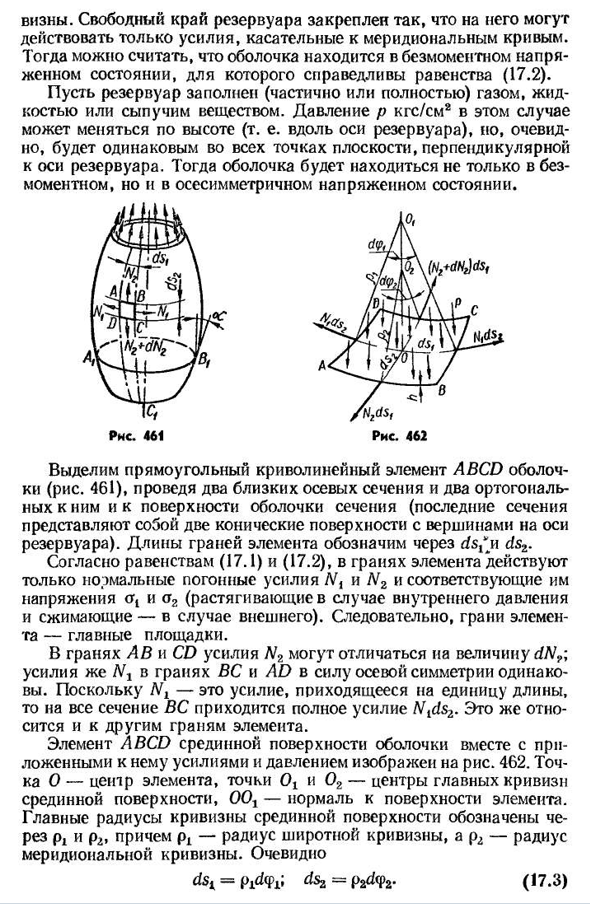
- Осесимметричное напряжение оболочки Рассмотрим резервуар(рис. 461) представляет собой осесимметричную оболочку. В нем меридиональное сечение срединной плоскости образует плавную кривую, которая не нарушается. Предполагается, что толщина оболочки, h, меньше радиуса CRI- 468-это бесплатно.
Свободный конец резервуара закреплен таким образом, что действуют только силы, касательные к Меридианной кривой. Тогда можно предположить, что оболочка находится в безмоментном напряженном состоянии (17.2), где справедливо равенство. Заполните резервуар газом, жидкостью или сыпучим веществом (частично или полностью). Давление Р кгс / см2
в этом случае может быть различным по высоте (т. е. вдоль оси бака), но очевидно одинаковым Людмила Фирмаль
во всех точках плоскости, перпендикулярной оси бака. Выделите прямоугольный изогнутый элемент ABCD shell(рис. 461), имеет два близких осевых сечения и два ортогональных к ним и на поверхности оболочки сечения(последнее сечение является длиной плоскости двух конических элементов, имеющих вершины на оси резервуара обозначается ds^n ds2. Согласно уравнениям (17.1) и(17.2), обычные линейные силы n t и N2 и соответствующие им напряжения SG (и O2
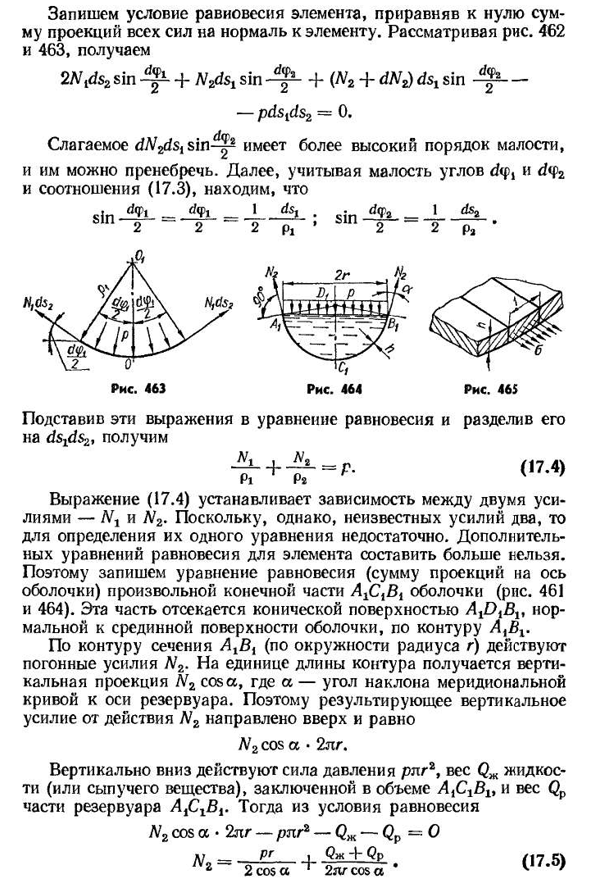
(для расширения и сжатия—внешние), следовательно, плоскость элемента является основным участком. С точки зрения AB и CD, мощность Nz равна d (V? Сила N-l в плоскости BC и AD из-за осевой симметрии одинакова. Поскольку Nt-это сила на единицу длины, то суммарная сила nlds2 падает на всю Солнечную секцию-приложенная к другим плоскостям того же элемента. Элемент ABCD средней поверхности оболочки вместе с приложенными к нему силой
- и давлением показан на рисунке. 462 точка O-это центр элемента, вы указываете его? — Центр основной кривизны срединной плоскости, ООГ-перпендикулярно поверхности элемента. Главный радиус кривизны срединной поверхности обозначается RL и P2, где RL-радиус Широтной кривизны, а P2-радиус кривизны Север-Юг. Очевидно, ds4=p1d7.11)первая, третья и четвертая теории прочности условия прочности приведены в виде (Tskbiv= — § — ;ч=младший(costp-КГУ); п-УН-г (с COS<Р-КГУ). Из уравнения Лапласа следует+° / = — T — =T (COS f-C0SΦ). Теперь воспользуемся уравнением (17.9). Значение<2J равно весу жидкости в объеме шара, диаметр сегмента: QK=tVacb=T-n
f c (3R-Yas)-высота шара сегмента HC-7?(1-costp). И так оно и есть. 0 ватт= — г-Р3(1-соѕ Ф) 2(2-й-потому что Ф). Если вы присвоите выражение (17.9) выражению p, g,<2J, a и проигнорируете вес резервуара Qp, то получите следующее выражение п Г1+с COS<Р+cosg<Р соз Р1 / 1 7 141 ч[3(л -) — потому что<Дж>)2Д(1 7.1 5 ) 473i л 2cos2f+2cos f-1 3(1+cos f) (17.16) Максимальное значение напряжения получается в точке C, где, зона p=0. Учитывая P, = PT=R, из уравнения Лапласа получить дополнительное уравнение°t+a t= = — yR COS f. (17.19) для вычисления веса Диа-части пласта: Qp=I^ACB-yhSACB,
где площадь наружной поверхности Sacb шарового сегмента ACB —%n. RHc=2l/?а Людмила Фирмаль
(1-соз Ф). Значение, Qп-2 nyrhr2(1-е КС). Теперь подставим формулу Qp и G=R sin f в Формулу (17.9); a=90°-f; p-0 и примем во внимание, что вес детали DIA в сечении AB вызывает сжатие.、 Год Я+соѕ Ф (17.20 )) Тогда уравнение (17.19) (17.21) Напряжение Север-Юг уплотняется повсюду, увеличиваясь на расстоянии от верхнего края купола до края. Кольцевое напряжение
Смотрите также:
| Расчет вращающихся дисков | Распорные кольца в оболочках |
| Элементы теории тонкостенных оболочек Введение | Краевая задача для тонкой цилиндрической оболочки |

