Оглавление:




Потенциальная энергия деформации
- Потенциальная энергия деформации Согласно закону сохранения энергии, работа внешних сил не исчезает, а преобразуется в потенциальную энергию, накопленную в упругом теле. Таким образом, величина кумулятивной потенциальной энергии деформации определяется величиной работы внешней силы. Эта энергия, проявленная в виде работы, должна была разгрузить
внутренние войска. Снимая, например, часть груза, прикрепленного к балке (рис. 385), отметив, что балка выпрямилась и осталась целой. Таким образом, упругое тело может накапливать механическую энергию, которая может быть возвращена при разгрузке. Игнорируйте изменение кинетической энергии системы
при статических нагрузках и потери энергии из-за внутреннего трения, изменения температуры, магнитных и электрических явлений, Людмила Фирмаль
возникающих при деформации! Энергия нагрузки равна потенциальной энергии деформации, накопленной упругой структурой. И=вверх, (13.66) amde U-это приращение потенциальной энергии преобразования. Уменьшение потенциальной энергии нагрузки численно равно работе внешних сил при нагружении объекта. Таким образом, потенциальная энергия деформации
численно равна работе внешней силы при нагружении системы или внутренней силы, совершаемой в процессе разгрузки. Уравнение (13.22) на основе пучка l1f, 1S, 1f L’gkr^,-2J EJy f 2j EJZ2JJ s gjk s S S S S В общем случае энергии потенциальной деформации 1 этаж,#ДС, 1Ф J в М^ДС +2] эф+2Д 2Д к Г С с (13.67)) Как видно из этой формулы, потенциальная энергия искажения является квадратичной функцией обобщенной силы или обобщенного смещения. Поэтому
- потенциальная энергия деформации всегда положительна. Его величина не зависит от порядка нагрузки, она полностью определяется конечным значением силы и перемещения. Также отмечается, что потенциальная энергия как функция второго порядка обобщенной нагрузки не следует принципу независимости действия силы. Предполагается, что накопленная потенциальная энергия в результате действия группы сил, суммарная потенциальная энергия, вызванная действием каждой нагрузки, сила движения
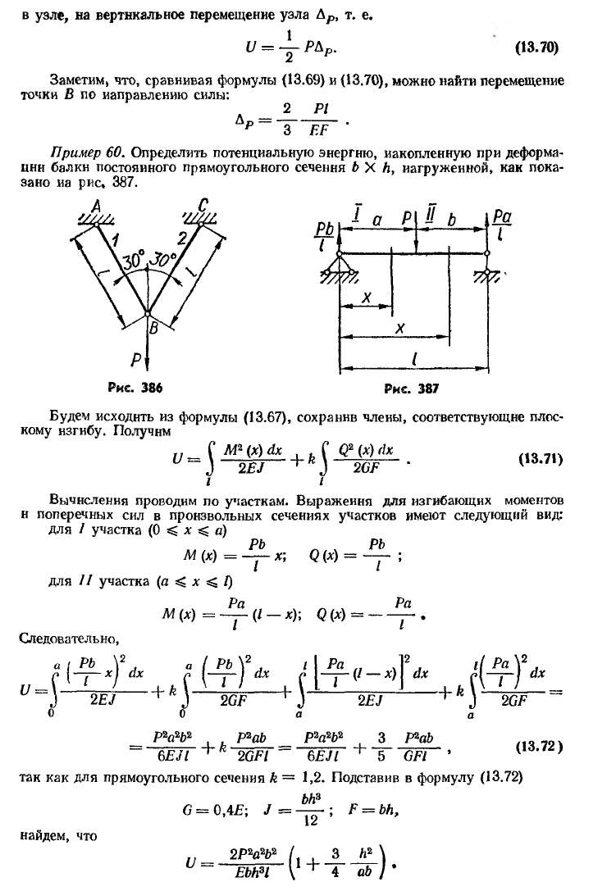
в направлении одной обобщенной силы, вызванная действием другой силы, является законом независимости действия силы при расчете нагрузки. Пример 59. Определите величину потенциальной энергии деформации, накопленной в шарнирной стержневой системе (рис. 386), стержни AB и BC, нагруженные в узлы вертикальной силой R, имеют одинаковые размеры и изготовлены из одного и того же материала. Рассматривая равновесие узла B, мы видим, что стержень растягивается с той же силой: (13.68) Следовательно, потенциальная энергия деформации системы (13.69))
С другой стороны, исходя из Формулы (13.10), потенциальная энергия искажения может быть выражена как половина произведения Людмила Фирмаль
приложенной силы Тринадцать.* 387b узел, Dr в вертикальном движении узла, I = — R B R. 03.70) заметим, что сравнивая уравнения (13.69)и(13.70), можно найти движение точки B в направлении действия силы: 2Р! L₽_ _ 3 ″ F. F» Например, 60. Получена потенциальная энергия, накопленная при деформации балки неподвижного прямоугольного сечения B×L. 387. Мы исходим из Формулы (13.67), сохраняя члены, соответствующие плоскому изгибу. Возьми (С (13.71) J26F Один. Расчет осуществляется на месте. Формула для изгибающего момента и силы сдвига в любом участке участка равна / plot(Oh, Oh, Oh, Oh) ) 7 и(x)=U график z(a<x /) М(Х)=~(I-х); м(х)= Р(х);м(х)= ; Для: Эдевальд, РА-г — /И РА п. и Два. е! J2GF х * j2e
все GL a2y2t p*ab P2a2b2 3R-6EJI+K2GFI-GEM+5GFI ’ L=1,2 для прямоугольного сечения. Присвоить выражению (13.72) 6=0.4£;^= * л, 2EJ2GF2GF (13.72) / Найти ее п 2P * o нет. «Ebh*л» (|+т у )- 388½ ’ последних членов в скобках, чтобы выразить влияние сдвиговых сил на нормальный размер балки, не превышают 2-3%. В связи с этим при изгибе балки влияние поперечных сил при расчете потенциальной энергии обычно игнорируется. Чтобы рассчитать отклонение балки в точке приложения нагрузки, представим потенциальную энергию деформации балки как 1/=4, DDR(13.73), и сравним уравнение (13.73) n(13.72).、: К Ноги (13.74)
Смотрите также:
| Вычисление интегралов мора по способу верещагина | Теорема Кастильяно. теорема Лагранжа |
| Применение способа верещагина к стержням переменного сечения | Теорема о минимуме потенциальной энергии |

