Оглавление:


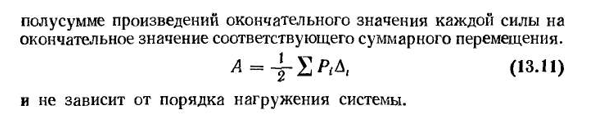

Работа внешних сил
- Работа внешней силы Когда структура деформируется, ее различные точки перемещаются. Точка действия внешней силы также перемещается. В результате работают внешние силы. Вычислим
работу нескольких обобщенных сил P, приложенных к любой упругой линейной деформационной системе (рис. 354, а).
Предполагается, что нагрузка увеличивается от нуля до заданного значения достаточно Людмила Фирмаль
медленно, чтобы инерционная сила движущейся массы игнорировалась. Эта нагрузка, как говорят, менее статична. 362-я сила P в этот момент соответствует обобщенному перемещению D. очевидно, что основная работа внешней силы, игнорируя бесконечно малую квадратичную, равна dA=(P+dP) db^P d&. Полная работа,
достигаемая обобщенной силой P, приложенной к статике, которая вызвала общее смещение D, l=J MD. Но Интеграл(13.8) представляет собой площадь Р-диаграммы заданной структуры(рис. 354, б). В линейной деформируемой системе смещение пропорционально величине силы (закон крюка): D=P6pr(13.9), где BPR-смещение, вызванное силой P = 1. Различают формулу (13.9): dA=DPPP.
- Подставляя полученную формулу в Формулу (13.8)、 п А=6пп Дж Прпр=6 Два. Учитывая формулу (13.9), мы, наконец, получаем l_#RL 2 ′ 2•(13.10) Таким образом, фактическая работа при статическом действии обобщенной силы на упругую систему составляет половину произведения конечного значения силы на конечное значение
соответствующего обобщенного перемещения (теорема Клапейрона). В случае статического воздействия на упругую систему некоторых обобщенных сил (рис. 355) Р Р2,…Работа деформации»P» равна
163 сумма половины произведения конечного значения каждой силы Людмила Фирмаль
на конечное значение соответствующего полного перемещения. л=(, Z и P) и не зависит от порядка загрузки системы.
Смотрите также:
| Изгиб с кручением | Работа внутренних сил |
| Обобщенные силы и перемещения | Применение начала возможных перемещений к упругим системам |

