Оглавление:






Кручение стержней некруглого сечения
- Кручение стержней некруглого сечения В практике машиностроения стержни с прямоугольным, треугольным, овальным и другими сечениями часто подвергаются кручению. В этих случаях гипотеза плоского сечения неприменима, так как сечение является криволинейным (обедненным). Точный расчет стержня некруглого сечения может быть получен методом теории упругости. Однако изложить их в этом курсе невозможно, поэтому здесь мы покажем
лишь некоторые окончательные результаты. Следует отметить, что в стержне произвольного сечения, как и в стержне круглого сечения, тангенциальное напряжение в момент кручения направлено тангенциально к контуру. Максимальные касательные напряжения, линейные и все-крутильные углы по аналогии с кручением стержня круглого сечения определяются по формуле (9.28)) 219(9.29)
Здесь JK и WK — это некоторые геометрические свойства, условно называемые моментом инерции при кручении и моментом Людмила Фирмаль
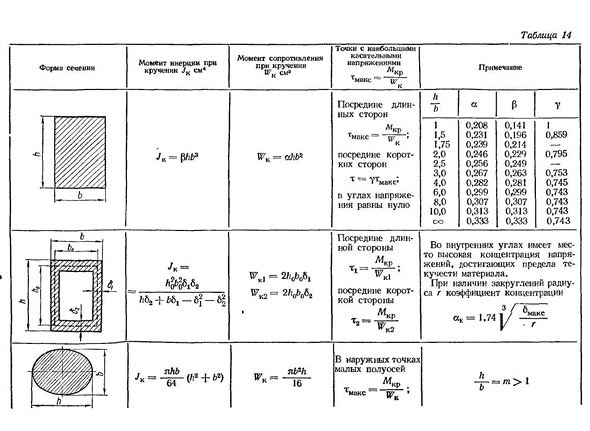
сопротивления при кручении cm4 и cm2. Наиболее распространен стержень прямоугольного сечения. В этом случае распределение касательного напряжения показано на рисунке. 213. Наибольшее напряжение возникает на поверхности в середине (точка С и точка D) длинной стороны прямоугольного сечения. Они определяются по формуле (9.28), где 1WK=ahb(9.31) h—длинная сторона
прямоугольного сечения. Б-его короткие стороны. Напряжения (в точках А и в), возникающие на поверхности среднего участка короткой стороны, следующие. T=utmax-(9.32) принимает JK=fihb3 для определения относительного угла кручения прямоугольного сечения в уравнении (9.29). — (9.33) коэффициенты A, Y и 0, в зависимости от соотношения, приведены в таблице. 14. Имеются также данные о скручивании некоторых других некруглых участков. Запишите условия прочности и жесткости прямоугольного сечения: Тмакс —
- (9.34)) (9.35 утра )) При скручивании стержня с формой равнобедренного треугольника, путем вычисления стержня с эквивалентным прямоугольным поперечным сечением, приближенные значения максимального касательного напряжения и угла кручения последнего строятся следующим образом. 214): от центра тяжести от трапеции перпендикуляры SV и CD опускаются в сторону, а затем Прово- 22Г Полученный прямоугольник представляет собой эквивалентную площадь поперечного сечения рассматриваемого трапециевидного стержня, и следует применять формулу (9.28)—(9.33). При кручении стержня с эллиптическим
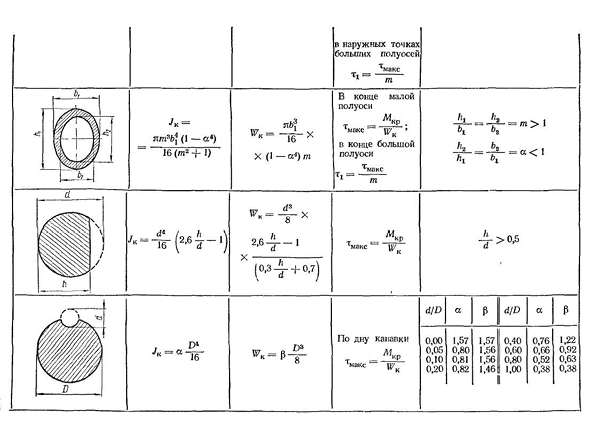
сечением максимальное тангенциальное давление составляет малую полуось (рис.215) происходит в крайней точке, которая в данном случае P7_ _ nb2fl 16′ Где B и H-размеры малой и большой осей эллипса, соответственно. Максимальное напряжение в точке наружного поперечного сечения основного диаметра Л Где M= — y-крутящий момент инерции эллипса J K=(L2+B2). (9.36 утра)) Значения для JK и некоторых некруглых поперечных сечений приведены в таблице. 14. JK=J4 «AZ для него, если стержень представляет собой сложную открытую закрутку, которую можно разделить на части C и WKl+ • • • 4»?KP=2KP, где/=1;2; 3;…;n — числа в простейшей части раздела разбиты. Потому что угол скручивания для всего сечения и всех деталей одинаков: _ ^К Р^КР1_ _ «г ЖК-6ДЖ К1»GJK Н> Крутящий момент пропорционально распределяется между отдельными секциями пропорционально жесткости: L4cr1=;L1cr2=L4cr у»• * * * >
=М СГ т * ■ ’ с Таким образом, максимальное касательное напряжение Людмила Фирмаль
каждой части ( / ) сечения футболка= Т Макс~7г~’ Раздел,(9.37) Который • • • Части ХН ^КР£^К Р|\J в КЛ ’ 1. Л1 ″ Р1! Зки \ ^К 1I-JK1 Максимальное значение напряжения t достигает для элемента 77/7-K1 ■ б Y7K1=2 / ^D == Т1= Примечание ч б Но серебро Y 1 0.208 0.141 1 1,5 0,231 0,196 0,859 1,75 0,214 0,239 2,0 0,246 0,229 0,795 2,5 0,256 0,249 — 3,0 0,267 0,263 0,753 4,0 0,282 0,281 0,745 6,0 0,299 0f299 0,743 8,0 0,307 0,307 0,743 10.0 0.313 0.313 0.743 SS 0,33333 0,743 во внутреннем углу представляет собой высокую концентрацию давления, достигающую предела текучести материала. При наличии радиуса округления G коэффициент концентрации зет ■°Max на наружной точке большой оси ^макс Тонны В конце малой оси т. В конце большой оси М YKS ПЕЧАТНЫЙ ШПУНТОВАЛЬНЫЙ СТАНОК Т Макс Cr ШК М Т Макс ^2^2 Ч±БТ =а<1 кр
. В нижней части паза д/д А↔Д / Д↔ 0.00 0,05 0.10 0.20 1,57 0.80 0.81 0.82 1,57 1.56 Тысяча, пятьсот, шестьсот, одиннадцать 1.46 0.40 0.60 0.80 Из 1.00 0.76 0.66 0.52 0.38 1,22 0.92 0.63 0.38 где Пример 31. Если известно, что стальные стержни с прямоугольным поперечным сечением подвергаются допустимому напряжению кручения[t] — 400 кгс / см, то передают крутящий момент L4K= = 100 кгс * м и находят размеры поперечного сечения стержня? И об отношении партии −2.5. От требований прочности М КР. Т Макс 1T1 Найти момент сопротивления скручиванию стержня: M1t10 000 9LG I!£__==- ТГЛ-см=25cm3, (t) 4, 0, 0. д а, знать соотношение сторон сечения — =2,5 и брать из таблицы. 14 соответствующее значение a=0,256, размеры поперечного сечения находим из Формулы (9.31). WК abb2= = 2.5 * 2.8, Откуда П2. 5а Двадцать пять 2>-0.256 см=3 > 38 см>h = 2>5Z’=2.5•3.38
см=8.45 см. Пример 32. Найти максимальное тангенциальное напряжение и угол кручения длины стального стержня 5 метров с поперечным сечением, как показано на рисунке. 216, авг. Стержень закручивается моментом, приложенным к его концам / VI K=5000 кгс * см. Для расчета напряжений и деформаций стержня при кручении необходимо разделить профиль на отдельные элементы. 216, б). Максимальное напряжение рассчитывается по формуле (9.28): ^ макс> К т / Макс Вычислите геометрические свойства, содержащиеся в последней формуле:=L<1+J k2+^KZ* Часть 1=45 мм;=35 мм;—=1,285; JKj= Л1 За столом. 14 в — =1,285 находим его,=0,221; pt=0,172. Тогда » 1 WKl==0,221 • 4,5 • 3,5 cm8=12. 2cm3; 224 для части 2 поперечного
сечения стержня h2=80 мм; B2=10 мм; аналогично находим Trk2=gM1— 0,307 • 8 • I2cm3=2. 5cm3; Jk2=P I M=°«3 0 7 • 8 • I3cm4=2. 5cm4; Джей К2 на WK2~1см- Девяносто пять =4,75. Для части 3 поперечного сечения стержня, h3=95 мм; B3-20 мм; — B3 20 Действуя как и прежде, G K3= «ZM z=0,288•9,5•2A cm3=10,9 cm3;4z=∫z M=0,288 • 9,5 • 2» см4=21,9 СМ4; 4×21. Девять » =W и m=2 и m — Так что 7K= = 41-B7K2 4 ′ 4z=53,2 -|- 2,5 -f-21, 9cm4=5/, 6cm4. Наибольшее отношение соответствует части 1 поперечного сечения, поэтому Наи-«к (Чем больше касательное напряжение Т находится в середине его длинной стороны. Находка-4. 57.6 С~<Л » 2.72 Т Макс==-/Т Г кгс / см2=236kgs/см», Угол закрутки стержня 5000 * 500 *=~G J T=8T W T5L6RDD = ° ’0 5 4 2R ad’
Смотрите также:
| Анализ напряженного состояния и разрушения при кручении | Кручение тонкостенных стержней |
| Расчет валов на прочность и жесткость при кручении | Расчет винтовых цилиндрических пружин |

