Оглавление:




Прямая задача в плоском напряженном состоянии. круг напряжений
- Прямая задача Он плоский, напряженный. Диапазон напряжения Аналитическое решение прямой задачи определяется по формуле(6.6)-(6.9). Проанализируем напряженное состояние с помощью простой графической структуры. Для этого рассмотрим геометрическую плоскость и отнесем ее к прямоугольным координатным осям o и T. порядок решений объясняется на примере состояния напряжений, показанного на рисунке. 159. Выбирая
определенную шкалу для напряжения, отложите абсциссу на оси(рис. 160) вырезать ОА=о; ов=О2. В AB, как и в диаметре, мы строим окружность с центром точки C. Построенный костыль называется кругом напряжения или кругом Мора. Координаты 167 точек окружности соответствуют нормальным и касательным напряжениям различных платформ. Таким образом, он удерживается под углом для определения напряжений участка(рис. 159),
из центра окружности с нарисуйте луч с углом 2A на пересечении Людмила Фирмаль
с окружностью точки Da (положительный угол откладывается против часовой стрелки). Абсцисса точки (отрезок _Oka) равна нормальному напряжению CGA, а ее ордината (отрезок KaDa) равна касательному напряжению TA. Радиус окружности п ОА-ОВ А. А.-О2 ~ ~ 2 ~ 2 Is-4 «ABOUT4» ^2, потому что центр окружности C лежит между точкой A и точкой B Два. 2. Тогда-R cos2A== Тогда точка » OK » =абсцисса OS+SC. 1 4-cos2A. 1-что-2А2. •И. / р<п\ =o, — — — — — — — — — — — — — — — — — — — — ~ Aa=R sin2A=~ — a-sin2A. (6.14)рассматривается напряжение на участке, угол пучка 2P=2 (A+j=*2A+l и, очевидно, вертикальная ось KpDp точки PR=-K»Da=-°2-sin2A=Tr (6.15), и, наконец, горизонтальная координата DPKR=O C-C из точки P = — K).-~ — ^ 4 ^ ——- cos2A=wk crf sin2a+<J2cos2a= = = op.
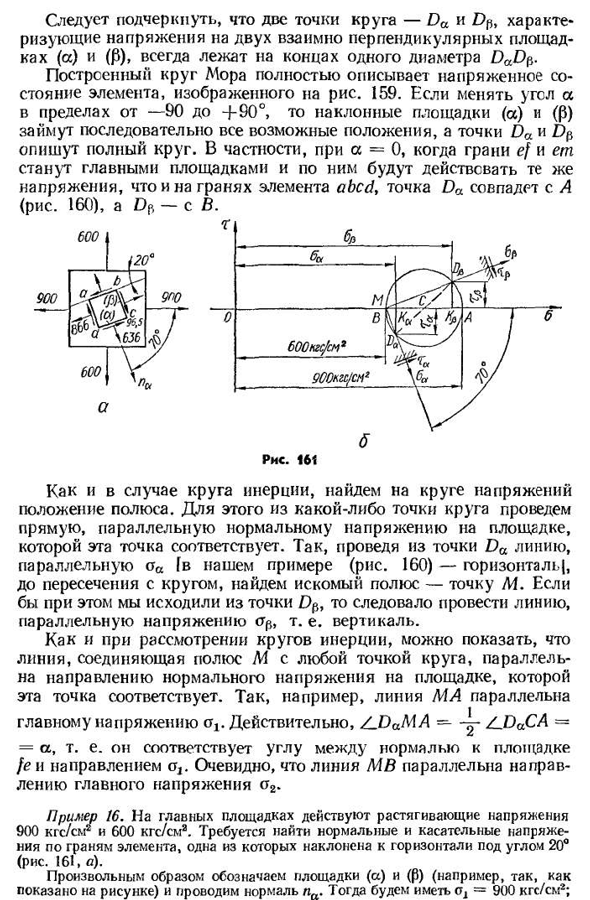
(6.16)формулы (6.13), (6.14)и формулы (6.6), (6.7)、 «Ка&а, та= , То, что мы хотели доказать. 168 следует подчеркнуть, что две точки окружности-Da и Dp, характеризующие напряжения на участке, перпендикулярном двум взаимно расположенным(а) и(0), всегда расположены в конце одного и того же диаметра Da Dp. Этот кротовый круг является полным представлением напряженного состояния элементов, показанных на рисунке. 159 изменяют угол а в диапазоне от −90°до+90°, наклонные платформы (а) и (0) занимают последовательно все возможные положения, точки Da и Dp
- представляют собой полный круг, в частности, в A=0, EF и et грани становятся основным участком, то же напряжение действует аналогично грани элемента abed, точки Da совпадают (рис. 160), в ДП-С. Рис сто шестьдесят один Найдите положение полюса на окружности напряжения, как в случае с инерционной окружностью. Для этого из любой точки окружности проведите линию, параллельную обычному напряжению на участке, где эта точка соответствует. Таким образом, нарисуйте линию, параллельную o из точки Da»[в этом примере (рис. 160) — по горизонтали, вплоть до пересечения с окружностью, находим искомую точку полюса M. Если исходить из точки Dp, то нужно провести линию, параллельную напряжению<Tr, т. е. Как и в случае
учета инерционного круга, указывается, что линия, соединяющая полюс м с любой точкой круга, параллельна направлению обычного напряжения соответствующего участка. Так, например, линия Ма фактически параллельна основному напряжению и соответствует углу между Zjama-Z_DaCA==a, то есть обычным K/si и STL. Ясно, что линия CF параллельна направлению главного напряжения P2. Пример 16. Напряжения растяжения 900KGE / cm2 и 600kgf / SMA работают на главном месте. Необходимо определить напряжения перпендикулярные и касательные к плоскости элемента, одно из которых горизонтально наклонено под углом 20°(рис. 161, а). Укажите место (а) и (0) (например, как показано на рисунке) произвольно и нарисуйте нормальное ПА.
После этого получаем результат (U2=900 кгс / см2; 169a3-600kgf / см2;<Г3-0;а=-70°. Поскольку Людмила Фирмаль
здесь он отсчитывается по часовой стрелке, угол a отрицателен. Решая эту прямую задачу, по уравнению (6.6) — (6.9)находим AA=ot cos2a+St2s’n2a= (900 • 0,117 4- 600 • 0,884) кгс / см2=636кгф / см2; dp — <h A2a4-A2cos2a= (900 • 0,884 4- 600 • 0,117) кгс / см2=866 кгс / см2;TA—Tr—1-ga sin2A — (-0,643)кгс / см2=-96,5 кгс / см2. Учитывая признаки расчетного напряжения, напряжение прикладывается к плоскости элемента abed(рис. 161, а). Граф может быть решен. 161, Б. после измерения получают координаты точек Da (3,18 см;-0,485 см) и (4,33 см;0,485 см). Принимая во внимание принятую шкалу(I см-200 кгс / см2), мы приходим к значению тех же напряжений, вычисленных выше. Кстати, одноосное напряженное состояние можно рассматривать как частный случай плоского состояния. В этом случае окружность напряжения проходит через начало координат (рис. 162). Наконец, для равномерного удлинения по всей окружности (<TX-SG2) и L и CJKa»TIA(O2-O3) молярная окружность изменяется на точки. Как уже упоминалось ранее, все сайты становятся основными.
Смотрите также:
| Линейное напряженное состояние | Обратная задача в плоском напряженном состоянии |
| Плоское напряженное состояние | Понятие об объемном напряженном состоянии |

