Оглавление:
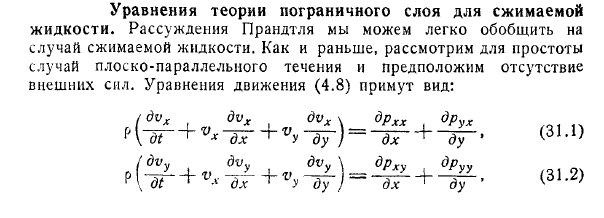




Уравнения теории пограничного слоя для сжимаемой жидкости
Уравнения теории пограничного слоя для сжимаемой
жидкости. Аргумент Прандтля может быть легко обобщен в случае сжимаемого fluids. As прежде для простоты рассмотрим случай плоскопараллельных течений и предположим, что внешних сил нет.
Смотрите также:
- Методические указания по гидромеханике
- Интегральное соотношение Кармана и его обобщения.
- Пограничный слой в несжимаемой жидкости вдоль плоской пластинки.
На то обстоятельство, что прилипание жидкости может оказать существенное влияние на характер течения и его закономерности, указано ещё в гидродинамике Д. Бернулли. Людмила Фирмаль
- Уравнение движения (4. 8) принимает вид: _ _ oruh dpx с ду) ДХ ду * duu _ _ drhu {друу ду / ДХ ду ’ Руу = — Р + <х + Ту- + Х Х Уравнение неразрывности выглядит следующим образом: л д (’ДХ’ ду ДХ ДУ в ДУ / * интегрируйте y от 0 до 5: ДХ г у / г » пойти
Но из уравнения неразрывности Укажите как и раньше год>*〜 Вставка (о>). Если перейти от (31. 12) к (31. 11) и взять производную из-под знака интеграла и уменьшить ее, то: (31. 13 Это интегральное отношение Калмана сжимаемых жидкостей. а = СР $ 1. Если / x = cp $ 1. Перейти автоматически (30. 13).

