Оглавление:




Построение эпюр внутренних усилий для пространственных стержней
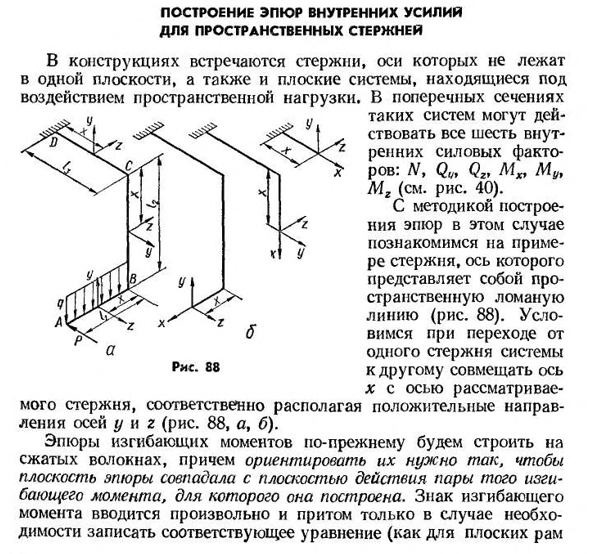
- Внутренняя силовая схема Для пространственной палки В конструкции имеются стержни, оси которых находятся не в одной плоскости, а плоские системы под воздействием пространственных нагрузок. В поперечном сечении таких систем могут действовать все шесть внутренних силовых факторов:/V, Qf/, Qz, M x, Mu, M g(см. 40). Методом построения графика в данном случае является пример
стержня (рис. 88). Согласуют переход от одного стержня к другому в системе, совмещающей оси стержней, рассматриваемых по оси x и имеющих положительные направления оси y и оси g соответственно (88, a, b). График изгибающего момента по-прежнему строится на сжатом волокне, а плоскость графика вводится произвольно только тогда, когда знак изгибающего момента должен записать соответствующее уравнение (в случае плоской рамы),
чтобы оно совпадало с рабочей плоскостью пары изгибающих моментов, Людмила Фирмаль
подлежащих построению 78i криволинейные стержни). В случае продольных сил и крутящих моментов соблюдаются те же правила кодекса. Графики N и L4ir можно ориентировать как угодно, но вертикальная ось всегда будет перпендикулярна оси стержня. Боковые силы в поперечном сечении считаются положительными, если их направление совпадает с положительным направлением осей y и g. Строительство начинается на площадке АВ. Для любого
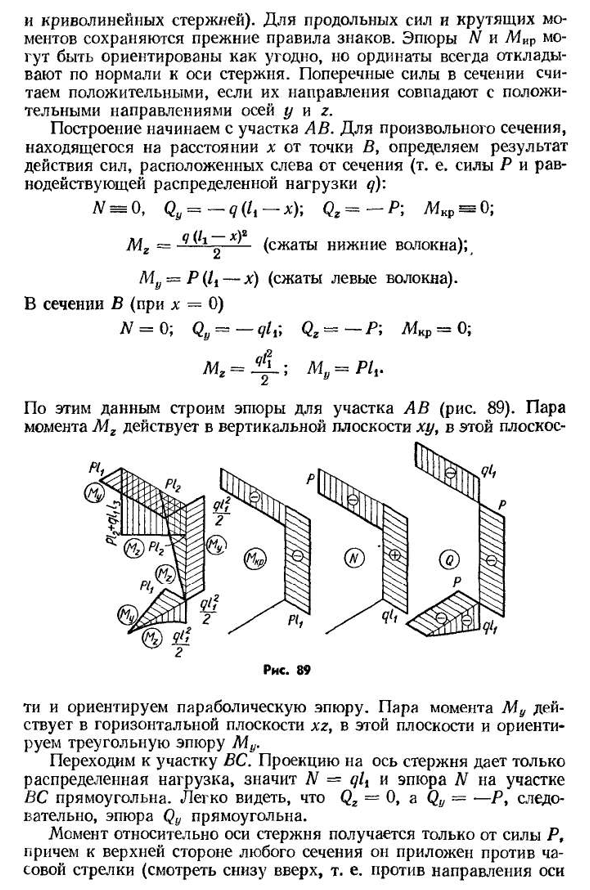
участка, расположенного на расстоянии x от точки B, определите результат действия силы, расположенной слева от участка (т. е. силу P и результирующую нагрузку q). Сечение B (x=0) N=0; Qy~ — ql ti Qz~ — Pi NIKp-0; фольксваген Два. =4~;иы = р он. По этим данным строят график сечений AB (рис. 89). Пара моментов, M g, действует на вертикальной плоскости, XY, в этой плоскости- Райс, восемьдесят
- девять поворот ti и участок параболы. В этой плоскости мы ориентируем график Mu треугольника. Переход к участку солнца. Так как проекция на ось стержня дает только распределительную нагрузку, то участки N=ql±и VS сечения участков N имеют прямоугольную форму. Легко видеть, что Q2=0, Qy= — P и, следовательно, график Qy является прямоугольником. Момент для оси стержня получается только из Силы Р и прикладывается против часовой стрелки на верхней стороне любого сечения (снизу вверх, то есть в направлении оси). 79х). Согласно принятым правилам знаков для крутящего момента секции самолета М КР — — Участок
MD прямоугольный Изгибающий момент фигур BC сечений MD и Mg представляет собой прямые линии, так как на них нет распределенной нагрузки. Следовательно, поскольку и сила P, и результат распределенной нагрузки проходят через ось z этого участка, момент MG-o участка не имеет отношения к двум участкам, B и C. Мг=П / 2. Момент распределения нагрузки Mg результата не дает в этом сечении, но пересекает ось z сечения C, поэтому согласно этим данным треугольник mg (рис. 89)на сжатом волокне размещается в плоскости, в которой действует изгибающий момент MG пары. Для му гнуть времена в разделах Б и к Сила P параллельна этим осям, поэтому она не дает момента осям y в сечениях B и C.
Таким образом, участок M v на графике VS является прямоугольным. Для риса. Этот прямоугольник построен на сжатом волокне и помещен Людмила Фирмаль
в плоскость xz. Диаграмма участка, построенная на компакт-диске. Только сила P проецируется на ось x, что приводит к сжатию. Так что здесь W= — P И участок продольной силы прямоугольный. В любом сечении участка Qz=0, Qy=-qlit следовательно, участок Qy прямоугольный. Момент для оси X получается только из действия q (P параллельно оси x), и по допустимым правилам знака крутящего момента этот момент отрицателен: Я КЖ и Участок№ 1№снова получается прямоугольником. Поскольку фигуры изгибающих моментов M y и M g являются прямыми линиями, вычислите
их значения только в двух сечениях C и D: Mg=P*BC=R1g (сжатый).); Раздел 80Б мг Д-р■до н. э.+ * компакт-Р12(сжатые волокна снизу); му-Р * АБ-ПЛТ(слева сжатого волокна). На основании этих данных был построен трапециевидный график изгибающего момента Μ в горизонтальной плоскости и изгибающего момента M g в вертикальной плоскости. С помощью этих графиков можно найти значение и направление любого сечения пространственного стержня (89) При изгибе и кручении возникают продольные и поперечные
силы. Сила и момент сечения D показаны на рисунке(Рис. 90). Вот вам пример. Создадим график пространственно нагруженного криволинейного стержня(рис. 91, а), расположенных в горизонтальной плоскости. Его сечение (например, показанное на схеме прямоугольной пунктирной линией) таково, что одна из главных центральных осей совпадает с направлением радиуса, обращенного к центру тяжести (ц). Сечение, а второе-z-вертикальное. Касательная окружности указывает направление оси стержня (оси x) каждого сечения. Сила Р вертикальна, внешний момент м приложен
к плоскости концевой части А. Таблица 9 Один. f°0 15 30 | 45 60 75 90 2 sin f0 0.259 0.500 0.707 0.866 0.966 1 3COS f1 0,966 0,866 0,707 0,500 0,259 0 4 8000 (3] 8000 7730 6930 5660 4000 2070 0 5L1cr= [4| — 6000 2000 1730 930 −340 −2000 −3930 −6000 6 M=8000421 0 2070 4000 5660 6930 7730 8000 В этом случае для построения графика необходимо ввести угловые координаты f и написать формулу силы и момента. В этом случае легче рассмотреть проекцию стержня на горизонтальную плоскость(рис. 91, б). Ось g совпадает с точкой C, обозначенной точками в окружности, сила P обозначена крестом между точкой A и окружностью, а приложенный внешний момент представлен в виде векторного момента. Рассмотрев результат действия силы,
приложенной к стержню в текущем сечении C, вычислите путем умножения плеча, соответствующего P изгибающему моменту, на силу P$1P<reel£=DC = P(1-cos f). Мысленно перенесем вектор M A В точку C для вычисления компонент M и MKR от действия момента MA(рис. 91, 6). Проекция этого вектора на ось Y и ось x дает компоненты изгиба и крутящего момента соответственно Придерживаясь принятых правил маркировки для L4cr и вызывая сжатие в нижних прядях стержня, считая M положительным, получаем следующее: L1 (L1! — Собф)+Ма Кос Ф-(П7? + / IL) Собф-Р/?.
Р=200kgf, Ма-2000kgf-см,£ = 30СМ м(ф)=ф 8000sin кгс * см; L1K п (ф)=(ф 8000cos-6000) кгс * см. Составьте таблицу(табл. 9) и на полученных данных строим график M и L1kr(рис. 92). Иногда сюжет пространственно нагруженного криволинейного стержня строится не на проекции стержня, как это сделано на рисунке. 92, а в перспективе(рис. 93).
Смотрите также:

