Оглавление:




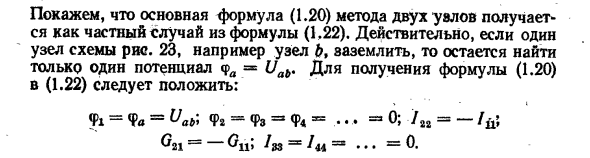

Метод узловых потенциалов
Метод узловых потенциалов. Ток в ветви цепи можно найти по закону Ома участка цепи, содержащего э. d. to применяя закон s-Ома, нужно знать потенциал узлов схемы. Метод расчета электрической цепи называется методом узлового потенциала, рассматривая потенциал узлов цепи как неизвестные величины.
- Предположим, что в схеме имеется n узлов. Любая (1) точка цепи, распределение тока и I *• Я имею право мысленно заземлить 1 из узлов схемы. Число неизвестных уменьшается от n (n-1).
То есть, вы имеете право принять потенциал равным нулю. Людмила Фирмаль
Число неизвестных в узловом потенциальном законе равно числу уравнений, которые должны быть составлены для схемы по первому закону Кирхгофа. Метод потенциала узла, такой как метод тока петли, является одним из основных методов расчета. Если число узлов без блока меньше числа независимых петель в цепи, то этот метод более экономичен, чем метод тока петли. ‘•
Переходим к фигуре из фигуры в фигуру. 24.Схема имеет достаточно большое количество ветвей (11 ветвей) и относительно небольшое количество узлов(4 uapa).Если один из узлов схемы, например, узел 4, мысленно заземлен, то есть r)] i; / — i£; 2-(F1-fl 1 g’N + + [^ 21(Ф1Фа)] «и» B 1^.1 (Ф1Фх) 1 ″ и〜
- Перепишем последнее уравнение следующим образом: — ■φ/ * μφ^ ^ 12 «bФз ^ 13» ^ ц — (1.21) Здесь. С11 =£4!+£13 + ^ 2 + ^ 1 +#12 +£12″» ’ГИА=-(£12 + +£’ 2); °1 второй=〜 Л1 =£14 + £ 31С! + ^ 21£21〜^ 4 ^ 41 ^ 12£2Г Описывает структуру выражения (1.21). ₽ ₽ Сюда входит коэффициент GN, который равен сумме проводимости всех ветвей, сходящихся на первом узле, и 612 равен сумме проводимости всех ветвей, соединяющих узел 1 с узлом 2 со знаком минус.
Аналогично, 613-это сумма проводимости всех ветвей, соединяющих узел/с узлом 5, со знаком минус. Current / n называется узловым током первого узла.
Это вычисленное значение, равное алгебраической сумме токов, полученных путем деления e. d. ветви, соответствующей s-узлу / сопротивлению этих ветвей. Людмила Фирмаль
Эта сумма со знаком плюс включает в себя ток этих ветвей. D. S. обратите внимание, что проводимость, записанная в приведенных выше 2 индексах, не имеет никакого отношения к входной и взаимной проводимости ветвей, рассмотренных в§ 14. Вы можете написать аналогичную формулу для остальных узлов схемы.
Если схема имеет n узлов, то она соответствует системе уравнений (n-1) вида: ΦD1+Д2^и+•••+»» 1 ^ | 1 = /ц*、 ФAi +Фз ^ еа + * * * • фл-1 ^ 2, п-1-i22 ’» (1.22) ΦD-1.14 Фг ^ L-1, 2 +•••+ Фп-lqn-1. n-1 ^ n-1, n-1 Где Gkk-сумма проводимости ветвей, сходящихся в узле k\ Gkm-сумма проводимости ветвей, соединяющих узел k и m знаком минус. lkk-это текущий k-узел узла. Если ток течет от источника тока к k-узлу, текущий Ikk должен содержать знак плюс и знак минус, если есть утечка.
Если нет ветви между 2 узлами, соответствующая проводимость равна нулю. После решения системы (1.22) относительно потенциала ток определяется в ответвлении по закону Ома в участке цепи, содержащем Э. Д. С.
Пример 13.Найдите ток в ответвлении цепи на рисунке. 24 n выполните проверку в соответствии со вторым законом Кирхгофа. Дано:£’, = 10 В, E \ 4 = 6 В, E \ 2 = 20 в,£2 | = 30 в, E31 = 14 в, Eu-10 в,£43 = 8 в,£23 = ^ zr = 7r «= 1 ом’ = ?? 2 = 10 ом, да?? 2 = 10 ом, верно?? ’, ’= 5 ol.? 31 = 2 авг.24 = 4ol<.? 34 = 2 ом, R ’ ^ = 4 ом, p ^ = 2 ом.
Источник тока, подключенный между узлами 3 и 2, дает ток/ L32 = 1,5 А. Решение: запишите систему уравнений ДД1Ч-Ф2^ 12 +Фз^Лз= ^ц>Ф1^ 21 4 «Фг^ 22 4″Фе^ 23 = И22″Ф1^ 31 4〜Фг^з24〜Фз^зз〜Лз* Отсчет проводимости = 0.2 + 0.1 + 0.1 + 0.25 + 0.25 + 0.5 = 1.4(сим)’、 ГМ= = 0.5 + 0.5 + 0.25 + 0.5 = 1.75(сим)-、 *> 23 ^ 23 ″ 31#34 Г «= Г» =-(0.2 + 0.1 +0.1)= −0.4 (СИМ G3j = Г13 = сим 0.5 ’、 G ^ = G32—(0.25 4-0.5)=-0.75(диплом).
При расчете G22, G33 и GM учитывалось, что проводимость ветви с источником тока равна нулю (сопротивление источника тока бесконечно). Тенденция энергосбережения F32 из ф23 ■ фут2 ^ 21 åa<Л, 1 ПЗ р * * р р * р ’ * ^ 32 a32 * ’ 23 +2 * ^ 21 A24 Один / 33 =-3.5 4-3-7-4-4-1.5 =-5(а).
Одновременные уравнения 2.4 ФГ-Ф2 0.4-0.5 <па = 15; ’-0.4 ph14-1.4 <Р2-0.75 пгц = −1.5; −0.5 Q> я-0.75 <па + 1. 75f3—5. Системный идентификатор < Пи= 2.4 −0.4 −0.5 А = −0.4 1.4 −0.75 0.5-0.75-1.75 / 15 −0.4 −0.5 1-1. 5 1.4 −0.75 Я −5 −0.75 1.75 Один 2.4 15 −0.5 −0.4 −1.5 −0.75 −0.5 −5 1.75 Один = 3,62. = М = 6(е). 3.62 1 7 4, «= я ^ = −1 ′ 107(е)-
Заключительным этапом расчета является расчет тока по закону Ома. Конечно, прежде чем определить ток ветви цепи, необходимо определить эти токи и выбрать для них положительное направление.
Напомним, что согласно принятой в этом пункте нотации, первый индекс тока дает номер узла 1, а второй индекс дает количество узлов, через которые протекает ток. ; _ ^ — (Х1-Х4)_ 10 — (6-0) = 4 (а); ’*41 И я (Ф1-ФА) (б-0.06) J21» — =. — ==-1.185 (а); < 2 b 5 4 ’ Д _ ^ 32-(Ф1-ч>>)7-(0,06 + 1,1)5.84 −2.92 (а); 32 -= — =〜 /» = = 8-(-1.107-0)-4.55(о) и др. ₽ ₽ 432
Рассмотрим решение по закону 2-го Кирхгофа периферийных цепей. * Алгебраическая сумма падения напряжения 4.1-(-1.185)).5-2.92.2-4.55.2 «-5(в). Алгебраическая сумма e. d. S равна 10-7 −8 = −5 (е).
Основная формула для 2-узлового метода (1.20) указывает на то, что он получен как частный случай из Формулы (1.22).фактически, 1 узел схемы на рисунке 1 остается найти только 23, например, узел b заземлен и 1 потенциал<pa = Uab. Чтобы получить выражение (1.22) (1.20), необходимо ввести: Ф1» Фа = Century»ФЗ » Ф4 век.•••* = = м Ар = ч» G21 = Gn; / 33 = / 44 = … = 0.
Смотрите также:

