Оглавление:




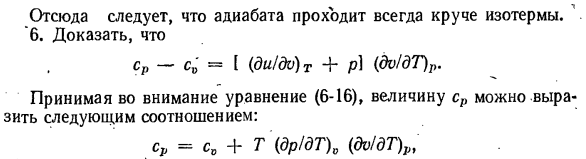

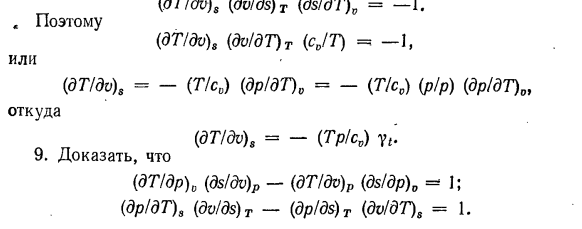

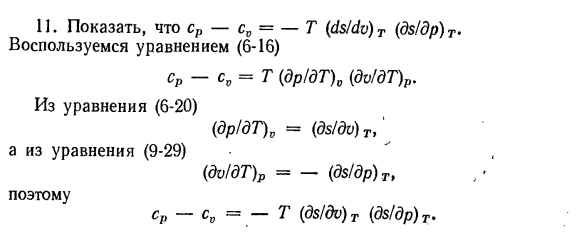


Приложение дифференциальных уравнений к решению некоторых термодинамических задач
- Применение дифференциальных уравнений к решению некоторых термодинамических задач 1.Идеальные газы Cp и Su не зависят от давления и объема при T-const. Из Формулы (10-22)、 (УДС / др) т = — т(d2V / ДТ . и если мы используем p-const для дифференцирования уравнения состояния、 (dVldT) в = г / с. Вторая производная от частной производной (d2V / dT2) p = 0、 И так оно и есть.、 (ЦОС / Д П)М = 0. Теплоемкость идеального газа при постоянной температуре
не зависит от давления. Из Формулы (10-23)、 (dCv / dV) T = T (d2p / dT2) y. если вы дифференцируете уравнение состояния с V-const, оно выглядит так: (доктор! dT) y = mR / V вторая производная этой производной является (d2p / dT \ = 0、 И так оно и есть.、 — (врпэ / DV) Т-0 Изотоническая теплоемкость идеального газа Cv зависит от объема и, следовательно, от давления. 2 внутренняя энергия идеального газа зависит только от температуры,
Согласно закону Джоуля Людмила Фирмаль
а не на объем и давление. В настоящих Правилах、 (dU / dV) T = 0 и (dU / dp) T = 0 что получается из уравнения состояния: (ДП / ДТ) V в = г / в; (ДВ / ДТ) Р = мр / р; (дв / ДП) Т = —МРТ / п \ Значение по формуле (10-7) (dp! Если вы назначаете (dU / dV) T =Γ(φ/ >>-p-T(mR / V) — / 7 = 0. (дв / ДТ) р и (ДК / д/?Если вы присваиваете значение G формуле (10-10)、 。 (dU / dp) T = — [Г (dWdT) p + p (dV / dp) т] = «•=-[ГМ// 7) — / 7 (MRT / p*) \ = 0.Идеальный случай для газа」 (dUldT)в = ДУ / ДТ = ТИЦ. 3.Внутренняя энергия газа определяется по формуле ван-дер-Ваальса.
Из уравнения ван-дер-Ваальса p = n7y(a_b)-(a / v2) и(dr / dT) 0 = 7?подставляя значение производной /(v-b) в Формулу (10-12), получаем следующую формулу:•dU = IT (dr / dT) 0 p] dv + c0dT И = I TR /(v-6) 1 dv-PDV + DT подставляя значение p в полученное уравнение, получаем: ДТФ = л(ТР /(в-6)1 ДУ-ЛРТ /(в-6) 1 ДУ — (А / В2) ДВ + + c0dt cvdT — (А / В9) делать. 4. На Ts-диаграмме докажите, что изолинии выпуклы в направлении оси абсцисс. Чтобы доказать это, квадратичная производная (d277ds2) г>0.из Формулы V-const (6-46)、 du0 = TdsD.
- Учитывая формулу (6-5)、 =(dU / dT) 0 = T (dsIdT) 99 Отсюда 。 (dT / ds) если 0 = T / s0 t ^-c0 = const, то используйте производную 2-го порядка. У2 Жо ДС ли ДС) в J0-ДС у Джо ЧВ [ДС) 0 в D ’ Теплопроводность при постоянном объеме cD> 0 и Г> 0, а следовательно d * r / ds%> 0 В результате на диаграмме Ts равнобедренные точки выпуклы по направлению к абсциссе. 5.Используя дифференциальные уравнения Изотерм в частных производных и коэффициенты адиабатического сжатия, мы доказываем, что адиабата проходит круто над изотермами. dQ = 0 и ds = 0, разделив уравнение (10-14)
на (10-13)、 СР (др / ДТ) о (ДР \ ЧВ (кб3!ДТ) П〜 \ ДВ)$’ Подставляя значение формулы (4-8) (dr / dT) 0, получаем: / ДП \ СР (др / ду) Т.(до / ДГ) Р ЧВ(ДВ / ДТ) Р Откуда же. ^»<адрес>». (Св / ДВ) = а к (ДП! ДВ) т. Коэффициент адиабатического сжатия p8 является k-кратным коэффициентом изотермического сжатия pg:•% ПС = кпт. В результате изоляция всегда будет круче, чем изотермы. 6 СР-С0 = [(ду / DV) т + п) (ДВ / ДТ) р. Принимая во внимание уравнение(6-16), значения cp выражаются в следующих
.Доказать это Людмила Фирмаль
соотношениях: СР = СV + Т (др / ДТ) 0 (ДВ / ДТ) ст И из Формулы(10-7)、 Т (Ди / ДТ + р » & р / ДТ) 0 Подставляя значение T в предыдущее уравнение, получаем: с > = С°+ [<ДР / ДТ ш ^ щ (ФП / пп) в Откуда = СV + + п (<^/ДГ) Р Или — cv f. l (du / dv) T + p] (dv / dT) pt Где термин p (di / dT) P представляет внешнюю работу, полученную при изменении температуры на Г, а термин(du / dv) T (dv / dT) p дает изменение внутренней энергии при повышении температуры Г при постоянном
давлении. 7.С формулами (6-46) и (10-13)、 (ДТ / ДВ) у =(п-т (ДП / ДТ) 0Vcv. Если сравнить формулы (6-46) и (10-13), то получим: du = Tds-pdv] ds =(cydT)/ T +(dr / dT)0 dv \ du = cvdT + T ( И так оно и есть.、 СР-С0 =-Т (ДС / ДВ) Т(ДС / ДП) Т 12.Определить термодинамические функции независимых переменных p, f и T, F. получить уравнение (6-47) ТДС = дл-ВДП. Для независимых переменных p и f термодинамической функцией является энтропия 5 (p, f). dS = dl / T — (K / T) cfp. At постоянное давление И затем (ДС / ДП)、 В ^ — ИД / дБ (ди (ДС)= п (ДС / ДП) П■ Напишите формулу(9-15). ДФ — СДТ-ДПК. Для независимых переменных T и F термодинамическая функция равна объему V (7 \ F). dV = — d / 7p — (S / p) dT при постоянной температуре (дв / ДТ) Р
Из уравнения ван-дер-Ваальса p = n7y(a_b)-(a / v2) и(dr / dT) 0 = 7?подставляя значение производной /(v-b) в Формулу (10-12), получаем следующую формулу:•dU = IT (dr / dT) 0 p] dv + c0dT И = I TR /(v-6) 1 dv-PDV + DT подставляя значение p в полученное уравнение, получаем: ДТФ = л(ТР /(в-6)1 ДУ-ЛРТ /(в-6) 1 ДУ — (А / В2) ДВ + + c0dt cvdT — (А / В9) делать. 4. На Ts-диаграмме докажите, что изолинии выпуклы в направлении оси абсцисс. Чтобы доказать это, квадратичная производная (d277ds2) г>0.из Формулы V-const (6-46)、 du0 = TdsD.
Учитывая формулу (6-5)、 =(dU / dT) 0 = T (dsIdT) 99 Отсюда 。 (dT / ds) если 0 = T / s0 t ^-c0 = const, то используйте производную 2-го порядка. У2 Жо ДС ли ДС) в J0-ДС у Джо ЧВ [ДС) 0 в D ’ Теплопроводность при постоянном объеме cD> 0 и Г> 0, а следовательно d * r / ds%> 0 В результате на диаграмме Ts равнобедренные точки выпуклы по направлению к абсциссе. 5.Используя дифференциальные уравнения Изотерм в частных производных и коэффициенты адиабатического сжатия, мы доказываем, что адиабата проходит круто над изотермами. dQ = 0 и ds = 0, разделив уравнение (10-14) на (10-13)、 СР (др / ДТ) о (ДР \ ЧВ (кб3!ДТ) П〜 \ ДВ)$’ Подставляя значение формулы (4-8) (dr / dT) 0, получаем: / ДП \ СР (др / ду) Т.(до / ДГ)
Р ЧВ(ДВ / ДТ) Р Откуда же. ^»<адрес>». (Св / ДВ) = а к (ДП! ДВ) т. Коэффициент адиабатического сжатия p8 является k-кратным коэффициентом изотермического сжатия pg:•% ПС = кпт. В результате изоляция всегда будет круче, чем изотермы. 6.Доказать это СР-С0 = [(ду / DV) т + п) (ДВ / ДТ) р. Принимая во внимание уравнение(6-16), значения cp выражаются в следующих соотношениях: СР = СV + Т (др / ДТ) 0 (ДВ / ДТ) ст И из Формулы(10-7)、
Т (Ди / ДТ + р » & р / ДТ) 0 Подставляя значение T в предыдущее уравнение, получаем: с > = С°+ [<ДР / ДТ ш ^ щ (ФП / пп) в Откуда = СV + + п (<^/ДГ) Р Или — cv f. l (du / dv) T + p] (dv / dT) pt Где термин p (di / dT) P представляет внешнюю работу, полученную при изменении температуры на Г, а термин(du / dv) T (dv / dT) p дает изменение внутренней энергии при повышении температуры Г при постоянном
давлении. 7.С формулами (6-46) и (10-13)、 (ДТ / ДВ) у =(п-т (ДП / ДТ) 0Vcv. Если сравнить формулы (6-46) и (10-13), то получим: du = Tds-pdv] ds =(cydT)/ T +(dr / dT)0 dv \ du = cvdT + T ( И так оно и есть.、 СР-С0 =-Т (ДС / ДВ) Т(ДС / ДП) Т 12.Определить термодинамические функции независимых переменных p, f и T, F. получить уравнение (6-47) ТДС = дл-ВДП. Для независимых переменных p и f термодинамической
функцией является энтропия 5 (p, f). dS = dl / T — (K / T) cfp. At постоянное давление И затем (ДС / ДП)、 В ^ — ИД / дБ (ди (ДС)= п (ДС / ДП) П■ Напишите формулу(9-15). ДФ — СДТ-ДПК. Для независимых переменных T и F термодинамическая функция равна объему V (7 \ F). dV = — d / 7p — (S / p) dT при постоянной температуре (дв / ДТ) Р
Смотрите также:
Решение задач по термодинамике
| Уравнение Клапейрона — Клаузиуса | Основные понятия и определения водяного пара |
| Тепловая теорема Нернста | Особенности диаграммы водяного пара |

