Оглавление:



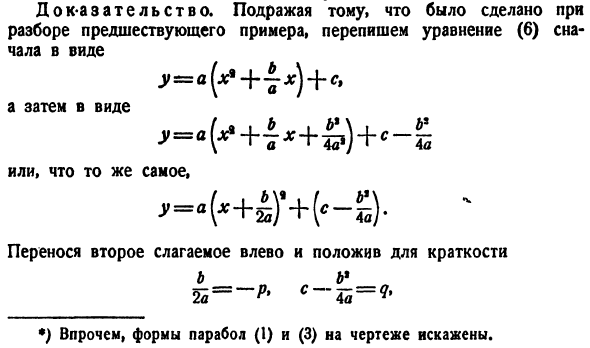











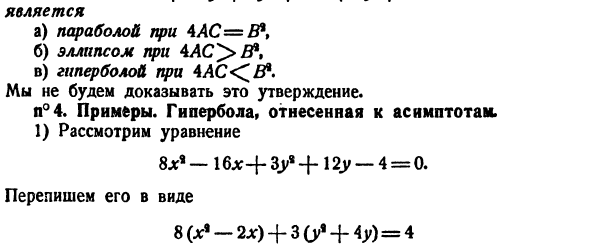






Упрощение уравнений кривых 2-го порядка
- Упрощение уравнения кривой 2-го порядка Н°1.Уравнение y = axh — \ — bx — {- c. в этом разделе описывается применение преобразований координат для упрощения уравнения 2-й строки. Давайте начнем с примера. Предположим, вы хотите найти линию, которая соответствует уравнению. у = 12л:+ 9.(!) объедините члены,
содержащие x, и перепишите это уравнение. вы добавите выражение в скобках с полным квадратом, вы получите: у = 3(х *-4х + 4)+ 9-12 Или то же самое у + 3 = 3(ок-2)’. (2) Это исходное уравнение (1), но только если группа членов отличается. Предположим, что здесь система координат переведена и начало
у = 3(х *-4х) −9. Если Людмила Фирмаль
координат перемещено в точку 0 (p, q).Тогда старые координаты всех точек плоскости (x, y) представляются новыми координатами(xlt бьется по формуле). х = ХВ + р, г = г \ + <1- Итак, в новых координатах уравнение прямой принимает вид: У1 + д + р = Тх1 + п-2)\(3) Вы можете выбрать точку Oi. Впустить меня. П =%Д =-3. При таком выборе p и q выражение(3) не является просто очень простой
формой*) Ух = 3*}. (4 )) Но что еще более важно, оказывается, что это форма уже известного нам параболического уравнения. Уравнения(1) и (4) являются уравнениями одной прямой, поэтому уравнение(1)является параболическим уравнением. Эта парабола имеет вершину в точке Oj (2, −3) и симметрична. ( * ) Это именно идея выбора P-и q-значений, и читатель может легко увидеть, что для другого q вы получаете более сложную формулу, чем(4). Он находится на оси 0 \ X \относительно линии O ^ yi. It удобно сравнивать эту
- параболу с параболой у = 3х \(5) Форма и размер этой новой параболы полностью идентичны параболе (4), но ясно, что только вершина находится не в новой параболе, а в старом начале координат, и ее ось симметрии не новая, а в старой вертикали coordinate. In другими словами, парабола (4) является результатом такого перевода параболы (5), на вершине которой она движется
к точке Ot (2, −3).Но, как уже говорилось, парабола(4) — это всего лишь парабола (1) (читатели должны четко понимать, что (1) и (4) — это одни и те же линейные уравнения, но только в разных системах координат)!это так not. So уравнение(1) является уравнением параболы, полученным из параболы(5). Используйте параллельную передачу. Все вышеперечисленное показано на рисунке*). 76. рассмотрев пример стота, уже легко понять следующую теорему:
Уравнение (б) у = ах * — J в-ВХ м \ м С9 Здесь afO Людмила Фирмаль
Теорема. соответствует параболе, полученной из параболы у = АХ *(7) Используйте параллельную передачу. Y、\ ыы З 4 * -/ −2 __ N л Дж < 7 О 76. Доказательство. Сначала перепишите выражение (6) в следующем виде, имитируя то, что было сделано при анализе предыдущего примера. Причем в форме Или то же самое Переместите 2-й член
влево, чтобы сделать его кратким Б Б1 ( * ) Однако формы парабол (I) и (3) на рисунке искажены. Наконец, дайте форму выражения(6 г-д = а (хр)\(8) Теперь сделайте параллельный перенос системы координат и переместите начало координат в Oj (p, q\), вам нужно поместить x = xx — {- p, y = yl — {- Q. Это назначение преобразует уравнение(8) в уравнение Ух = * А-(9) Таким образом, формула(6) является(в старой
системе координат!)) Соответствует линии, соответствующей формуле (9) в новой системе координат. И этот последний ряд имеет ту же форму и размер, что и парабола(7). Для того чтобы соединить параболу (7) и параболу (6), нужно просто перевести первую в перевод, а на ее вершине перейти к точке Oi (pt q).Теорема доказана. Примечания, 1) Форма параболы y = ax%полностью определяется значением коэффициента A. поскольку парабола y = ax * — * bx — \ —
c имеет одинаковую форму из 3 коэффициентов a, b и c, только коэффициент a влияет на форму параболы y = ax * — \ — bx — \ — c. коэффициенты b и c(и a!) Влияет только на положение вершины параболы. 2) по аналогии с теоремой 1 устанавливаются следующие уравнения: х = АУ *- \ — с — \ — с(9 * 0) Ось симметрии соответствует параболе, параллельной оси Ox. н°2.Уравнение ччч — \ — cy% — \ — DX —
\ — EY — \ — F = Q нашей основной задачей является изучение наиболее распространенных уравнений 2-го порядка Ax * + Bxy + Cy * + Dx — {- Ey — {- F = 0. (10 )) Задача значительно упрощается в частном случае B = 0, то есть когда произведение координаты xy не входит в формулу(10). Теорема 2.Уравнение О, да. Ах *- \ — ТИЦ * + ДХ + ЕУ + Ф = 0 Она соответствует любой кривой, будь то эллипс, парабола или
гипербола. Прежде чем доказывать теорему, объясните, почему утверждение начинается с условного поворота. Дело в том, что иногда формула (11) вообще не совпадает на плоскости. Нет никаких геометрических образов. Таково, например, уравнение B * с + 7y1 = −8. (12) Иногда уравнение(11) соответствует точке, а не линии. Это потому, что уравнение является 5 * » + 7ua = 0, (13) Соответствует началу координат. Однако в указанных случаях возможные задачи
не решаются * действительно, в обычном смысле слова » кривая*«, определенная кривая, например, уравнение 9jc4-4y * = 0(14) Не кривая, а пара линий: Поскольку 3x-2y = 0,3 x + 2y = 0, уравнение(14) можно переписать в виде (3 х-2У) (3х-2У)= 0、 И понятно, что свести к нулю письменную работу можно только на 1 factors. It это как уравнение. x * = 0 (15) Уравнение,
соответствующее строке * = 0 −3 * 4-2 = 0(16) Пары линий x = 1 и x = 2.Я хотел бы исключить такой случай из условной формы, в которой сформулирована теорема. Отсюда и термин. Кривая*означает кривую. Переходя к доказательству, мы сначала предполагаем, что либо коэффициент A, либо C равен zero. In в этом случае формула (11) становится уравнением 1-го порядка, и эти коэффициенты нельзя стирать одновременно, так как прямая линия соответствует it.
To будьте ясны С = 0, АФ 0.- Вид уравнения (11) имеет вид Ах * — {- ДХ + ЕУ + Ф = 0、 Это тот тип уравнения, который мы рассмотрели выше. у = ах *-\-ьх-\ — с(aφ0)、 И мы уже знаем, что она соответствует параболе. Аналогично, при A = 0, CΦ0 парабола соответствует уравнению (11), только ее ось симметрии становится параллельной оси Ox, а не оси Oy, как если бы она принималась во внимание. Теперь
вернитесь к Af 0 и Cf 0.In в этом случае выражение (11) можно переписать в следующем виде: Или, короче говоря、 А(Х-р)* + с(г-Кудс = * М9 Если применимо**) Д Е Лл Д9, е Р = — 2А ’ 1 = 4А * 4С Если мы сделаем перевод системы координат и переместим начало координат в точку 0 \(p, q), то в новой системе кривая (II) получит уравнение х \ + Су \ = М (17) И его можно переписать в виде*) 2. различают две возможности.1) коэффициенты A и C имеют один
и тот же знак, и 2)они имеют разные знаки. Давайте сначала поговорим о первом случае. Для ясности пусть Λ> 0 и C> 0 ( * ).И понятно, что это Λ1> 0.In дело в том, что если M = 0, то выражение (17) не является кривой, а соответствует точке, как в Примере (13), а неравенство 0 приводит к тому, что нет ничего, что соответствует выражению (17), например (12).Поэтому остается только возможность M> 0. Перепишите выражение (17) в следующий
формат •) Понятно, что это Еф 0.В противном случае выражение(11) будет иметь вид Ax * — * — Dx — * + ^ = 0 и будет соответствовать паре строк[подобно выражению(16)]. Рычание (15)]вообще никакого ответа «9 мая внимательно следите за процессом умозаключения. Но учтите, что вы не хотите запоминать выражение ru q, At. Do не загружайте ненужные детали в память. •* * ) В противном случае измените знак
на обеих сторонах уравнения(17). Ич I_1 „LG +“ LG-1 Или,=(это、 Дроби положительные), в виде] ФЛ-П-21-1 * б% Это эллиптическое уравнение. Необходимо учитывать, когда А и С — это количество различных знаков. В противном случае, поскольку он изменяет знак с обеих сторон выражения (17), мы можем предположить, что O, C <0.As упомянутый выше,
легко проверить MFI. In дело в том, что если A> 0, C <0, M = 0, то уравнение(17) является не кривой, а парой прямых линий, как мы видели в примере (14).Отсюда и Mf0.Для ясности предположим, что это Λ1> 0.Переписывание формулы (18) из Формулы (17) если вы поставите — = ^ = — b, он достигнет уравнения. О1-б * ’ То есть к гиперболическому уравнению. Теорема доказана. Замечание. 1) метод доказательства теоремы, примененный к определенному уравнению, фактически делает это уравнение каноническим. 2)из доказательства
теоремы ясно, что кривая, соответствующая уравнению*). Ах * + ТИЦ * ’\ — ДХ + ЕУ + Ф = 0、 Что это? а) LS = O парабола、 B) LS] > 0 эллипс、 в) преувеличение препарата<0. Например、)、 БД ^ + 7х-11 г + 6 = 0-парабола, данных AX4 + б / 4-20 * — гы + 8 = О-эллипс, 2jc * — Gy94 » 4 * + 12 лет проживает-7 = 0-гиперболические. ( * ) Предполагается, что формула (11) соответствует кривой, а не точке или паре линий и т. д. Это проще всего проверить, фактически преобразовав выражение (11) в каноническую форму. *Однако, чтобы
убедиться, что вы действительно обрабатываете кривые, показанные в этих примерах, вам нужно преобразовать записанные уравнения в их простейшую форму. Эта простая операция обеспечивает читателя. П°3. 2-е общее уравнение. Давайте вернемся к формуле (10). Теорема 3.Уравнение (10 )) Ax * — \ — Bxy + Cy * — \ — Dx + Ey + F = 0 Она
соответствует кривой, которая может быть эллипсом, параболой или гиперболой. Доказательство. Если B = 0, то есть если произведение xy не входит в уравнение, то мы уже доказали эту теорему. Предположим здесь ВΦ0.При повороте системы координат на произвольный угол δ уравнение(10) преобразуется в новое уравнение. Это новое уравнение показывает, что предыдущий угол 0 всегда может быть выбран так, чтобы не было члена, содержащего
произведение координат. Фактически в результате вращения системы координат старая координата (x, y) выражается в новой системе координат следующей формулой: х = ХХ cos0 —г \ Син 0; у = ХІ грех, потому что Замените x и y выражения (10) этими выражениями, чтобы получить выражение для кривой новой оси. А (,
потому что 0 —Йи Син 0)- ф — б (я потому что грех 0) (ЛК грех 0〜\ -ух Косинус 0)+ -Ф С (ХВ грех 0 + ух, потому что БФ + л = 0>(19) Где L обозначает совокупность всех остальных терминов. Понятно, что L не включает в себя 2-й член по отношению к xx. In в частности, L не включает продукт. запишем все члены формулы (19), включая x% Vy, отдельно. [- 2A sin 0 cos 0 + V (cos9 0-sin 90)+2Csin 0 cos 0] и позже 2sin
0 cos 0 = sin 20, cos90-sin9 0 = cos20、 Указанная группа членов может быть записана следующим образом [В COS 20-(л-с) грех 20] Xyyv Наша цель-выбрать такой угол 0, чтобы в Формуле (19) не было членов, содержащих произведение XYY. I cos 20-(Л-С) sin 20 = 0 (Л-с) грех 20 = потому что я 26、 Или наконец-то (21) Поскольку любое вещественное число действует как касательная к углу, всегда будет
существовать угол 0, удовлетворяющий соотношению (21) (для A, B, C).Но это также означает, что с помощью правильного вращения системы координат уравнение(10) всегда можно преобразовать в уравнение, не содержащее произведения координат. Замечание. 1) Если Λ= C, то уравнение (21) теряет свою meaning. In в этом случае он должен быть изменен на равенство (20). cos 20 = 0、 То есть cos 20 =
0 (ведь мы будем считать Bf 0).Однако это 20 = 90°, то есть 6 = 45°. Итак, при A = C нужно повернуть систему координат на 45°). 2) применяя метод доказательства теоремы к конкретному уравнению, мы можем сделать это уравнение каноническим. Однако существуют и более удобные методы для этой цели. Мы не будем
их рассматривать. (20 )) Или то же самое 3) по отношению к уравнению (10) возникают следующие критерии: кривая**) соответствует уравнению Топорик% + Ву + Су *-+ ДХ + ЕС + Ф = 0、 Я а) парабола при 4AC= B * t B) 4i4c> 5 *овал、 В) гипербола на 4 Это утверждение ничего не доказывает. в N°4.Образцы. Гипербола из-за асимптот. 1) рассмотрим уравнение 8x *-16 * + память+ 12y-4 =
0 Перепишите в форму 8С 1-2лг) + ЗСУ, — н > 0 = 4 Или дополните выражение в скобках до полного квадрата、 8 (f-2 * + 1)+ ЗСУ* + 4 >> + 4)= 24。 Отсюда (~!) ’. (y + 2) ’ 3 1 8 Перемещая начало координат в точку Oi (l, −2), мы делаем параллельный перенос системы. На новой оси уравнение линии имеет вид: 3 + 4- Он представляет собой эллипсоид с полу-оси Y3 и г-8.Этот трюк (новый! Обратите внимание,
что он находится на оси ординаты). 2) анализируйте более сложные примеры 4gv + 24hu + Tsu1-24kh-82u + 15 =0.(22) Начните с нахождения угла 0. Исчезновение произведения координат. Согласно (21) = Дж 482v = 4 ^ P = _T-123) Потому Что L = 4, B = 24, C = 11、 в pa 2tg6 О I A 2tg0 24 Итак, tgO — это 2-е уравнение^ _ q = — y или 12 tg90-7 tg 6-12 = 0. 4, 3.
Это уравнение удовлетворяет tg0 = -J и ТГ б= -. Неинтересно брать 0 из этих углов, потому что любой из этих углов удовлетворяет соотношению (23), но это все, что вам нужно. Возьмите по мере необходимости Угол 0 — это угол tg =0-.As [известно cos0 =± Так и в нашем случае cos0=:+=!(24)) И затем грех 0 = tg0cos0=± -^. (25) Выбор символов равенства (24) и, следовательно, (25) также свободен здесь. Конечно.、 Четыре если вы выберете tgO= -^, вы уже заявили,
что это гарантирует реализацию соотношения(23).Выберите Войти (24) cos 9 = 4. грех 0 = 4 ″» Формула преобразования координат при повороте системы на этот угол 0 принимает следующий вид: ДжейТи = а£л-4yLi у = у * У1. (26) Назначьте эти выражения выражению (22) в виде 4 }-y -1 bdg,-bu,+ 3 = 0.(27 )) Естественно, новое уравнение не включает в себя произведение. Выполните дальнейшие преобразования, как в предыдущем примере. То есть, напишите(27)
в виде: 4(}-4 * 1 + 4)-(y!+ 6y1 + 9)= 4 Или 1 4 Затем сделайте параллельный перенос системы и переместите начало координат в точку Oj (2, −3).Если вновь приобретенные оси обозначаются 0 \ X% и 0 ^ ur, то для xx = x2—2, yx = yb-3, а для оси 0 \ X^ уравнение прямой принимает вид: −1 т т т т Итак, эта линия является гиперболой
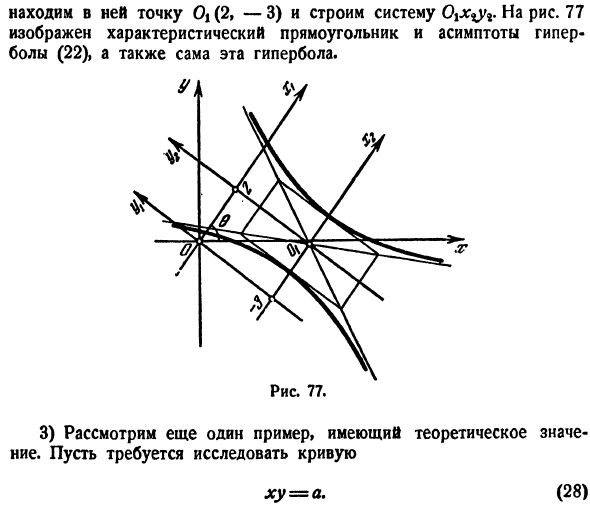
полуосей 1 и 2.Асимптотическая линия оси oijc| V имеет уравнение y1 =±2x%.Центром симметрии гиперболы является точка Oj. [В системе ohuh его координаты Xi = 2, yi =-3.So, согласно (26) системы Ohu, координаты точки 0\: = 3.6 и j»=-0.2. Чтобы нарисовать гиперболу на чертеже, сначала 3 4 поверните систему на угол cos0 = y, sin 6= -^ -. Этот угол находится в диапазоне от 0 до 90°и может быть легко настроен из тригонометрии известным способом. Если вы получаете
систему Ox / y / таким образом、 Найдите в нем точку Ot (2, −3) и постройте систему 77 Показаны характерные прямоугольники и асимптоты гиперболы(22), а также сама эта гипербола. 3) Рассмотрим другой пример, важный в теории. Нам нужно посмотреть на кривую. Ху = А. (28) Поскольку в этом уравнении A = C (=0), по замечаниям 1), система должна быть повернута на 45°.Для
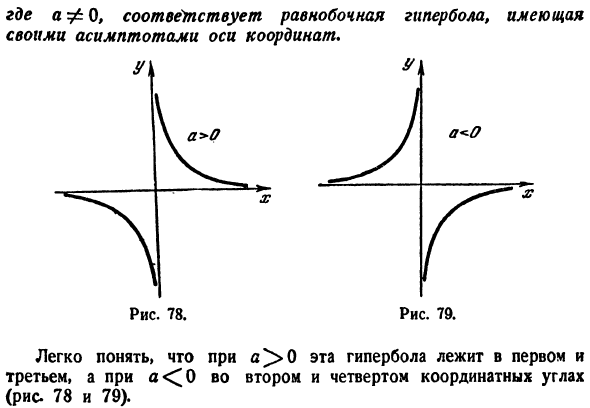
значения этого угла, равного 0, форма выражения преобразования координат имеет вид Если вы подставите эти выражения в (28)、 Си-ильный = 2а、 (29) (28) И это равносторонняя гипербола (в af 0).Его асимптоты делят пополам углы между осями симметрии. Но ось симметрии гиперболы (29) является новой! Это координатная ось, поэтому асимптота-это старая координатная ось. Таким образом,
теорема 4 доказана. Ху = А Здесь afO соответствует равносторонней гиперболе и имеет осевые асимптоты координатных осей. Это первая гипербола、 Если 3-й, 2-й и 4-й координатные углы равны 0(рис.78 и 79).
Смотрите также:
| Гипербола | Полярные координаты |
| Преобразование координат | Переменные и их пределы |

