Оглавление:










Диффузия вихря
Диффузия вихря. Важным примером нестационарного плоского движения в вязких жидкостях рассматривается диффузия линейных вихревых нитей. Предположим, что существует распределение скорости в первом moment. It расположена вдоль оси og и соответствует прямой вихревой нити с силой g. Итак, в проекции скорости на ось времени / = цилиндрические координаты r, 0, r имеет следующий смысл: 11, −0, = 2 r -«, =0. (16. 1) Необходимо определить движение жидкости в любое время после этого.
Смотрите также:
Этот ход, совершенно ясно, что vg и bx всегда равны нулю и r * * зависит только от r и/. В= УУ = 0, ВР = В (0. П-п (т, ф). Уравнение (5. 14) имеет вид дв / ДХ, 1 в почтовый индекс dg2 ~ ~ ’Т ДГ-7 *}’ Я собираюсь познакомить вас с вихрем скорости. Вт™ Г, ДГ. В § 8 мы вывели уравнение (8. 6). Это определяет изменение вихрей над time. In цилиндрические координаты, это уравнение имеет следующий вид: №. Д1 1 ДГ 1 г дБ ДГ * г ДГ В нашем случае, если v — 0 и 2 не зависят от 0, то это уравнение значительно упрощается.
Простое исследование показывает, что завихренность в данном месте возрастает с течением времени от нуля до максимума. Людмила Фирмаль
Однако ясно, что по (16. 3) (16. 4) будет продолжаться от (16. 2). В рассматриваемых начальных условиях уравнения (16. 2) или (16. 4) могут быть легко интегрированы с использованием соображений теории размерности. Например, ясно, что в уравнении (16. 4) функция 2, помимо переменных r и/, зависит только от 2 параметров v и γ, причем 2 прямо пропорциональны γ. So. .2 = ГФ (Р Л Г) .(16 .5 Запишите размеры всех величин, входящих в эту формулу.
Смотрите также:
Стационарное течение жидкости между двумя цилиндрами.
Если вы изменяете длину и единицы времени, уменьшая единицу времени на коэффициент T, длина r является фактором b, Число I является фактором T, а число 2 является фактором / T и так далее .Поэтому в новом блоке О гг / / 2х Г = — номера для некурящих [Н (м Если вы замените выражение здесь (16 .5) на 2, вы получите следующий идентификатор: Φ (Λ (, = (T I = — = и это выглядит так: Иначе говоря Так .. Предубеждения Вычислять: Теперь составьте уравнение. (16. 4), найти уравнение функции/ ($) легко.
Его также можно переписать в следующем виде: / + 4 / ’(5 + — [/(+ 4 / ’ (?) ] = 0 „Я / + 4 / Т) ] = С Но предполагая, что/ (=) и/ ’ (;) ; = 0 остаются конечными, поэтому, как вы можете видеть из предыдущего уравнения, вам нужно взять c = 0. Если положить 5 = 0 /(0 + 4 / ’(; = 0 Если мы интегрируем это уравнение, то получим: И / (5) =. 4 <* ч Где a-константа, которая должна быть determined. So. .Вычислим циркуляцию GL по радиусу β окружности вокруг начала координат .
Согласно формуле Стокса, существуют: Я .. Г “ = [2 ’21: П;С= [, -» гаг= 6 часов г-л / я * д =- с, В0 = 4М:ЛГ 1-Б’4*’). И2. Если я склоняюсь к k 0, потому что e 4y *также стремится к нулю Золото gl = 4-l g. 1 + 0. Но по условию, г / ч? = В первый момент g, следовательно (16. 7 Таким образом, мы, наконец, получили следующее решение проблемы. г. −4. Далее из равенства (16. 6) и (16. 7) следует следующая формула для циркуляции скорости по окружности радиуса r с центром в начале координат.
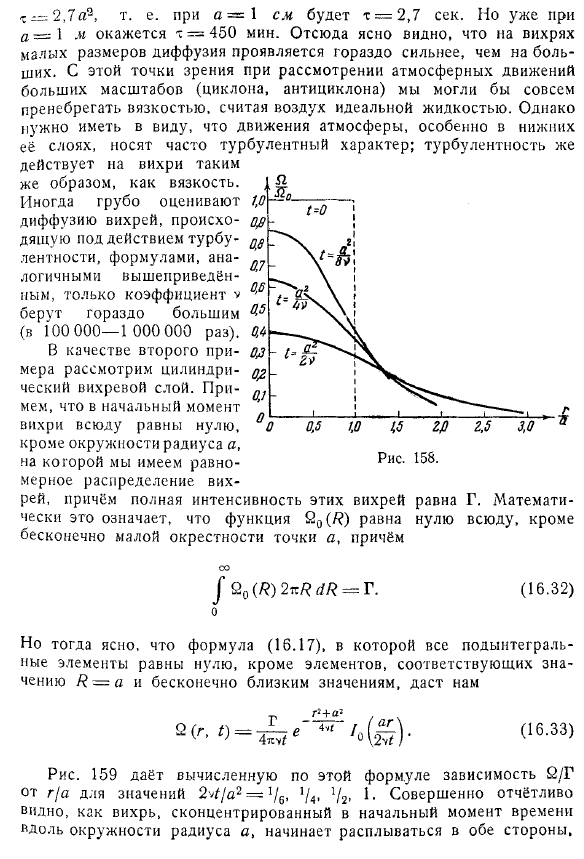
Однако, поскольку Гг = 2тг (16. 10 Однако вы можете легко проверить, непосредственно назначив, что функция (16l0) удовлетворяет выражению (16. 2). / — >Еще более ясно, что существует предельное равенство как 0 Убедитесь, что выполнены начальные условия (16. 1). Изучается решение задачи вихревой диффузии. Формула (16. 8) показывает, что вихрь концентрируется в первый момент в начале координат и с течением времени распространяется все больше и больше.
Этот факт показывает, как быстро затухает вихрь благодаря вязкости, которой он был обязан своим возникновением. Людмила Фирмаль
Однако ясно, что максимальная завихренность находится в том месте, где первоначально находился вихрь. Удаляясь от этого места, завихрения стремительно decreases. To характеризуя численно распространение вихря, находим радиус окружности, центрированной в начале координат, внутри которой содержится половина всех вихрей, то есть как радиус окружности r, циркуляция которой равна 1/2 g, изменяется со временем. Выражение (16. 9) указывает, что r должно определяться уравнением 1.
Смотрите также:
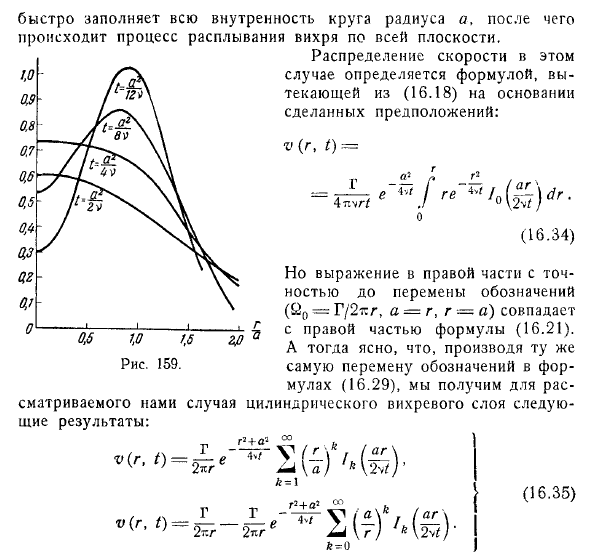
Затем он возвращается к нулю. Рассмотренный пример очень характерен для динамики вихревого движения вязкой жидкости. Он показывает, что основной тенденцией в вязкой жидкости является расположение вихрей различных частиц жидкости. Напротив, вблизи стенок, которые разграничивают жидкость, можно далее увидеть, что вязкая жидкость обладает замечательной вихреобразующей способностью по сравнению с идеальной жидкостью.
Рассмотренные нами проблемы могут быть весьма generalized. In другими словами, в уравнении (16. 1) вместо конкретного начального распределения скорости, соответствующего случаю концентрированного вихря, рассмотрим любое распределение скорости v начальной точки. Б (р, 0) = v0 в (Т). В этом случае начальное распределение вихрей задается формулой: 2 (Р, 0) = У0 (Н) = 1 <Р1. (16. 14) Но как будто я тебя видел

