Оглавление:




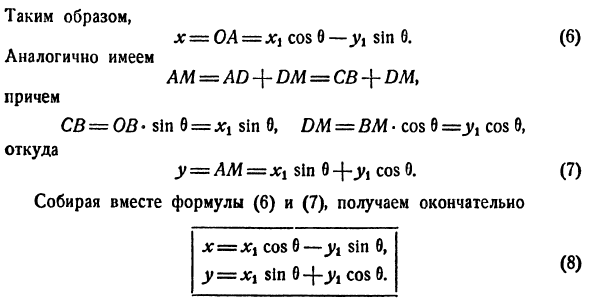







Преобразование координат
- Преобразование координат Н°1.Заявление о question. To записывая уравнения для линий, необходимо сначала выбрать определенную систему координат. Когда эта система изменяется, уравнение линии также изменяется. Например, если круг с радиусом & нарисован на плоскости, то выражение выбора любой системы координат будет
Вы можете видеть, что это уравнение особенно просто, когда начало координат сосредоточено на окружности. Поскольку a = b = 0 и уравнение (1) имеет вид Если вам удастся выбрать систему координат, вы увидите, что вы можете получить более простое уравнение для той же линии, чем если бы
иметь вид: (х-а)* +(г-БФ = Ф?。(1) Людмила Фирмаль
вы потерпели неудачу. Это еще более яркий пример влияния выбора системы координат на уравнение линии. Если на плоскости нарисована прямая линия, то выбор системы координат дает формулу: Ах + Ву + С = 0. (2) Однако, если это именно линия системы, которая действует как ось абсцисс, то уравнение для этой линии является: > =0.(3) Ясно, что (3) проще (2). Все это приводит к вопросу
о том, как упростить это уравнение, потому что оно имеет уравнение линий, которые находятся в определенной системе координат, и выбор системы координат более успешен. Чтобы решить эту задачу, сначала нужно выяснить, как меняются координаты отдельных точек при изменении системы координат. Здесь мы будем иметь дело именно с этой предварительной задачей. Сначала решите для
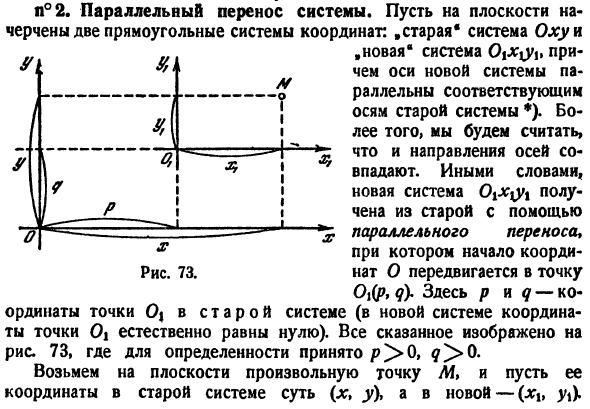
- 2 конкретных типов преобразований координат, а затем для общих случаев. н°2.Передача параллельной системы. Нарисуйте 2 декартовых системы на плоскости. Со старой системой * Ohu .новая * система 0 \ X \ yc и ось новой системы параллельна соответствующей оси старой системы*). кроме того, будем считать, что направления осей совпадают. То есть новая система-это квази *Где p и d-
координаты точек O старой системы, где начало координат O перемещается в точку Offa dU * где p и d-координаты точек O старой системы (в новой системе координаты точек O естественно равны нулю).Все вышеперечисленное показано на рисунке. 73, явно приемлемое место/?> О、 Возьмем любую точку/ U на плоскости, координаты в старой системе (x, y \и новой-(jct, y \ Я 4 1 1 -. а п — — — — — — г х, 1 ^ 1 1 г ——-— » Диаграмма 73. Вы можете увидеть 73 корреляции
непосредственно из диаграммы Х-Ху + р — > г = г \ + г. Людмила Фирмаль
Это означает, что в системе параллельного переноса старые координаты тонкого равны новым координатам и объединяются с теми же (старыми) координатами новой начальной точки. На первый взгляд более удобна формула, выражающая новые координаты в терминах старых координат, то есть формулы ХІ = х-ух пт = г-г, (5) Нам уже известно, что мы войдем в старые координаты, и нам придется искать новые.
Однако это не так, и Формула (4) более важна, чем(b). на практике мало нужно находить новые координаты точки со старыми координатами. Часто на основе.* Старое уравнение линии должно составить его. Новое уравнение. А для этого необходимо заменить старые координаты представлениями о старых уравнениях. То есть используйте Формулы(4), 5). П°3.Вращение системы. Рассмотрим
случай, когда новая система координат OhhUy взята из старой Ohu При повороте на определенный угол 0 (всегда отстает против часовой стрелки, и угол считается положительным). таким образом, обе системы имеют общую отправную точку O. As как уже упоминалось выше, предположим, что координаты точки M равны (x в старой системе и (xi9 yh) в новой системе. Из рисунка видно, что сторона этого угла перпендикулярна стороне угла, образованного осями Ox
и Oxu, поэтому она равна * AMB = b. х = ОА, Х \ = Обь, М = АМ, Ух = ВМ. Но… ОА = ОС-АС = ОС-ДБ. Сегмент OS и DB являются ножками прямоугольных треугольников OSV и MDB, первая из этих ножек принадлежит углу b, а вторая-противоположной стороне этого угла. Значение ОС = об * Косинус 0 = JCjcos 0, дБ = БМ * грех 0 = >> Исин 0. Поэтому, как хорошо、 Х = ОА = Х \, потому что грех б. АМ = АД + СД =
УП-\ — ДМ、 В дальнейшем СВ = ов * Sin b = XL Sino, DM= ВМ * COS 0 COS 9 Откуда j / = AM = jcj sin 0 + .Y1 Cos выражения (6) и (7) суммируют и, наконец, х = ХХ cos0-УБ грех 0, У = Х \ Син о + .У1 cos0. Чтобы запомнить эти выражения, рекомендуется отметить, что в Формуле x существует полная путаница*(перед Косинусом Знак, знак «минус»!), А в Формуле y означает «полный порядок» (знак перед Косинусом, знак «плюс»).
Выражение (8) дает представление старых координат относительно новых координат. Мы уже знаем, что нам очень нужно такое выражение. Если вы хотите представить новые координаты точки со старыми координатами, вам нужно найти xx и yt из Формулы (8) для этого. Если мы умножим их сначала на cos0, а затем умножим 2-й на sin 0、 xx = X cos0 — \ — y sin0.(9а) Аналогично, если умножить
первое уравнение (8) на sin 0, а затем вычесть из результата умножения 2-е уравнение (8) на cos0, то получится: г У = — Х Sin 0 — \ — г cos0.(96 )) Нет необходимости запоминать формулы (9).Формулу (8)следует запомнить, поскольку она играет важную роль в предстоящей презентации. в N°4.Общий случай преобразования координат. Наконец, рассмотрим общий случай преобразования
координат, когда системы Oxy (old) и Oixtii не совпадают ни с началом оси, ни с направлением. Используя ось Ox, угол b (рис. 75). Можно видеть, что этот общий случай легко сводится к тем случаям, которые уже были considered. To для этого введем другую систему координат в промежуточной системе координат 0 \ Xyt, которая имеет то же начало координат Oj, что и новая система координат OxXhukh *,
но параллельна осям OtX и 0 {старые координатные оси Ox и Oy. Понятно, что переход от старой системы Оху к новой Огхух может быть осуществлен в 2 этапа.1) произвести параллельный переход от старой системы Ohu к промежуточной системе 0 \ Hu, 2) повернуть систему от промежуточной системы 0 к новой Ohu-to Координаты (x, y), до точки имеет (.Если есть (X, y), (xit, y) t Х = Х + р, г = г + qт И формула(8) Х = Х \ cos0-грех, грех-0, Джей?= Jcj sin O + J’cicos 0,
наконец, оттуда x = xxcos0 — ^ sin 0 + / 7, = JfjSin 0-j — ^ jCOS 0 -} — Q. при p = d = 0 Эти выражения изменяются на формулу (8), а при 6 = 0-на Формулу (4). Н ’5.An алгебраическая кривая и ее order. It выше было доказано, что все прямые линии соответствуют линейным уравнениям. Это относится и к выбору системы координат. Таким образом, уравнение самой линии изменяется с изменением системы координат, но ее степень всегда остается неизменной. Точно так же, независимо от того, как вы выбираете систему координат, степень
уравнения круга остается 2-й. Суммируйте эти наблюдения. Кривая определения называется алгебраической, если она соответствует уравнению некоторой формы системы координат 4) (П) (12) (13)) Или 7xY + 2 * y + y » −10 = 0 x * + 2 * yv-3 = 0. Ахтуп + Bxlyh + Qtfyl 4 -… = о、 Здесь коэффициенты A, B, C,…Существует несколько (произвольных) вещественных чисел, а экспоненты m, n, f, ft, r, s,…
являются целым числом и неотрицательным числом. Примерами алгебраических кривых являются прямые линии, эллипсы, параболы и гиперболы. Алгебра — это, по крайней мере, кривая. Теорема. Если кривая имеет уравнение уравнения (I) в некоторой системе
координат Ohu, то в других системах Olxiyl она имеет такой же тип уравнения. Доказательство. Координаты любой точки M в системе Oxy (x, y), согласно формуле(10), представляются координатами системы Oixlyi (xlt y.). * » = » * !-VII в + р, г ^ медицины + уй ^ вопросы. Если точка M находится на прямой, то уравнение(11) справедливо для ее координат (x, y), его также можно переписать следующим образом:
А (у ХL-выти + П)М( «Г + ИИВТ ’+ г) п + + Б(э-э, — вык + п)(vxt + э + д)+… на 0.(14) Теперь откройте все скобки и сократите такие термины, чтобы преобразовать выражение (14) в форму Ну Жгу?1 + BrfM1 + …«=0, (15) Где коэффициент А1}Ви… И только индексы mitни ’и Numbers•••числа отличаются от (11).Однако тип выражения (15) будет таким же, как и выражение (I). Теорема доказана, так как уравнение (15) действует как уравнение для ряда новой системы. Грубо говоря,
смысл теоремы заключается в том, что свойство кривой, алгебраическое или нет, является внутренней характеристикой самой кривой, а не относительным положением этой кривой и результатом выбранной системы координат. Обратите внимание, что неалгебраические кривые называются трансцендентными кривыми. Такие вещи также известны, например, из хода среднейkкоды
синусоиды у = Sin * Или логарифмический г = 1 с GX. Вводится важное понятие порядка алгебраических кривых. Рассматривая выражение (11), мы различаем в нем термины AxmyMt ВХ * г * > Схну*%». Каждый из этих терминов имеет определенную степень. сумма показателей x и Y. Например, порядок члена AxMu *равен m + I. максимальная
степень различных членов уравнения (11) называется степенью этого уравнения. Например, степени уравнений(12) и(13) равны 5 и 7 соответственно. Теорема 2.Степень уравнения в алгебраической кривой одинакова для всех систем координат. Доказательство этой теоремы аналогично доказательству теоремы 1, но мы не будем останавливаться на этом подробно. Смысл этой теоремы заключается в том, что степень уравнения алгебраической кривой полностью
определяется не ее расположением относительно системы координат, а геометрическими свойствами этой кривой. Из-за этого вы можете классифицировать алгебраические кривые в соответствии со степенью уравнения, не беспокоясь о том, какая система координат назначена этим уравнениям to. In собственно, только эта теорема
оправдывает название. Например, по теореме 2, в любой системе координат•) эллипс имеет уравнение 2-го порядка, поэтому эллипс является 2-й кривой.
Смотрите также:
| Парабола | Упрощение уравнений кривых 2-го порядка |
| Гипербола | Полярные координаты |

