Оглавление:


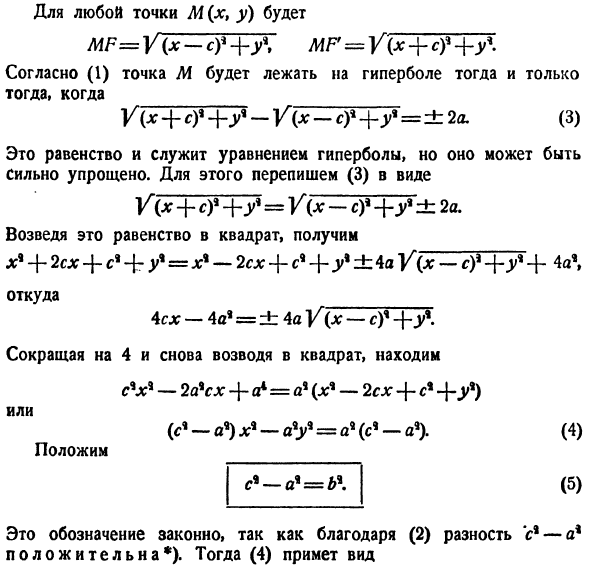











Гипербола
- Гипербола Н°1.Определение гиперболы. Его стандартное уравнение. Определение гиперболы очень похоже на определение эллипса. Наконец, слово. слово сумма*.просто замените на разницу. Определение гипербола-это линия, представляющая геометрическое положение точки, а разность расстояний от 2 заданных точек, называемая фокусной точкой, является постоянной величиной.
для любой точки M гиперболы существует 1 из уравнений. (1) МФ-МФ-жла. В этом случае знак M следует выбирать-или-в зависимости от точки, которая находится близко к фокусу F или F’. Да. Диаграмма 59. Точка M показана на рисунке,
Фокус обозначается F и F’, а вышеупомянутая разница обозначается 2n. Людмила Фирмаль
В равенстве (68) необходимо выбрать anak,+ * * если вы хотите указать фокусное расстояние FF через 2 секунды, как обычно ФФ-до н. э.、 В треугольнике MFF сторона FF должна быть больше, чем разница между сторонами MF и MF, поэтому она должна быть 2c ^> 2a. и так оно и есть.)、 (2) Чтобы найти гиперболическое уравнение,
необходимо сначала выбрать координату system. As в случае эллипса проведите ось Ox через фокус и поместите начало координат в середину сегмента FF (рис.59). 。 Для любой точки M (x, y) равно МФ = В(-С)* + у \ СЧ ^ данные + БФ + в *- Согласно (1), точка M находится на гиперболе. V (x + s) 9 + V-V (x-c?+ Г * =±2л(3) Это уравнение работает как гиперболическое уравнение, но оно может быть значительно simplified. To для этого перепишите (3) в следующем формате Г(х + с) *
- + пр-У(Х-с)*-\ — у * ±2a. By возводя это равенство、 dg9 + 2СХ + С9-ФК Г% — Х% — 2СХ + С9 + г * ±4а-с) + 4е1 Здесь._ 4cx-4а ’=±4а V (х-с)% + г Уменьшите до 4 и квадрат снова、 В-2А * СХ + А4 = А1(Х9-2sdg-Ф С4 + г) Или (С9-А9)* 9-в = А9(С9-А9). (4 )) Поставь П9-А9 = \Б(5) Это обозначение оправдано. Потому что, благодаря (2), разница с%-a9 положительна*). (4) принимает форму Это похоже
на эллиптическое уравнение. н°2.Изучение формы гиперболы. Установите форму гиперболы на основе уравнения(6).Уравнение включает в себя как x, так и y только в четных степенях, поэтому гипербола (6) симметрична относительно обеих осей. Поэтому достаточно выяснить форму только части гиперболы под первым
координатным углом. Для этого решим уравнение (6) относительно y. деление на A% b Людмила Фирмаль
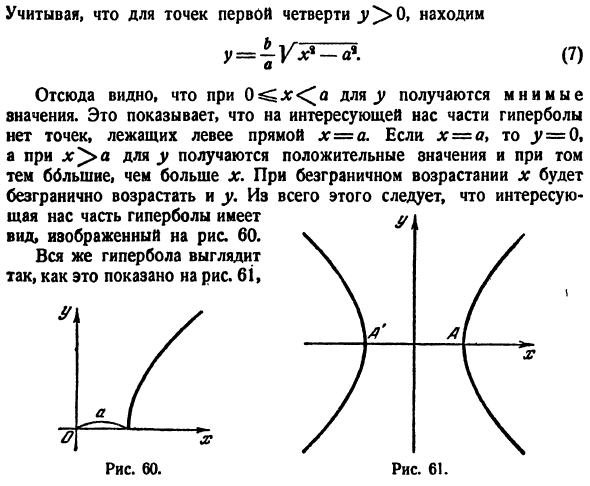
\ получаем каноническое гиперболическое уравнение (6) За первый квартал y> 0 баллов、 Г =(7) Это означает, что если 0 a, то получается положительное значение для y, и далее, x больше. когда x увеличивается неограниченно, y также увеличивается неограниченно. Из всего этого следует, что
интересующая нас часть гиперболы-это рисунок 260. Вся гипербола показана на рисунке. Шестьдесят один、 К Да. Диаграмма 60.Диаграмма 61. То есть она состоит из 2 отдельных частей, каждая из которых представляет собой бесконечную открытую кривую. Вышеупомянутая гипербола называется Бесс. Точки A и A ’являются вершинами гиперболы. Отрезок AA ’=
2a называется действительной осью гиперболы(6).Число a называется действительной полуосью гиперболы, а число b уравнения(6) называется полуосью этого мнимого числа. каковы геометрические значения B? это требуется в N°3. П°3.Асимптота Hyperbola. By вводя ключевое понятие асимптоты, мы получаем более точное понятие о форме гиперболы. Чтобы сделать эту тонкую концепцию более
понятной, давайте начнем с примера. Подумайте о линии Поскольку абсцисса x здесь только в квадрате, кривая симметрична относительно оси Oy. It это легко увидеть Потому что он расположен на оси быка. Для всех точек сделайте несколько точек, чтобы прояснить эту линию. если jc = 0, jf = 1; Если * = 0.5, то ^ = 0.8; если x = 1, d / = 0.5;если jc = 2, y = 0.2; если jc = 3, y = 0.1 и т. д. Кривая имеет вид,
показанный на рисунке. 62. когда x увеличивается, y decreases. In сложение, x( По мере того как ординаты * y становятся все меньше и меньше, они бесконечно приближаются к нулю. Однако, против всех X. поскольку г> 0 существует, ордината никогда не будет равна нулю. Поэтому точка движется вправо неограниченно вдоль кривой
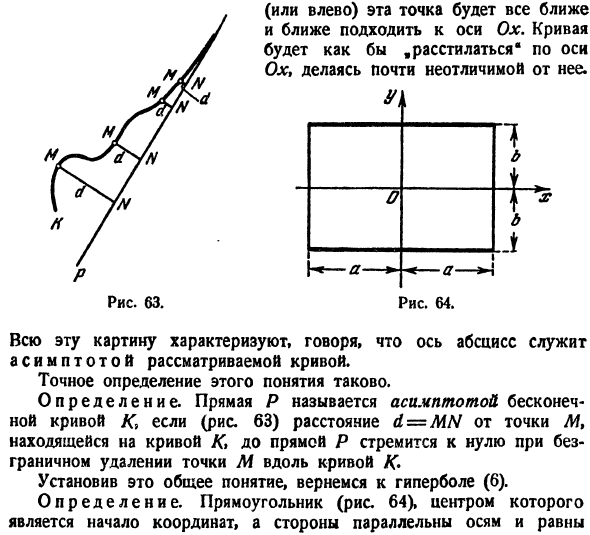
(Или слева) эта точка становится все ближе и ближе к оси Ox. Кривая «растекается» по оси Ox и становится почти неразличимой. + Т » о \ * БТ З — а — * — < — а— Рисунок 64. Вся эта картина характеризуется тем, что абсцисса является асимптотой рассматриваемой кривой. Точное определение этого понятия выглядит следующим образом:
определение прямая P называется асимптота бесконечного кривой к(рис. 63).Расстояние d = MN от точки M над кривой K до линии P равно нулю, когда точка K удаляется бесконечно вдоль кривой K. Установив это общее понятие, мы возвращаемся к гиперболе(6).Прямоугольник определения (рис. 64), его центром является начало координат, его стороны параллельны оси и равны Диаграмма 63. 2a и 2b,
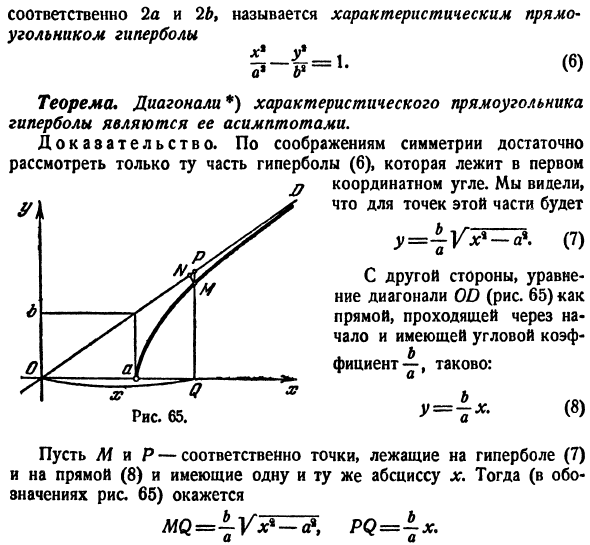
соответственно, называются гиперболическими характеристическими прямоугольниками Характерной прямоугольной теоремой гиперболы * диагонали* * является ее асимптота. Доказательство. По соображениям симметрии достаточно рассмотреть только ту часть гиперболы (6), которая
находится на первом месте. n-координатный угол. Я видел это. Суть этой части заключается в следующем B_a Диаграмма 65. Диагональное уравнение OD (рис.65), с другой стороны, выглядит следующим образом: прямая линия с квадратным коэффициентом через начальную точку. (8) Пусть M и P-точки На гиперболе (7) и прямой (8) соответственно с той же абсциссой X. Тогда получается
(в обозначении на рис. 65 МQ = — ЧХ * -а \ РQ = — х. Но、 Ввиду того, что Vx * — a4V ^ * = x}, ясно, что MQ ), Если вы не выполняете более подробно inspections.To поймите это, суммируйте разницу (9)、 * ) Конечно, речь идет о бесконечно протяженной диагонали. • * ) Ведь если мы знаем, что сумма r является разницей между 2 очень
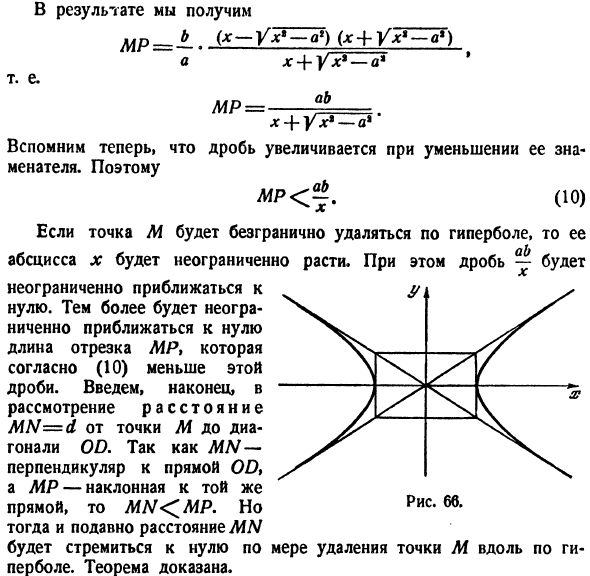
большими величинами A и B, то мы ничего не можем сказать об этом, так как r = A – B. Например, для 3000 LLC, B = 2 LLC, для R = 1,000,000,A = 3,600,000,B = 2,999,999. 98, р = 0.02. В результате、 х + стринги-а * аб Мистер= х + г ^ ZTai- Теперь вспомним, что дробь увеличивается при достижении знаменателя decreases.So … Да. (10 )) Н в В 1 2 Диаграмма 66. Если точка M удаляется бесконечно вдоль гиперболы、 Абсцисса х
возрастает до бесконечности.Фракции есть Приближение к нулю unlimited.In кроме того, длина отрезка MP, согласно (10), меньше этой доли и приближается к нулю до бесконечности.Наконец, введем расстояние MN = d от точки M до диагонали OD. Поскольку MN перпендикулярно линии OD, а MP наклонен к той же линии, MN <^
MP.Но дальше МН Когда точка M движется вдоль гиперболы, она стремится к нулю.Теорема доказана. Иначе говоря Формат — (8). Угловые коэффициенты 2-й асимптоты: Итак, уравнение гиперболических асимптот выглядит следующим образом (6): Б У = ТХ » г = — ТХ- Об этом надо помнить. При рисовании гиперболы на чертеже рекомендуется делать асимптоты на том же чертеже (рис.
66).Это позволит повысить точность.Попутно было выявлено и геометрическое значение мнимой оси гиперболы, определяющей высоту характерного прямоугольника. Уравнения для асимптот гиперболы Замечание.Наличие асимптот в гиперболе позволяет ответить на этот вопрос.В чем разница между гиперболической
ветвью и параболой?Представьте себе, что парабола уг * = 2rpx была нарисована в бесконечном поле, и на ней был создан высокий забор.Пусть зритель встанет на параболу и встанет спиной к Баору.Если он направит свой взгляд вдоль лучей y m = mx, отличных от оси Ox, он обязательно обратится к Джебу, потому что лучи yz ^ mx и парабола=пересекают не только точку начала координат. Но
поскольку qj=, я продолжаю поворачивать глаза т. В 1 Прямой линии (из-за дрожания мышц, управляющих глазным яблоком) это физиологически невозможно, поэтому забор виден перед ним, независимо от того, куда на самом деле смотрит наблюдатель.Поэтому ему кажется, что поле раскинулось перед ним и ограничено огромным овалом*). Зрителю представляется совершенно другая картина, стоя на этой гиперболе, спиной к забору,
построенному на гиперболе.Угол наклона к оси Ox асимптоты гиперболы равен 6.Если линия визирования наблюдателя находится под углом (по существу равным ей) большим, чем ось Ox и угол b, наблюдатель будет прислоняться к забору.Если этот угол меньше 6, то зритель увидит чистое поле зрения.Это означает, что поле зрения ограничено двумя прямыми вертикальными стенками, образующими
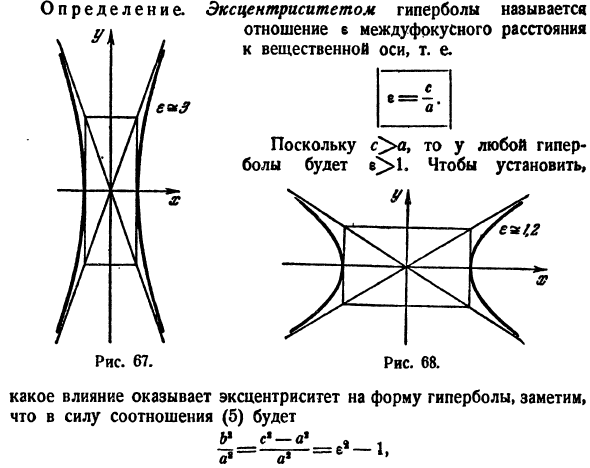
угол 2#. в N°4.Эксцентриситет гиперболы. Эксцентриситет гиперболы — это отношение е фокусного расстояния к реальной оси. Определение Диаграмма 67.Рисунок 68. Так как Oxi, гипербола становится e> 1.To установить Как эксцентриситет влияет на форму гиперболы, в зависимости от соотношения(5) Б * К-а. Откуда Это означает, что чем больше Е, тем больше угол решения между асимптотами. На рисунках 67 и 68 изображены гипербола, ee ^ 3 и tc *
1,2 соответственно. n°b. изометрическая гипербола. Определение если характерный прямоугольник гиперболы является квадратом (рис. 69), то гипербола называется равнобедренной плоскостью. Обратите внимание на 5 характеристик такой гиперболы. Они могут следовать непосредственно из этого определения, и каждое из них принимается за определение равносторонней гиперболы. Диаграмма 69. 1.In
равносторонняя гипербола, полукруги равны Или а = б. 2.Уравнение равносторонней гиперболической Формат — ^ — = 1 х *-^ = а 3.Асимптоты биссектрисной гиперболы перпендикулярны друг другу. 4.Существует уравнение для асимптот гиперболы изозида У = Х, У = — Х、 То есть угол между осями симметрии гиперболы уменьшается вдвое. 5.Эксцентриситет изозидной гиперболы 6 = 1 ^
2.In дело в том, что если a = b, то выражение c * = A% -\ — B% принимает вид c * = 2a\, за которым следует приведенное выше. н°б. Сопряженные Гиперболы. Если принять во внимание полное равенство осей Ox и Oy, то уравнение имеет вид Ноль ноль Соответствует гиперболе. Его фокус находится на оси Oy, реальная ось-2L9, мнимое число 2a. следовательно, характеристики
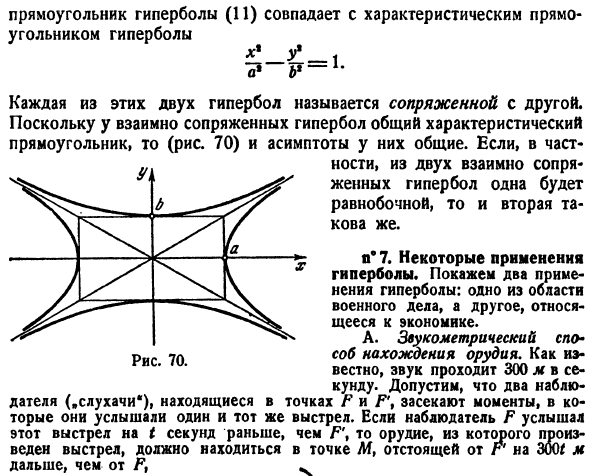
Прямоугольник гиперболы (11) совпадает с характерным прямоугольником гиперболы. Каждая из этих 2-х гипербол называется сопряженной друг с другом. Поскольку взаимно сопряженная гипербола имеет общий характерный прямоугольник (рис. 70), а ее асимптоты являются common. In в частности, если одна из 2 взаимно сопряженных гипербол равносторонняя, то 2-я такая же. И * 7.Некоторое использование Hyperbola. It показывает
2 использования гиперболы.1 относится к военной сфере, другой 1 связан с экономикой. A. Ядровый измеряя метод для того чтобы найти tool. As вы знаете, звук распространяется со скоростью 300 метров в секунду. Предположим, что 2 наблюдателя («слушателя») в точках F и F \обнаруживают момент, когда они слышат один
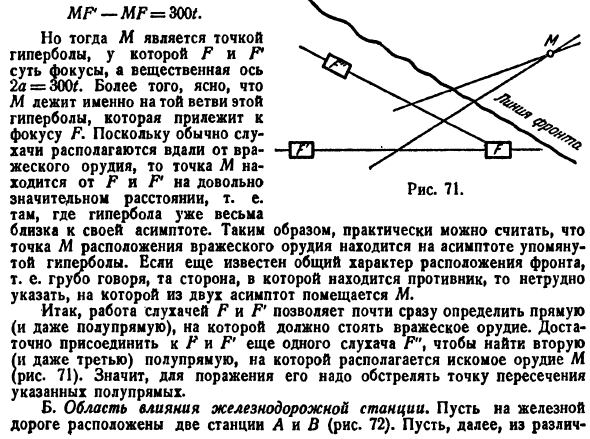
и тот же выстрел. Если наблюдатель услышал этот выстрел на f \ t секунд раньше, чем F \ t, то снаряд должен находиться в точке M, R на расстоянии 300 / м от F MF4-MF = 300 /. Но М является гиперболической точки, F и f находятся в центре внимания, и действительной осью является 2D = 300.Кроме того, понятно, что М точно находится в области бифуркации это гипербола, прилегающих
к очаговой Ф., поскольку судебное заседание, как правило, далеко от вражеской пушки, точка м находится на значительном расстоянии от F и F*.Гипербола уже совсем Близко к своему asymptote. So действительно, точку м положения орудия противника можно считать находящейся на асимптотах ранее упомянутой гиперболы. Общая характеристика положения линии фронта, то есть, грубо
говоря, если сторона, на которой находится противник, еще известна, то легко указать, какая из 2 асимптот АФ расположена. Таким образом, работы слушателей F и F ’позволяет практически сразу определить линию (луч), на котором вражеские пушки будут стоять. Для этого достаточно прикрепить другой слуховой аппарат F до f и F ’и найти 2-го (и 3) полуоси, где нужные пушки М находится (рис. 71). B.
пострадавшие районы железнодорожного вокзала. Предположим, что железная дорога имеет 2 станции A и B (рис.72).Далее, от Чрезвычайная ситуация Рис.71. Из точек местности, через которую проходит железная дорога, необходимо отправить груз в конечную точку дороги С. Мы считаем, что станция В находится ближе к точке с, чем станция А. проблема возникает естественным образом перед
грузоотправителем в точке АФ. Выгоднее доставлять товар автотранспортом для дальнейшей отправки по А или Б, железной дороге. Стоимость перевозки грузов определяется в рублях за 1 км при перевозке автомобильным транспортом, а в q-рублях за 1 км при перевозке железнодорожным транспортом. Далее перевозчик
производит следующие расчеты: 1) транспортные расходы по доставке товаров в (п-Ма + вопрос. АБ + г-до н. э.) рублей. 2) транспортные расходы по доставке товаров в г. {п-МБ + вопрос. До н. э.) рублей. Поэтому в Б выгоднее перевозить товары, которые находятся в точке АФ. p-MA + q * AB> r. MV или то же самое МА-МВ>-
<АБ (12)П Точка м из них(для них не имеет значения, где перевозить груз) АМ-АФ£«=с-J-АБ (13)) Диаграмма 72. Есть фокус A и B и лежат на гиперболе с реальной осью 2 а = Точнее, точки M, удовлетворяющие соотношению (13), находятся на ветви вышеупомянутой гиперболы, смежной с фокусом A*). таким образом, точка M, где (12) действительна, находится «снаружи» этой ветви(то есть на той части плоскости, которая отделена от точки A этой ветвью).
Смотрите также:
| Эллипс | Преобразование координат |
| Парабола | Упрощение уравнений кривых 2-го порядка |

