Парабола

Парабола

• Парабола n°1 * Определение параболы. Его стандартное уравнение. Определение парабола-это линия, представляющая геометрическое расположение определенной точки, называемой фокусом, и точки, одинаково удаленной от определенной линии, называемой директрисой. •) Эта речевая революция не очень accurate.

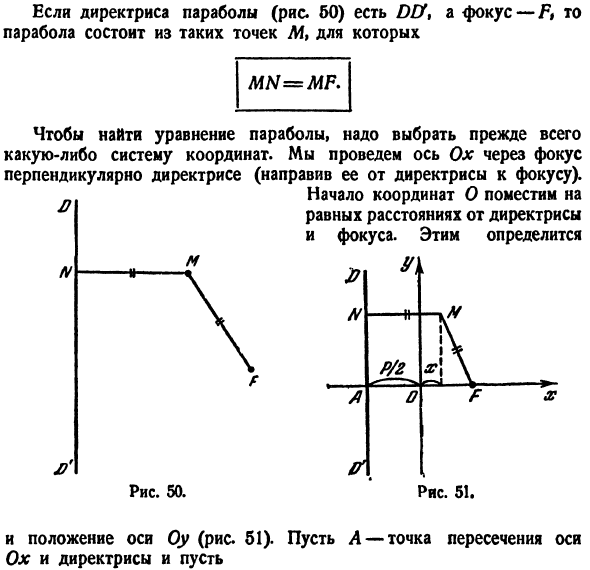
In фактически, y Свобода таких слов очень часто допускается(если не удается ввести в заблуждение）* Если директор параболы (рис. 60) — DU, а фокус-F», то парабола состоит из точки M и точки M MN = MF. Чтобы найти уравнение

= = 1x-это бесконечная прямая линия, и только ее конечный сегмент является диаметром эллипса. Людмила Фирмаль

параболы, необходимо сначала выбрать систему координат. Ось Ox рисует перпендикулярно к direclicks через фокус (от direclicks к фокусу). Расположите начало координат O на равном расстоянии от Директории и focus. It определяется Рисунок 50. Диаграмма 51. / В Л’ Положение оси OY(рис. 51). A-пересечение оси Ox и прямой линии、

АФ = п. Тогда координаты фокуса F будут^ y, Oj. Тогда возьмем любую точку M (x, y). понятно СЧ = г {-%) + г * С другой стороны, цифра ( * ) Точнее, для MW = | * + J вы можете легко установить его уравнением расстояния от точки до линии. Действительно, уравнение директрисы имеет Точка M находится на параболе только в том случае, если MF = MN>. Это равенство является параболическим

• equation. It это несколько громоздко. Для простоты Возведите это уравнение в квадрат. Когда вы открываете скобку, она выглядит так Или / = 2 пикселя. Это самое простое (или стандартное) уравнение параболы. Понятно, что это 0. н°2.Изучение формы параболы. Мы изучаем форму параболы, используя только уравнения г * =

2 пикселя,(1） Где: p> 0. Формула (1) содержит только 2-ю степень y. таким образом, парабола симметрична оси Ox, и для установления внешнего вида всей параболы достаточно установить форму части, расположенной над осью Ox. Для точек (x, y) эта часть будет y> 0, поэтому если вы найдете y из(1), то вам нужно поставить знак перед радикалом. Ноль） Это、 1) x не может быть отрицательным.

2) Если jc = 0, y = 0. 3) Людмила Фирмаль

В противном случае y будет воображаемым, потому что это смешно. Это означает, что на параболе слева от оси Oy нет точки.  Когда x увеличивается, y также увеличивается, и неограниченное увеличение x вызывает неограниченное увеличение y9, но не так быстро(например, когдаумножается на 4,

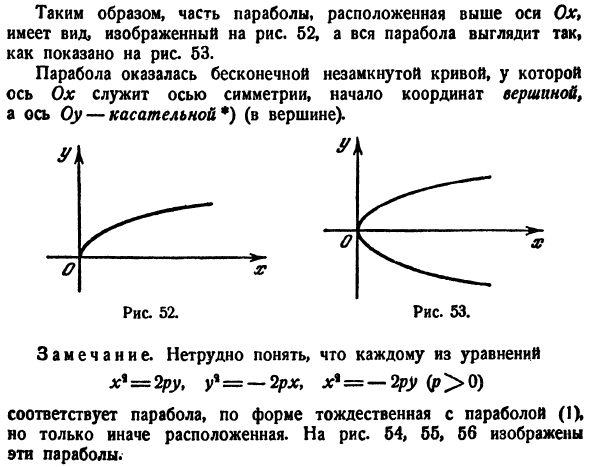
оно удваивается). икс+ вид =0.И так оно и есть.、 Минута= Y и+ о » Однако неточность текста не приводит к ошибке, поскольку вы описали уравнение MF = MN. Таким образом, часть параболы, расположенная выше оси Ox, имеет форму, показанную на рисунке 2. 52, и вся парабола выглядит так, как показано на рисунке. 53.

Получается, что парабола-это бесконечная открытая кривая, где ось Ox служит осью симметрии, где начало координат-вершина, а ось Oy-касательная) (вершина). Рисунок 52.Диаграмма 53. The remark. It легко понять для каждого из уравнений x * = 2p, y,= — 2px, x * = — 2p (p> 0 Он соответствует параболе и имеет ту же форму, что и парабола,

но только в разных положениях. На рисунках 54, 55 и 56 показаны эти параболы. 54.Рис.55.Рис.56. Образцы. 1) найти направление и фокус параболы с% = 6*.Здесь он равен 6 = 2p. следовательно, он равен p = b и служит фокусом И директрисой является прямая X =- 2) аналогично, если парабола xy = — 8y, то директор имеет y = 2 и фокус

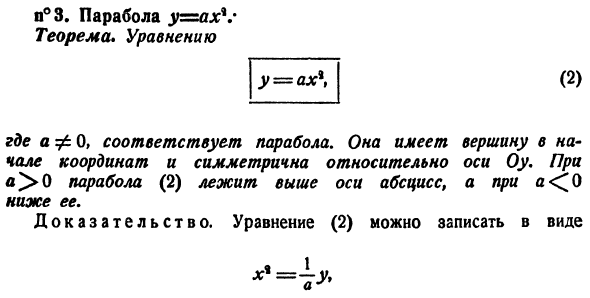
равен F (0, −2). Точное определение касательной указывается в секундах. Заболевание у = ах \ Где F 0 соответствует параболе. В начале координат находится вершина, симметричная относительно оси Oy. при n> 0 парабола(2) находится выше абсциссы, а при a <0-

ниже абсциссы. Доказательство. Формула (2)、 (2） П°3.Парабола y = теорема axV * уравнение Это уравнение вида x * = 2pu или x * = — 2pu (для 0), в зависимости от a> 0 или a <0.Последнее уравнение соответствует параболе, нарисованной в первом случае^. Рисунок 54, и Рисунок 5 2-й 56, если это необходимо. Чтобы выяснить, как форма параболы (2) влияет на модуль модуля Oy, мы покажем параболу

на рисунке 1 (рисунок 57). у = Х \ Точечная застройка Два * = =±1, х =±^ РТ Г = \ х \ Один и другой-2 абсциссы x = 0, 3, 2 младший===== =±：2.На этом рисунке видно, что чем больше абсолютное значение Of, тем ближе к оси Oy находится сторона параболы. (a> 0) чем выше a, тем круче парабола. Парабола имеет много применений для механики. Например, камень, брошенный по диагонали к горизонту, представляет собой параболу*). Диаграмма 57.

Смотрите также:

Предмет высшая математика

Прямая линия	Гипербола
Эллипс	Преобразование координат