Оглавление:








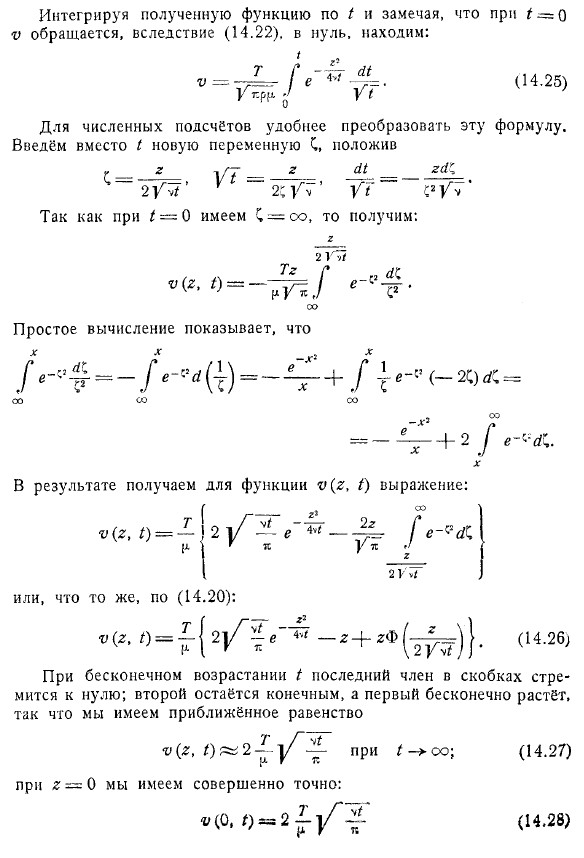


Нестационарное одномерное течение
Нестационарное одномерное течение. Подумайте об этом сейчас В случае вязкой жидкости движение более распространено, чем то, которое рассматривалось в предыдущем разделе. То есть он отбрасывает большое постоянство. Поэтому предположим, что движение вязкой, несжимаемой жидкости при отсутствии внешних сил происходит параллельно оси ox. Уравнение неразрывности показывает, что vi-не зависит от x.
Таким образом, уравнения механики жидкости значительно упрощаются. 1 доктор (02У, д2б ду д-р др р ДХ»v с ДУ * ДГ *) Ф ’«и* Из последнего уравнения видно, что p зависит только от x и (. Но в первом уравнении левая сторона не зависит от y и r, а правая сторона не зависит от x. So левая и правая стороны оба 1 функция( : / ( /) — Если 0, то уравнение v принимает вид: дю / d2u, dн> ДГ — ’я а? * «Т» д! * для f (*) φ0, введем новую функцию y вместо v.
Это уравнение является основным уравнением теории теплопроводности. Людмила Фирмаль
- Таким образом, V будет удовлетворять той же формуле (14 .3) .Правда, граничные условия несколько отличаются .Таким образом, во всех случаях нестационарного 1D течения мы сводим к интегралу уравнения (14 .3) . It известно, что она решает ряд специфических задач, связанных с этим уравнением, что позволяет определить большое количество соответствующих течений вязкой жидкости .
- Методические указания по гидромеханике
Конечно, при решении уравнения (14 .3) также необходимо учитывать соответствующие границы и начальные условия .Последняя будет указывать функции в начальный момент времени/ = 0 .Если и граничные, и начальные условия не зависят от координаты y, то решение уравнения (14 .3) V не зависит от y и удовлетворяет уравнению теплопроводности для функции y.
Смотрите также:
В задаче о морских течениях очень существенную роль играет отклоняющая сила вращения земли, которой мы в нашем примере пренебрегали. Людмила Фирмаль
Рассмотрим задачу о движении вязких жидкостей, занимающих все пространство, и рассмотрим распределение скорости B как начальный момент заданного известного выражения . 0) — = р (р) .(14 .6 Для закрепления уравнения (14 .5), можно применить метод Фурье .Другой способ-применить исходный метод .Во-первых, предположим, что функция Γ ненулевая только вблизи точки r.
Смотрите также:
Стационарное течение жидкости между двумя цилиндрами.
В этом случае ясно, что скорость V {r, () в какой-то момент будет функцией следующих 4 величин . ) = Φ (r, V, φ Кроме того, поскольку ясно, что V прямо пропорционально<3 г (р, 0 = (* .В.) Здесь мы применяем соображения размерной теории .Очевидно, что существует следующее измерение отдельных величин. Однако, функция должна удовлетворять выражению (14 .5).

