Оглавление:





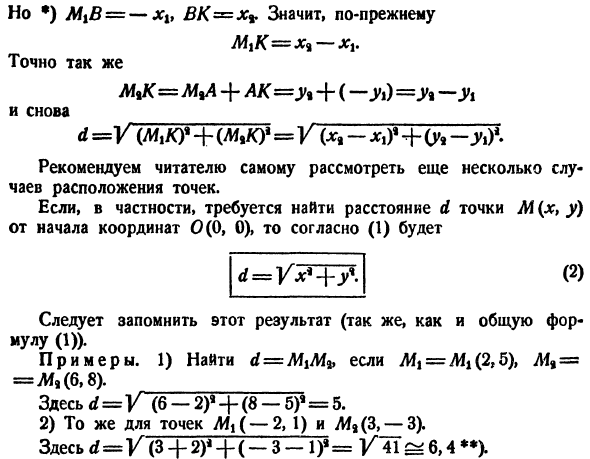








Точки и координаты
- Точки и координаты Н°1.Прямоугольная система координат » аналитическая геометрия-это область математики, которая изучает геометрические изображения с помощью Algebra. To сделайте это, сначала создайте несколько устройств, которые могут перевести геометрические понятия на алгебраический язык. Такое устройство было изобретено в 17 веке французским математиком П. Ферманом
и R. Is координатный метод, предложенный Декартом (П. ферма, 1601-1665; Р. Декарт, 1596-1650). Таких систем очень много. Знаком с так называемой прямоугольной) координатой system. At в конце этой главы мы введем еще 1 полярную систему координат.
Этот метод основан на нескольких предварительных понятиях-системах координат. Людмила Фирмаль
Нарисуйте на плоскости 2 перпендикулярные линии Ox и Oy (Рис.1).Обычно бык находится горизонтально, а Оу-вертикально. Эти линии называются координатными осями, где Ox — ось абсцисс, а Oy-ось ординат. Точка пересечения обеих осей называется началом координат. Теперь получаем произвольную точку M на плоскости (см.
Рис. 1), из которой отбрасываем перпендикуляры MA и MB на оси Ox и Oy. Поэтому отрезки OA и OB отделены от оси. Интересуясь длиной этих отрезков, покажите некоторые признаки. Подбор букв осуществляется по следующим правилам: Рисунок 1. Правила. 1) Если точка A находится на оси Ox справа от точки O, то знак присваивается длине OA-если j — ••A находится слева от O, то знак я — \присваивается длине OA 2) Если точка B находится на оси Oy
- выше (ниже) точки O, то знак^ j — •(знак, —) присваивается длине отрезка OB. На рисунке оси Oh и Oy обычно имеют стрелки, которые напоминают вам о правилах этого знака. Длины отрезков OA и OB, полученных с указанным знаком, обозначаются соответственно x и Y. х = ОА, у = Обь X-абсцисса точки M и y-ордината этой точки. Общее
название хны-координаты точки М). C at 4 3 2 / i — — — — — — n£ 1 ю? — /O −7 −3 / 2, f 14 5 6 x in Рисунок 2. тот факт, что число xnu является координатой точки M>, описывается как M(x, y).Зная координаты точки М, легко понять, как построить эту точку: необходимо отложить отрезки ОА и ОВ на оси Ox и Oy(направление, в котором обозначены знаки x и y), и расположить их перпендикулярно осям A и B, их пересечение — точка M. Пример A (3,2), B (4, −1), C(-2、5)、£)
(-3、-2)、£(4、0)、F(0, −2 ) Решение проиллюстрировано на рисунке. 2. Людмила Фирмаль
Обратите внимание, что точки на горизонтальной оси (ордината) имеют нулевую ординату (абсциссу).Начало координат имеет координаты(0, 0). Все вышесказанное можно резюмировать в следующей форме: Первый принцип соответствия* 2 числа
соответствуют любой точке на плоскости, то есть координатам. И наоборот, все пары чисел соответствуют определенным точкам плоскости с этими числами в их координатах. Вместо того, чтобы говорить «найти координаты * „или“ указать координаты* » и т. д., он просто говорит » найти«, » дать«и т. н°2. Расстояние между
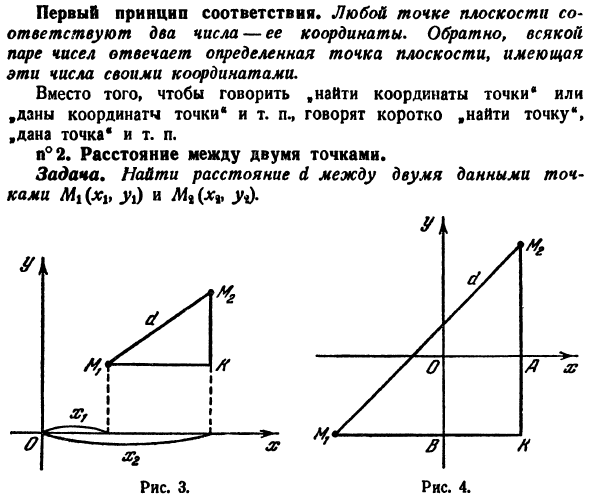
2 точками. Проблема. 2 данные точки Mi (xv ударов и Mg( Решение. На рисунке 3 показано, что искомое расстояние действует как гипотенуза прямоугольного треугольника MtKMтаким образом、 Но тот же рисунок показывает это Мик = х% — ХЛ МГК = г% — г . Ноль) Значение д = Дэ-ХТФ в + Обь-ytf. Эта формула решает проблему. Замечание. Уравнение (1) было получено с учетом простейшего
расположения Mx и M, как показано на рисунке 1.Однако Формула (1) применяется к расположению Afj и M%.Давайте хотя бы рассмотрим случай, показанный на рисунке. 4.Здесь.%11K = M’1B + VK. Но * M ^ B = — xv BK = x *так как раньше МТК = х% — ХВ. Точно так же МТК = МФА + АК = г%+(- г,|)= г-г、 А потом еще раз д = В (мм ’+(а *./ 0а = В(^ а-+(г,-г \ г *
Читателю самому рекомендуется рассмотреть несколько примеров расположения точек. В частности, если необходимо найти расстояние d точки M (x} y) от начала координат 0 (0, 0), то согласно (1) (2) д = ЧХ * + г \ Этот результат следует запомнить (как и общую формулу (1)). Образцы. 1) Если d = M \ M < » Afj = Mi (2.5), M * = Mg(6.8). Где d = Y (6-2) f +(8-5) 1 = 5. 2) то же самое верно для обратного (-2, 1) и M% (3, −3).
Здесь d = V(3 4-2)1 +(-3-1)* = V ’ 41 s * 6.4 3) найти точку м на оси OY на расстоянии D = B от точки N (3,7). Поскольку M находится на оси Oy, абсцисса x точки M равна 0.Остается найти ординату y. но условие MN = b по Формуле(1) V (3-0) 4 +(7-следовательно (7-y)* = 16, 7-yy =±4,A = 3,yy = 11. Так что есть 2 решения для этого problem. It это Mt (0.3) и M *
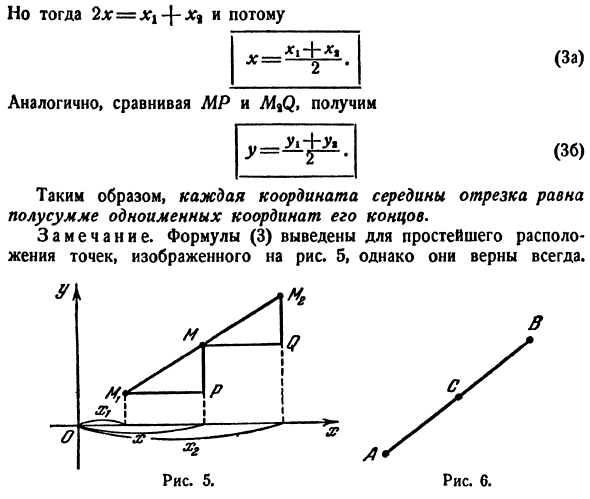
(0.11). П°3.Среднего сегмента. Проблема. Даны точки (jc» j.) и Л1а (jc», j> 9).Найти M (x, y)в середине отрезка MiM%. Решение. Создайте треугольники MVPM и MQM *, показанные на рисунке. b. It понятно, что они равны друг другу. Поэтому, в частности、 MiP = MQ Или то же самое Х Х \ — — Х ^ — Х• Аналогично, при сравнении MP и M%Q、 v_U1 — \ — ой Таким образом, каждая координата в центре отрезка равна
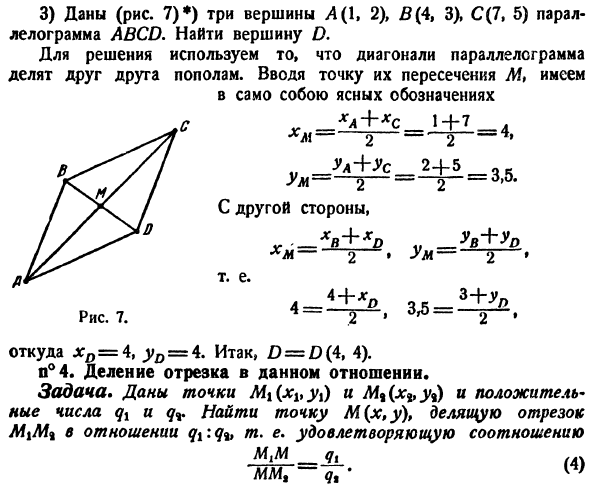
полусумме одноименных координат на его концах. Замечание. Уравнение (3) выведено для простейшего расположения точек, показанного на рисунке. 5, но они всегда верны. (36) Но 2x = Xi — \ — Xi поэтому、 (Для) 5. 6. Образцы. 1) Λ=Λ(5、2)、5 = 5(11、8)в этом случае, найти с (х, у) отрезку АВ (рис. 6)*). (3) согласно、 8, y = * ± * — = 5, C = C(8.5). 2) найти конец B, так как мы знаем конец A (2, 3)
и середину C (4, 9) отрезка A. Пусть B = B (xv, uv). (3) согласно、 ХД + х УА + УВ Хз-2 Нас-2 ′ 4 i±fe t-2″ » −2«、 откуда xv = 6,> ^ = 15, то есть B = B(6, 15). 3) даны (рис. 7)*) 3 вершины параллелограмма ABCD A (1, 2), B(4, 3), C(7, 5).Найти пик D. Для решения задачи используйте тот факт, что диагонали параллелограмма разделены пополам друг
с другом. Если вы введете эти пересечения M、 На понятном языке CL + * C 1 + 7 Иначе говоря 7. Ум.—- 2-2 С другой стороны、 。 ХС + хD УФ + УО хмм = — yM = JLTJl> 3 + г н Хм. Ул + США = 2 + б = <=!+ X и- откуда x)= 4, yD =4.Следовательно,£> = D (4,4). в N°4.Разделение сегмента на это. Проблема. Да. Ммш-qт ’ западной долготы Решение. Создайте
треугольники M% PM и MQM, показанные на рисунке. 8.It понятно, что эти треугольники являются similar. So … МЮ > _ _ МТМ МQ—мм7 ′ Но… MiP-X-xlt MQ = xh-x из этого и(4) х-х%_ Я.• Поэтому Точно так же ХВ— х-xxq%= х%тип qy-xqx Эти формулы относительно трудоемки, но если обратить внимание на то, что нужно умножить
координаты каждой точки кормы и М9 на число, соответствующее отрезку, то запомнить будет проще. Заметим, что формула (5) справедлива для любого расположения точек Mi и Mi, а также указанных на рисунке. 8. В частности, для ql = q%= gt формула (b) изменяется на ранее выведенную Формулу(3), которая дает
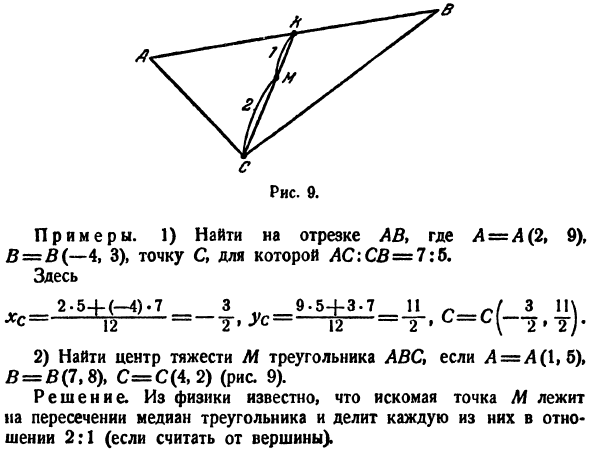
координаты середины отрезка. 9. Образцы. 1) Найдите отрезок AB. A= A (2, 9), B = B (-4, 3), точка C, AC: CB = 7: 6. Здесь. 2-5 +(-4).7 3 9-5 + 3-7 11 g 3 11 \ * С=-12—Т ’У* —12 — = \ 2′ −2) 2) Если A = A ( \ , b), B = B (7.8), C = C (4.2), найти центроид M треугольника ABC(рис.9). Решение. Из физики известно, что искомая точка M находится на пересечении медианы треугольников, деля каждый на отношение 2: 1(если
считать сверху). Когда вы найдете точку K, разделите отрезок SK на соотношение 2:1 _ «2 + 13_g с з » а- И так оно и есть.、44 =((4、5)。 н°б. Площадь треугольника* Проблема. Данная точка-Mg (Xi^) * m% (x * y&[Mg (l **, yy)).Найти площадь F треугольника M \ M% M * Решение. Опустите перпендикуляр от точки MiM%, М9 к оси Ox (рис.10).В результате получается следующий рисунок * C * 1 + Xk ’ 2 48 = 4 м Пусть K-центр стороны AB. И затем… 6.5. = 1 + 1 = 4, УК = ул + г * = в + * = Домой. Этот » дом «состоит из трапеции AiMiM ^
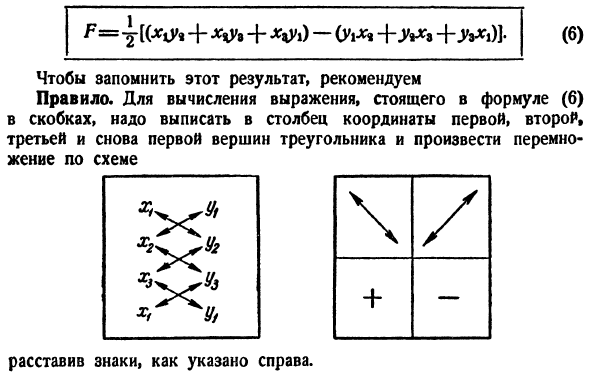
A% и Agmtmmiav, а интересующий треугольник получается путем удаления трапеции aimimtat из»дома«.Значение Рисунок 10. Х (•«-• * )—С «- Если мы расширим скобки и дадим аналогичный термин、 Чтобы запомнить этот результат, мы рекомендуем rule. To вычислите формулу в скобках в формуле (6), опишите координаты 1-й, 2-й, 3-й и 1-й вершин треугольника в столбце и умножьте их согласно схеме \ / ±
Поместите знаки, как показано справа. Образцы. Вершина(2、1)、(8、3)、(6、5)Найдите площадь треугольника с помощью Решение. Создайте столбец, который вы обсуждали. 2 1 Икс 8, 3. Икс 6/5 2×1 И затем… /. ’=±[(2.3 + 8.5 + 6.1)〜(b8 + 3-6 + 5-2)] = 8 квадратных единиц Замечание. 1) иногда формула(6) дает F
отрицательное значение).После этого знак минус отбрасывается. 2) если вычислить F по уравнению (6), то F = 0.Это означает, что точка Mi, M^, находится на 1 Прямой линии. Дай Правила. Чтобы узнать, находятся ли 3 заданные точки На 1 Прямой линии, используйте рис.> c Необходимо принять их за вершины треугольника и найти их площадь F. Если F= 0, то точка лежит на 1 Прямой. Образцы.
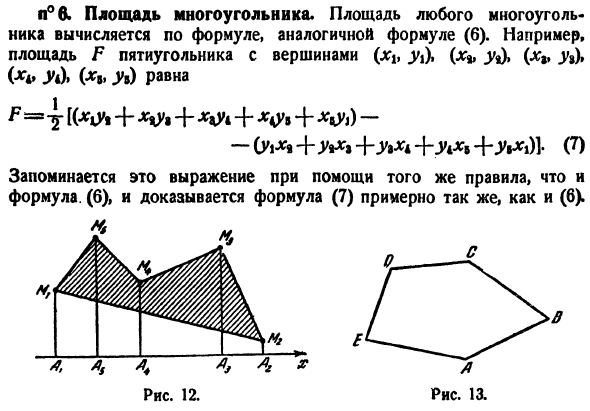
Выясните, находятся ли точки A (1, 12), B (5, 6) и C (9, 0) на 1 Прямой. Решение. Создайте столбец. 1-12 Икс 5 б. Х[(1.64-5-0 + 9.12)-(12-5 + 6.9 + 0.1)= 0。 9 0 Л 1×12 Так как F = 0, AB, C находятся на одной линии. Л°6.Площадь полигона. Площадь полигона вычисляется по формуле, аналогичной формуле(6).Например, площадь F пятиугольника
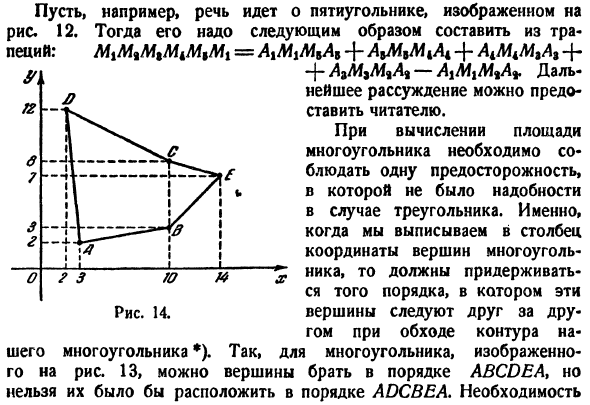
с вершиной (х% (х%, (ХГ, гг)>> * * уд (•»У*) является、 ^ ык * Л + Х%г * + х * г * > + х <г * ± -(Ил + г * си г — \ — йхб(7) Это выражение сохраняется с использованием тех же правил, что и выражение. (6), а уравнение (7) доказывается примерно так же, как и (6). 13. 12. Например, предположим, что речь идет о Пентагоне, показанном на рисунке 12.Тогда tra-Mimimtmmt = Ayma,+ L5LMM4 + AkMkMgAg-f- — Ф-
AlM9M%АБ-AiMtM ^ АФ. Читатель может обсудить дальше. При вычислении площади многоугольника необходимо соблюдать 1 меру предосторожности, которая не была необходима в случае треугольника. То есть при записи координат вершин многоугольника в столбик необходимо соблюдать порядок следования этих вершин
друг за другом при сканировании контура многоугольника*).Поэтому для полигонов, показанных на рисунке 13, вершины могут быть получены в порядке ABCDEA, но не в порядке ADCBEA. Необходимость Рис.14. С этой предосторожностью расчет площади полигона следует
начинать с создания хотя бы чернового чертежа. Образцы. Вершины A(3, 2), B(10, 3), C (10, 8), D(2、12)、£(14、7)Найдите район Пентагона по адресу. Решение. Начнем с построения вершин
фигуры. 14.Если соединить их прямыми отрезками, то можно увидеть, что порядок ABCDEA неприемлем. Возможный порядок-это, например, ABECDA. Если записать координаты вершин, взятых в таком порядке, в столбец、 3 2 10 3 10 8 ^ = tK9+ 70 + 112 + 120 + 4>- 2 12-(20+ 42+ 70+ 16 4-36)] = 65.5 квадрат. Единицы 3 2
Смотрите также:
| Решение невырожденных линейных систем. формулы крамера | Линии и уравнения |
| Решение систем линейных уравнений. теорема Кронекера-Капелли | Прямая линия |

