Леммы о бесконечно малых

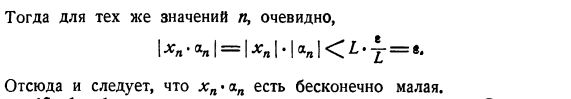
Леммы о бесконечно малых

Леммы о бесконечно малых. В следующей теореме 2 переменные(или более) рассматриваются одновременно и объединяются со знаком арифметики operations. In в этом случае, как уже упоминалось выше, эти символы приписываются соответствующим значениям переменных. Например, сумма 2 переменных xn и yn>, которые выполняются отдельно от последовательности значений、 •「」 «^1 » Х%> ХВ> И затем Йи Г *> Г * Уя> .

Сумма бесконечно малых конечных чисел это также бесконечно малые величины. Людмила Фирмаль

• Переменная xn > yn означает принимать последовательность значений Х3 \ У3…. хп + УП… В доказательстве теоремы, связанной с результатом арифметических операций над переменными, помогут следующие 2 леммы о бесконечно малых. Лемма.

• Выполните доказательство в случае 2-х мизерных и (а также исчерпанных в обычном случае). Любое число e]> 0 равно given. By определение Бесконечно малые, бесконечно малые, бесконечно малые Это число LG, где η>будет Существует. Я-мой ^ −2 * Такого количества л «’、 Аналогично, для бесконечно малых pl, η> Если вы хотите использовать положительное целое число N, используйте оба числа/ V ’и/ V’.в случае η> N.

Потому что эти неравенства выполняются одновременно. Людмила Фирмаль

• 1-й + Rl1 ^ 1al | + 1MS_2 + 2’:=: = e * Следовательно, количество Ма-| возьмем все значения n м ^ хп ^ м \ М\, \ М \ > Км ^ хп ^ М ^ 1 или| Х | Ц/,. Учитывая любое число е> 0, существует число на число Y на бесконечно малую、 Тогда, для очевидно того же значения, очевидно、 Я хп ’»л = я= Я х я * я ап я ^ ^ * х=! Из этого мы можем видеть, что xn * an бесконечно мал.

Смотрите также:

Решение задач по математическому анализу

Распространение на случай функции от произвольной переменной.	Арифметические операции над переменными.
Предельный переход в равенстве и неравенстве.	Неопределенные выражения.