Элементарные функции

Элементарные функции

Элементарные функции. ВВот список некоторых классов функций, называемых элементами. 1°.Рациональные функции целого и дробей. Функция, выраженная в виде целого числа относительно буквы x полиномом у = А1> хп -) А1 <П-1 + …/объявление (Йо, а, ай… Константа) называется целой рациональной функцией. Такое отношение 2 полиномов АО * л 4-Д»** «1 +•••4Dd-1 * od Г + bxx ^ −1 + … + bt_xx + БТ Представляет собой дробное рациональное число function.

Он определяется для всех значений в x, за исключением значений, которые обнуляют знаменатель. Людмила Фирмаль

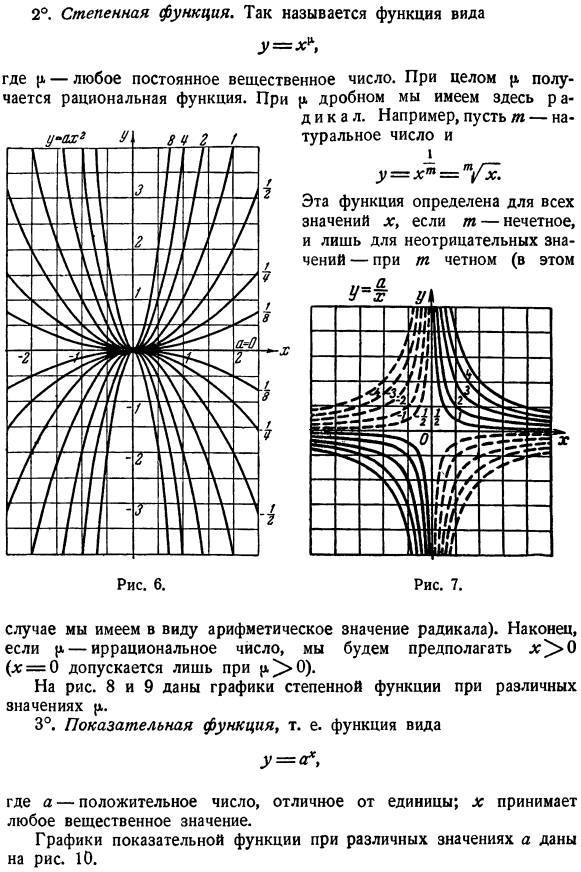
• Рисунок пример На рисунке 6 показан график функции y = ax9 (парабола) для различных значений фактора a. 7-график функции y = −2. (Изобарная гипербола) также в различных значениях. 2°.Функция питания. так называемые функции Если это означает арифметическое значение радикала).Наконец, (предполагая, что x; = 0 допускается только для (x]]> 0), если x иррационален. На рисунках 8 и 9 представлены графики функций, приводящих в действие различные значения p. 3°.

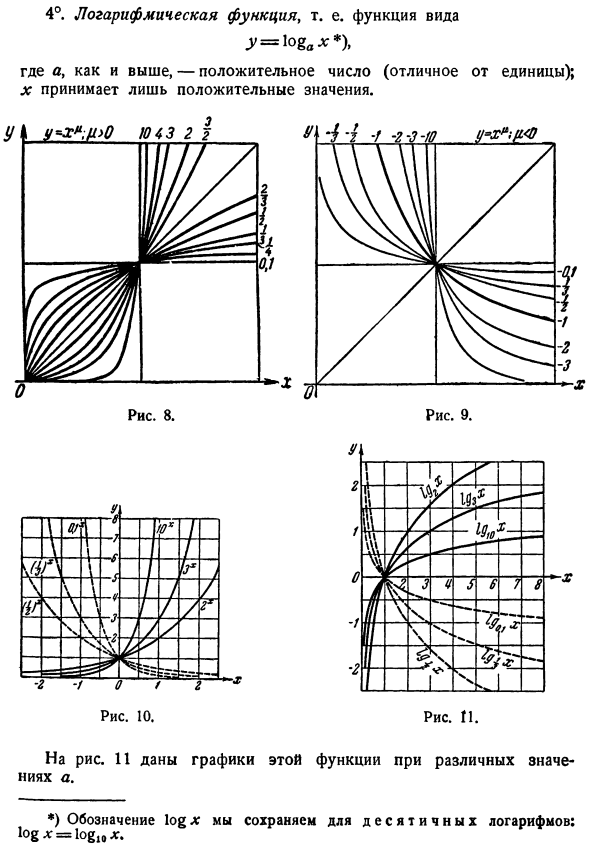
• Экспоненциальная функция, то есть функция вида Г-0х、 Где A-положительное число, отличное от 1. х принимает действительные значения. на рисунке показан график экспоненциальной функции различных значений a. 10. 4°.Логарифмическая функция, то есть функция вида г = \ о%ах *）、 Здесь, как упоминалось выше, а-положительное число (отличное от единицы). X принимает только положительные значения. На рисунке 11 показан график этой функции для различных значений a. * ) 10 шестнадцатеричных обозначений оставить 1o ^ x:1О8* =1О&,,.. 5°.

Синусоидальный график обычно называют синусоидальной волной. Людмила Фирмаль

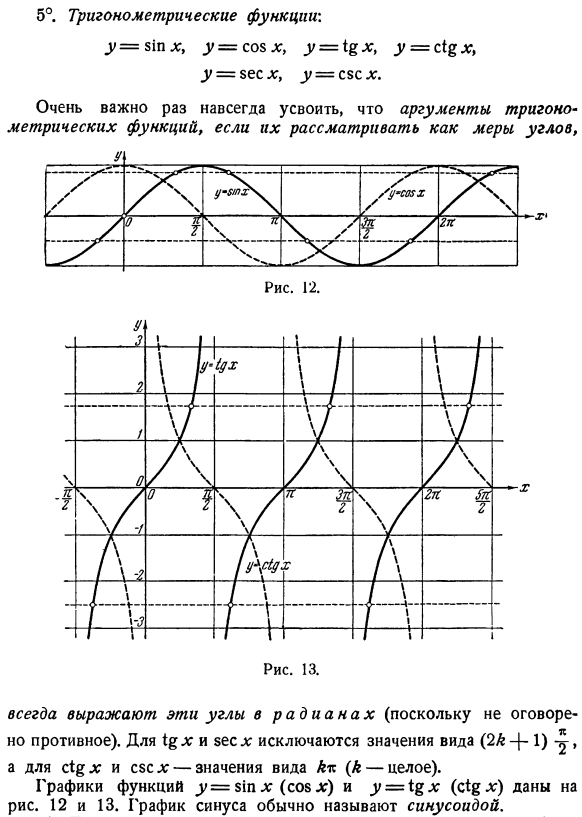
• Тригонометрическая функция： г = ЗТЛ:, г = со $ х, у = 1%х, г = С1 $ х, у = $ ехх, у = c8xx. Очень важно сразу понять, что аргумент тригонометрической функции, если, считается мерой угла. Эти углы всегда представлены радианами (потому что противоположное не указано). Для 1 ^и zesls исключаются значения в формате (2A +1) ^ 1 для c * $ le и sccl значение в виде Ats (где A-целое число). График функций y = ztx (cosx) и y = X% x (c ^ n) показан на рисунке. 12 и 13.

Смотрите также:

Решение задач по математическому анализу

График функции.	Понятие обратной функции.
Функции натурального аргумента.	Обратные тригонометрические функции.