Оглавление:


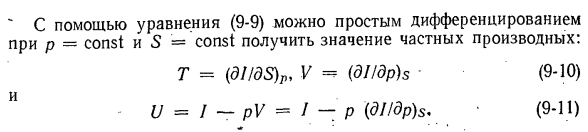






Свойства характеристических функций
- Характеристика функциональные характеристики Как видно из вышесказанного, второй закон термодинамики может быть применен для решения различных конкретных задач. Однако метод анализа исследований, основанный на рассмотрении специальных функций государства, называемых характеристическими функциями, также оказался полезным. Характеристическая функция состояния-
это функция, которая через производные различных порядков может выражать все термодинамические свойства системы, состояния, удельную теплоту Cp и Cy, а также термодинамический потенциал(см. ниже).К характеристическим функциям относятся внутренняя энергия u (V, S), энтальпия/(p, 5), изотермический потенциал F (7 \ V), изобарный
включая уравнения, определяющие уравнение Людмила Фирмаль
Z (p, Г), энтропия 5 (Vy U), объем V(5, U). Поэтому, если знать аналитическое представление этих функций независимыми параметрами системы, то можно получить в явном виде все основные термодинамические величины, характеризующие эту систему. Характеристическая функция является аддитивной. Значение
сложной системы равно сумме значений этих функций отдельных частей. Производная характеристической функции является совершенной производной. На основе уравнений первого и второго законов термодинамики получено уравнение, объединяющее оба закона. Tds = dU + pdV. (9-1) Как известно из предыдущего изложения, это выражение называется термодинамическим identity. It относится
- к обратимым процессам, содержащим только параметры, функции состояния системы, их различия. Для переменных p и T термодинамическое тождество(9-1) принимает вид: ТДС = дл-ВДП. ■(9-2)) Уравнения(9-1)и(9-2) являются наиболее распространенными уравнениями термодинамики. Они связывают между собой 5 переменных величин: величины T, S, U, ru V, которые определяют состояние системы. Из этих 5 параметров можно настроить
комбинацию из 10 различных пар. U, T \ U, 5; U, p1, U, K; 7 \ S \ TU V; 7 \ p; 5; p; S, V \ p, V. из них только 4 имеют большое значение для термодинамических исследований. U = U(5, V) — внутренняя энергия; 1 = 1 (5, p) — энтальпия; • Ф ф(в Тай)-изометрическая изотермического потенциала; з-з(т, р) — Внутренняя энергия U является характеристической функцией независимых переменных 5 и V. Если система выполняет
изобарный изотермический и изобарный потенциал. Людмила Фирмаль
свою работу, то формула изменения внутренней энергии принимает вид: ду-ТДС-ПДВ. (9-3)) Используя уравнение (9-3), вы можете просто дифференцировать V-const и S = const. Т =(ду / ДС) в \ р =- (dWdV) с ’ (9-4) И затем… / =И+ pV = V-V (dU / dV) s. (9-5)) Вы можете определить коэффициент калорийности, получив 2-ю производную от < U (S, V)>. (д * ЕД / DS2 у) и V =(ДТ / ДС) в = т(ДТ / ТДС) в * * Т(dTidq) в = Т / резюме、 Откуда Резюме: — — -. (9-6) «(А2 < / / а») в в Из Формулы(9-4) можно увидеть следующее: •(d2U / dV2) s =(dpidV) s. Исходя из уравнения (9-4),
параметры взаимно дифференцируются. д *и (ДТ \ Д * Е / ДП в / о-7 \ dSdV Уравняйте квадратичную производную, и вы найдете так называемое отношение Максвелла. — (ДП / ДС) и V =(dTldV) S или (ДС / ДП) в =-(ДВ / ДТ) С. (9-8). Энтальпия/является характеристической функцией независимых переменных 5 и P. Когда Дана формула (9-2) 、 dl = TdS + VdP. 。 (9-9) «Используя уравнение (9-9), мы можем просто дифференцировать p = const и S = const, чтобы получить значение
частного дифференциала. Т =(ди / ДП)Р, V =(дл / ДФ•(9-10) У = / п = / — р (диджей / ДП) с (9-11) Основываясь на уравнении (9-10), мы строим смешанную 2-ю производную от/и выравниваем их аналогично(9-8), чтобы получить 2-е отношение Максвелла. (ДТ / ДП) с =(дв / ДС) P или (dpIdT) с(ДС / дв) стр. (9-12)) Кроме того, производная 5-го порядка от p = const может определять Cp по формуле (9-6). (dT / dS) p =(d2I / dS2) p, но dqp = cpdTp = TdSp、 Или (ДТ! ДС) П = Т / Ср. Отсюда СР =(d4jdS>) Р ’(9
и3) Если переменными являются температура и объем, то изометрически-изотермический потенциал становится характеристической функцией, смысл этого названия раскрывается из подробного описания. Если вычесть d (TS) из правой и левой частей уравнения (9-1)、 дю-д(ц)-= ТДС-ПДВ-д (ТС); г (п-ц)= ТДС-ПДВ-ТДС-СДТ(9-14) И затем ДФ = д(у-ц)—СДТ-ПДВ (9-15) Откуда dF = d (U-TS) или F = U-TS. (9-16) Некоторое количество TS, также являющееся
функцией состояния, иногда называют энергией связи (см.§ 9-2). Из Формулы(9-45) простой дифференциал с T = const и V = const позволяет получить значения других параметров. Ы = _(ДФ / ДТ) в; р =- (ДФ / DV) Т (9-17) U = F + TS = F-T (dF! ДТ) Т (9-18) I = U — \ — pV = F — \ — Ts + pV = F-T (dF / dT) v-V (dF / dV) T. из (9-19) 2-го уравнения(9-17) мы можем получить тепловое состояние equation. In фактически,
мы получаем p = p (K, T), потому что F выражается в V и T9, то есть F = F (V, T). На основе уравнения (9-17) построим смешанную 2-ю производную функции F, уравним их и получим 3-е отношение Максвелла. (доктор! ДТ) г-(ДС / дв) Р. (9-20) В экспериментальных исследованиях изометрический изотермический потенциал
V7 полезен тем, что независимые переменные V и Γ легко доступны для измерения. Производные 2-го порядка функций F (V, T) относительно T и V позволяют определить удельную теплоту CVS. Используйте формулу(9-17). — (ДС / ДТ) V с =(«.Для. ч ч < — — — з—>- ТДС-дю — + pdVv ДС = — г-х-р-г-1 НМ I
Смотрите также:
Решение задач по термодинамике
| О неправильных обобщениях Клаузиуса в вопросе о возрастании энтропии | Физический смысл изохорно-изотерлжого и изобарно-изотермного потенциалов |
| Среднеинтегральная температура | Химический потенциал |

