Оглавление:


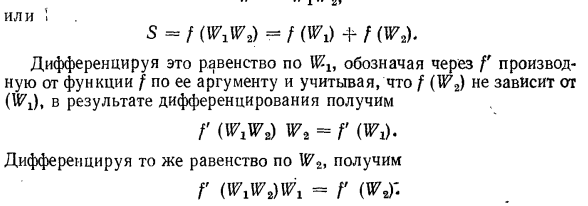




Энтропия и статистический характер второго закона термодинамики
- Энтропия и статистические свойства второго закона термодинамики В конце XIX в. Многие ученые(Максвелл, Больцман, Гиббс, Смолуховский и др.) доказали в своих исследованиях, что второй закон термодинамики не является абсолютным естественным законом, а только связан с макропроцессами и не применим к Микросистемам. Больцман дал статистическую интерпретацию второго закона и отметил ограниченность его применимости. Проще
говоря, теорию Больцмана можно резюмировать следующим образом: Предположим, что есть кровеносные сосуды, которые мысленно делятся на 2 части: правую и левую. Допустим, у нас есть 1 молекула в этом контейнере.* сосуда составляет 50% или 1/2, поскольку с такой же вероятностью ом может находиться и на левой стороне. Если в контейнере находятся 2 молекулы, то вероятность 2 независимых друг от друга событий выражается как произведение
Вероятность нахождения этой молекулы на правой стороне Людмила Фирмаль
обеих отдельных вероятностей, так что вероятность 2 молекул, находящихся одновременно справа от контейнера, не равна.(1/2)-(1/2)= 1/4 。 если в контейнере находится n молекул, то вероятность их одновременного присутствия в правой части контейнера четко выражается дробью: Р = 1/2 /、 Учитывая, что даже небольшое количество газа состоит из огромного количества молекул, можно сказать, что вероятность нахождения этого большого количества
молекул только в одной части сосуда близка к нулю. Все спонтанные процессы, которые переходят из состояния низкой вероятности в состояние высокой вероятности, необратимы и связаны с повышенной энтропией. Следовательно, должна существовать связь между увеличением энтропии системы и переходом из маловероятного состояния в вероятное. Максимальное значение
- энтропии соответствует устойчивому равновесию системы. Это наиболее вероятное условие при определенных условиях. Таким образом, энтропия 5 адиабатической системы должна быть функцией термодинамической вероятности W *ее состояния. 5 = /(Ш). ■ Предположим, что система разделена на 2 части. Часть энтропии I! И S2) вероятности для этих состояний равны Wx и W2 \энтропии,
а вероятности для всей системы равны 5 и С основной позиции Больцмана это выглядит так: Ст = /(Жо; С2 = Ф \ w2y, с = / м. То есть энтропия системы равна сумме энтропий отдельных частей. S = Sx-r S $、 А вероятность состояния системы равна произведению вероятности отдельных частей: Вт = W1W2t » 1 с Ил 5-/(УТО = /(WX с)+ ф(В2). По / указывает
Энтропия системы обладает свойством аддитивности. Людмила Фирмаль
производную функции f относительно ее аргумента и различает это равенство с учетом того, что f не зависит от (Wi).в результате производной (|)、 Р («да W * = р т. Если вы дифференцируете одно и то же уравнение、 G (WXW2)WX = G (WJ- Первое полученное уравнение умножается на Wlt, а второе-на W2.Левая сторона обоих уравнений будет равна, поэтому правая сторона будет равна. •* ф ’(ш ^ ж,= /’(WX с) Мас \ т(В. В.) Р м мас = р ш Поскольку части системы
полностью произвольны и состоят из любого*, последнее уравнение является ВФ(Вт)= ку Где k-постоянная Болдмана. e. 1 универсальная газовая постоянная, присвоенная одной молекуле. Из соотношения S = f (W)、 Если мы сравним последние 2 уравнения、 управление конфигурацией-к ДГ ~ Ш 9 После интеграции, откуда S = k в W + C Полученное уравнение является уравнением Больцмана, которое
связывает энтропию системы и вероятность ее состояния. Энтропия s замкнутой системы в равновесном и неравновесном состоянии пропорциональна натуральному логарифму вероятности этого состояния. Так, формулировка 2-го закона термодинамики Больцмана: «изменения состояния системы происходят спонтанно только в том направлении, в котором каждая часть системы переходит
от распределения с меньшей вероятностью к более вероятному.」 Поэтому Больцман показал, что увеличение энтропии нельзя считать абсолютным. Больцман впервые отметил статистическую и относительную природу второго закона термодинамики. Он продемонстрировал не только увеличение энтропии природы, но и радикальный потенциал ее уменьшения (например, за счет
флуктуаций). 。 Но, несмотря на прогрессивный характер идей Больцмана, им необходимо указать на свои слабые места. Больцман предполагал абсолютное равновесие мировой системы, при котором отклонения происходят случайным образом в определенных местах Вселенной. Вы не можете согласиться с этим. Энгельс из»диалектики природы»отмечал, что»с точки зрения диалектического материализма все процессы во Вселенной суть процессы бесконечного и непрерывного саморазвития материи.»
Смотрите также:
Решение задач по термодинамике

