Погрешность квадратурных формул

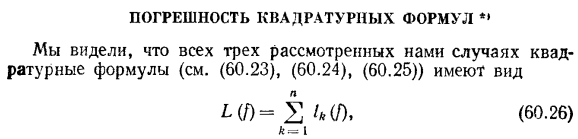
Погрешность квадратурных формул

Погрешность квадратурных формул. Во всех рассмотренных 3 случаях квадратурая обнаружил, что существует формат для в этот момент. М. следуйте идеям, разработанным в монографии Николь! «Ортогональный.» М. Это был 1974. 559. Где же он? (60.27） 60.5.Ошибка в квадратуре* И p-это некоторые числа. Для прямоугольного выражения、 −0, РО-1 ″ Случай трапециевидной формулы Здесь задается некоторое числовое значение p/, называемое весами, и система точек i = 0, 1, называемая узлами…, так что m задается в интервале[0, 1]. как и прежде, отрезок[a, b] имеет точки xk, k = 0, 1,…N равных отрезков по n[Λ * _1, xk \ k = 1, 2,…предположим, что он разделен на n., сегмент[0, 1], сегмент[xk.. получить точки из узла b путем линейного отображения на [B xk].

Все квадратурные формулы (60.26) обладают свойством линейности. Людмила Фирмаль

• Здесь нулевая точка перемещается в точку π * _1 (т. е. отображение x =(xk-xk-y) 1 + xk-1, 0 * e ^ == e1. Формула (60.26) в этом случае является узлом H и Весами ri 1 = 0, 1,…называется квадратурой, соответствующей т. Р (В + М)= РР(/)+ \ ХВ {§). н Формула определения b ([) −2 1k(!Не является к = 1 Для полиномов степени r, для полиномов степени P (x) степени под r, для любого отрезка[i, b]и любого числа n (то есть деления на равные отрезки отрезков[a, b]) получается равенство. Б Б (п (х))= \ п (х) 1х Но… Любые 2 функции f и g, определенные интервалом[a, b], d, любые 2 числа H и p, очевидно Упражнение. Узел и вес p, докажите, что квадратурная формула B [[], соответствующая 1 = 0, 1 m, точна {60.

Некоторые вопросы для приблизительной оценки Пятьсот шестьдесят Для полиномов степени r необходимо и достаточно, чтобы полином p (x) степени, равной или меньшей r, был равен. 1 ТР \ P ( ’ • ’) Ox = 2 P1p (1d » 1 = 0 Интерполяционный многочлен степени r равен многочлену степени r. Уравнения прямоугольника, трапеции и Симпсона корректны для многочленов степеней 0, 1 и 2 соответственно. Однако, кроме того, ортогональные уравнения прямоугольника точны для многочленов 1-го порядка, а уравнение Симпсона точно для многочленов 3-го порядка. Давайте докажем it. In факт, в случае■2Г4-7ХН + ХС, прямоугольное уравнение (см. (60.23)） 2 (60.27）） Рис-240 к(/)= f (^ r ^) (*xk1). Простой расчет дает уравнение для любой линейной функции HK 1k (Ax + B)= ^(Лх + в) (1х.(60.28)） ХК-1 Это хорошо видно на рисунке. 240.

• Суммируя уравнение для k в 1-n(60.28), получаем: б В0 (Ах—Ь)= ^(Ах—Б) ЛК、 Но… Для официального случая Симпсона (см. (60.25) и (60.27)） kφ=■^ [| /(ХК-Р）+1 | /（、）]。 (60.29)） В этом случае достаточно указать любой многочлен P (x) в 3-м порядке. HK k (P ( * )) = \ P (x) dx, k = 1, 2 p(60.30） ХК-1 На самом деле, если эти равенства доказаны, если вы суммируете их по k от 1 до n、 б И (P ( * )) = \ p (x) xx、 Но… 60.5.Ошибка в квадратурной формуле 561. То есть уравнение Симпсона точно для полинома 3-го порядка. Пусть P(х)= Ax3 | информацию bx2 + СХ + О.(^(х) 0,П(Х) = Ax3 * 0.(икс.)И так оно и есть.、 Ф *(Р(х))= А1к(Х3) \ 1к((НХ））、 HK в Гонконге $ P (x) yx = A ^ x3dx \ IΦ (x) yx, k-1, 2,… С. (60.31） ХК-1 ХК-1 ХК 1

Потому что уравнение Симпсона точно для полинома 2-го порядка、 HK Lk (Φ ( * )) = ^ 2 (x) dx, k = 1, 2,…н. HK-1 С другой стороны, по прямому расчету、 4-1 + 4 в, 41 2 I + 6〜 Гонконга 4-4-1 1к(Х3)=(ХК-ХК-1) [^-1 + 4 Это доказывает равенство(60.30). Вы можете видеть, что степень ошибки четырехугольников связана со степенью полинома, в котором рассматриваемые четырехугольники являются правильными. Предположим, что функция теоремы f непрерывна дифференцируема на интервале[a, b \и что число 0 0 равно: | / ^® (x) 1 <Λ1, и x b. б | /（）/-/.(/） см (б-А) Р + 1 ′ ~ ~ / т (60.32） Если ортонормированная формула (60.26) имеет порядок r-1(r = 1, 2,…Существует константа cc-0, которая не зависит от функции/если она верна для многочлена Доказательство.

Это означает точность квадратурной формулы полиномиального прямоугольника 1-го порядка. Людмила Фирмаль

• Функция/представлена следующей формулой для каждого сегмента[xk-1, xb\, и Taylor]: Где же он? G-1 ПМ = 1р -^(Х-Хк-хУ 1 = 0 НХ)= ПК(х)+ ГК(х), к = 1, 2,…н.、 562. Поскольку это многочлен Тейлора степени r-1, rk (x) является остаточным членом уравнения Тейлора и записывается в Лагранжевой форме. 。 /, г [ * -! + б *(х-ХК-д] ■(х-ху-ГУ、 0 6А 1, м-1.2 / г; R и(Х)= И затем… \ ХХ) ух-У)= 2 5 /(х) УГ-2 / *(/) = (60.33） к = 1П = 2 Один А = 1 ^ ПК(х)УГ-1к(ПК(х）） 1. + 2 Один + 5 g *(x) Фх-1к {RK (x）） к-1 (60.34)） § 60.Некоторые вопросы для приблизительной оценки Поскольку эта квадратура точна для полинома R-1 порядка, уравнение *） ^ ПК(х), УГ-1к(РК(х))= 0,к = 1, 2,…、 л * −1 Г(х)ых-б(д） 2 5 | р *(х) / топор+ 2 | / *(р *(х)) [. (60.35） к = 1 х к-1 к-1 Таким образом, из(60.34).

Смотрите также:

Решение задач по математическому анализу

Интерполяция функций.	Приближенное вычисление производных.
Квадратурные формулы.	Разбиение множества на классы эквивалентных элементов.