Квадратурные формулы

Оглавление:

Квадратурные формулы

Квадратурные формулы. Теперь рассмотрим несколько способов аппроксимации функции. Формула для приближенного значения Интеграла называется ортогональной формулой. Дайте функцию/в виде интервала[a, b].Отрезок [a, b]точек xk, k-1, 2,…разделите его на N равных частей на n-1. С = Х0 Х1… XYA_1 XYA = b; xk-xk-1=^^, k = 1, 2,…н. Когда вы интегрируете функцию/с каждым интервалом[xk-b xk], вы можете заменить ее интерполяционным полиномом степени N. вы получаете квадратурную формулу для рассмотрения. рассмотрим случай n= 0, 1, 2/, N ( / ), n = 0, 1, 2.In в первом случае (если n = 0) соответствующая квадратурная формула называется прямоугольной формулой, а во втором («=!«))Параболическая формула, или чаще формула Симпсона. Прямоугольное выражение Функция / интервал[x * 1, xk], k = 1, 2,… …1 узел.

Для интерполяции в n достаточно указать только многочлены с нулевой степенью. Людмила Фирмаль

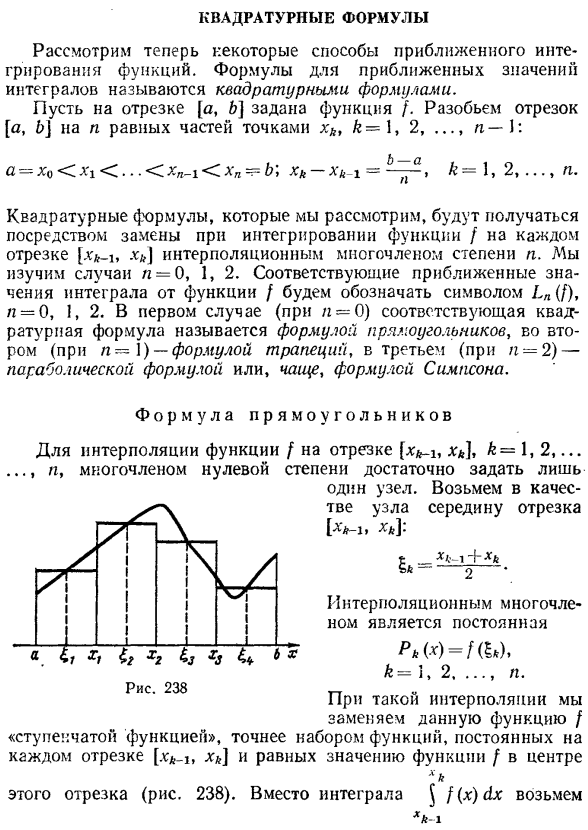
Возьмем середину узлов[xk и xk \как узел. Е ХК\ +■** Подробнее о БК Интерполяционного полинома является постоянным РВ(х) = НЫ、 к = 1,2,…н. В этой интерполяции мы заменяем эту функцию / набором «ступенчатых функций», точнее, константой в каждом сегменте[x * xk]и равной значению / центру функции от X Этот сегмент(рис. 238).Вместо интеграции ХК-1 60.4.Ортогональная формула 557. ’-1 Трапеция с соответствующей прямоугольной областью. Здесь мы опишем ортогональную формулу прямоугольника. н л гонконгских гонконгских » ыы = 2 / РК (х) ух = 2 $ 2 (60-23 к-1 х к-1 к-Я х к-1 k = I Так… Трапециевидный тип Каждый сегмент\ xk-b xk], k-1, 2,…, В n, возьмем интерполяционный полином Pk (x) в порядке 1, определяемый узлами интерполяции xk-\и xk. Г р /(х（）、1 = 0、1. Предполагая 11, см. GET ((60.20)） k = 1, 2,…н. / GY1 Вау. В Ага. Я не уверен. ВЕЛИКОБРИТАНИЯ Итак, замените эту функцию / кусочно-линейной функцией.

Вместо Интеграла-a-xg x-3 b x HK ^ /(l. рисунок 239) возьмите Интеграл xx Интеграл§Pk (x) dx, то есть замена площади кривой К. Л $ Pk (x) dx, то есть замена площади изогнутой трапеции Люкс— \ Соответствующая площадь обычной трапеции(рис. 239）、 Я * ПК (х) ух = ВК-> ВКБ-а, к = 1, 2,…н. ХК-1 Получаем квадратурную формулу трапеции это = 2 2 (бо. Двадцать четыре） к-1 к-1 Или И m = * = » + /(X1)+ Dx2)+… + Hxn]]558. Уравнение Симпсона Для каждого сегмента[xk-b x], k-1, 2 и n используйте интерполяционный полином Pk (x) 2-го порядка, определенный узлом. Интерполировать xk-x,= xk—> xk и xk затем (х-ХК^) (х-ХК） Сейчас (Х-ХК^) (Х-1;.） (1А * −1) (БК-ХК) Т (—-1 (х * * ь) Путем прямого расчета、 / ГодS L 3 (-1 * А-1 ^ −1) ((1А -■ -!）（ Ага. 1 б-в (*«(х-xkL(х-ХВ), 2.2 бы = ы * * * » = ы§ 60.Некоторые вопросы для приблизительной оценки * к-1 (•(Х-ХЙ-ТНХ-Ы, 1, Ч_1б-д 3 ( * * * * * * !）（*-＆） «» 6 ^ 1）-6″ ХК-1 И так оно и есть. Я $ ПМ ^ = ~~ [о /(^ 1-я■я / б)+1 / с]• ЛК по Теперь вы можете легко описать квадратуру Симпсона. п ХК п Вт = 2 1 ПУ (х) ух ^ б^-2 [[/（^ 1）+ | /（ы + {/Б1 * = 1 * A_X(Е = 1 60.25).

Когда вы интегрируете функцию/с каждым интервалом [xk-b xk], вы можете заменить ее интерполяционным полиномом степени N. вы получаете квадратурную формулу для рассмотрения. рассмотрим случай n= 0, 1, 2/, N ( / ), n = 0, 1, 2. In в первом случае (если n = 0) соответствующая квадратурная формула называется прямоугольной формулой, а во втором («=!«))Параболическая формула, или чаще формула Симпсона. Прямоугольное выражение Функция / интервал[x * _1, xk], k = 1, 2,… … для интерполяции в n достаточно указать только многочлены с нулевой степенью. 1 узел. Возьмем середину узлов[xk и xk \как узел. Е ХК\ +■** Подробнее о БК Интерполяционного полинома является постоянным РВ(х) = НЫ、 к = 1,2,…н. Этот сегмент(рис. 238).Вместо интеграции ХК-1 60.4.Ортогональная формула 557. ’-1 Трапеция с соответствующей прямоугольной областью.

Здесь мы опишем ортогональную формулу прямоугольника. н л гонконгских гонконгских » ыы = 2 / РК (х) ух = 2 $ 2 (60-23 к-1 х к-1 к-Я х к-1 k = I Так… Трапециевидный тип Каждый сегмент\ xk-b xk], k-1, 2,…, В n, возьмем интерполяционный полином Pk (x) в порядке 1, определяемый узлами интерполяции xk-\и xk. Г р /(х（）、1 = 0、1、…, Предполагая 11, см. GET ((60.20)） k = 1, 2,…н. / GY1 Вау. В Ага. Я не уверен. ВЕЛИКОБРИТАНИЯ Итак, замените эту функцию / кусочно-линейной функцией. Вместо Интеграла-a-xg x-3 b x HK ^ /(l. рисунок 239) возьмите Интеграл xx Интеграл§Pk (x) dx, то есть замена площади кривой К. Л $ Pk (x) dx, то есть замена площади изогнутой трапеции Люкс— \ Соответствующая площадь обычной трапеции(рис. 239）、 Я * ПК (х) ух = ВК-> ВКБ-а, к = 1, 2,…н. ХК-1 Получаем квадратурную формулу трапеции это = 2 2 (бо.

В этой интерполяции мы заменяем эту функцию f набором «ступенчатых функций», точнее, константой в каждом сегменте[x1; xk]и равной значению f центру функции от X. Людмила Фирмаль

Двадцать четыре） к-1 к-1 Или И m = * = » + /(X1)+ Dx2)+… + Hxn]]558. Уравнение Симпсона Для каждого сегмента[xk-b x*], k-1, 2 и n используйте интерполяционный полином Pk (x) 2-го порядка, определенный узлом. Интерполировать xk-x,= xk—> xk и xk затем (х-ХК^) (х-ХК） Сейчас (Х-ХК^) (Х-1;.） (1А* * −1) (БК-ХК) Т (**-**-1 (х * * ь) Путем прямого расчета、 / ГодS _L 3 (**-1 * А-1 ^ −1) ((1А -■** -!）（ Ага. 1 б-в (*«(х-xkL(х-ХВ), 2.2 бы = ы * * * » = ы§ 60.Некоторые вопросы для приблизительной оценки * к-1 (•(Х-ХЙ-ТНХ-Ы, 1, _Ч_1б-д 3 ( * * * * * * !）（**-＆*） «» 6 ^ 1）-6″ ХК-1 И так оно и есть. Я $ ПМ ^ = ~~ [о /(^ 1-я■я / б)+1 / с]• ЛК по Теперь вы можете легко описать квадратуру Симпсона. п ХК п Вт = 2 1 ПУ (х) ух ^ б^-2 [[/（^ 1）+ | /（ы + {/Б1 * = 1 * A_X(Е = 1 60.25） Или ^ [ / ] = ^ {/(А)+ /(Б)+2 [/(Х1)+ … + /（^-1）] + 4 [/（| 1）+ ..+ / (Ш-ш.

Решение уравнений.	Погрешность квадратурных формул.
Интерполяция функций.	Приближенное вычисление производных.