Оглавление:
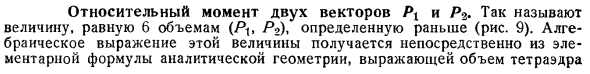


Относительный момент двух векторов Р1 и Р2
- Поэтому назовем значение, равное ранее определенному 6 объему, P2 рис.9.Алгебраическое представление этой величины получается непосредственно из основной формулы аналитической geometry. It выражает объем тетраэдра в координатной функции вершин. x1r xr как координаты точки Ax и Y, 21 как проекция вектора P на координатные оси, наконец М момент на этих осях. Аналогично, Xo, Uz, 3 показывает координаты точки B, А X B показывает проекцию на M L2. Вектор P2 моментов и моментов.
Рассуждения, которые привели к понятию, центральной оси, в рассматриваемом случае теряют смысл. Людмила Фирмаль
Затем предположим, что оси координат ортогональны и ориентируют ее так, что если она поворачивается на 90 в положительном направлении вокруг оси Ox, ось Ox преобразуется в ось Oy. Знак Том 6. Р, Р0 = U1 L 1 Х + Х У1 + г, г+ 2, 1 г г, Г2 1 Х2 4 Х2 узел 4 узел 2 4 2 4 Откройте определитель и вычтите из 2 го ряда 1 й и 4 й 3 й Том 6. Pb P2 = 11X24 L11U24 r24 1 + L12U14 2r1 Или тождество LxX1 4 Yx 4 = 0 и 3 + 4242422 4 ГГ222 = 0. Есть 6 томов.
- Четыре 4 1 4 L12 Y 4 Y 4 1 4 h 1 4 h аналитическое представление момента на любой оси. Дана ось D рис. 10, на ней выбрано положительное направление от координат O координаты x 9 y , r до координат SU , y , g. Прогнозы, Y2, 22 вектора O o представляет собой вектор P b, и величины этого момента M и N2 равны соответственно л х, г г, х х г х ч у, Х х л г, ч у у Х. Эд момент Вектор Px для заданной оси D равен Том 6. Рх, Р2 делится на ра х р х б г г м+ р 1 М1 + г р р ы Х1 + р р р х х Х1 + Р Х Х ы г х г ГХ Г Х Х У г + г г г г + г г г г р г. Из этой общей формулы мы можем получить моменты вектора Px для осей для проверки.
Далее, главный момент должен равняться нулю относительно произвольной точки. Людмила Фирмаль
Скользящие векторы, сходящиеся в одной точке. Каждый из указанных векторов можно перенести вдоль его линии действия так, чтобы все эти векторы оказались приложенными в самой точке А, как показано на рис. главный вектор отличен от нуля. Но проекция главного момента на направление главного вектора есть величина постоянная. Эти величины называются инвариантами системы векторов. когда главный вектор равен нулю. В этом случае главный момент будет одинаковым во всех точках пространства.
Смотрите также:
Предмет теоретическая механика

