Теория моментов

Теория моментов

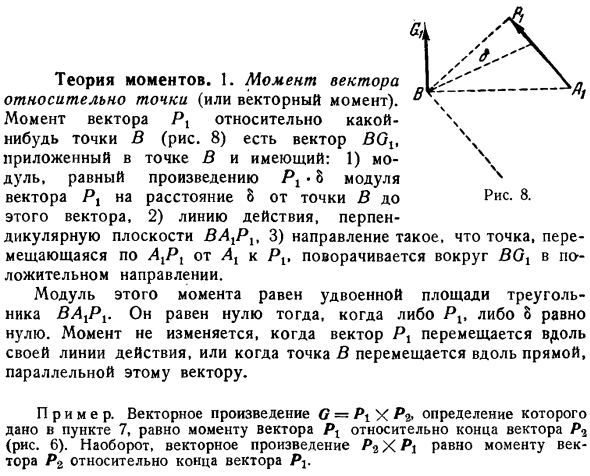
• Векторный момент или векторный момент для точки. Моментом вектора Px для точки B рис.8 является вектор BOB, приложенный к точке B, 1 расстояние от точки B модуля Px до этого вектора по модулю равно произведению Px o на o, 2 линия действия шаблона. I V характерная кривая окружности, 3 направление, в котором точка, движущаяся по кривой AX от Ax к Px, вращается в положительном направлении вокруг VOX. Модуль этого момента равен в 2 раза площади I V характеристики треугольника. Если любое из о равно нулю, то оно равно нулю. Если вектор Px движется вдоль своей линии действия, точка B движется вдоль линии, параллельной этому вектору, момент не изменяется. Образцы.

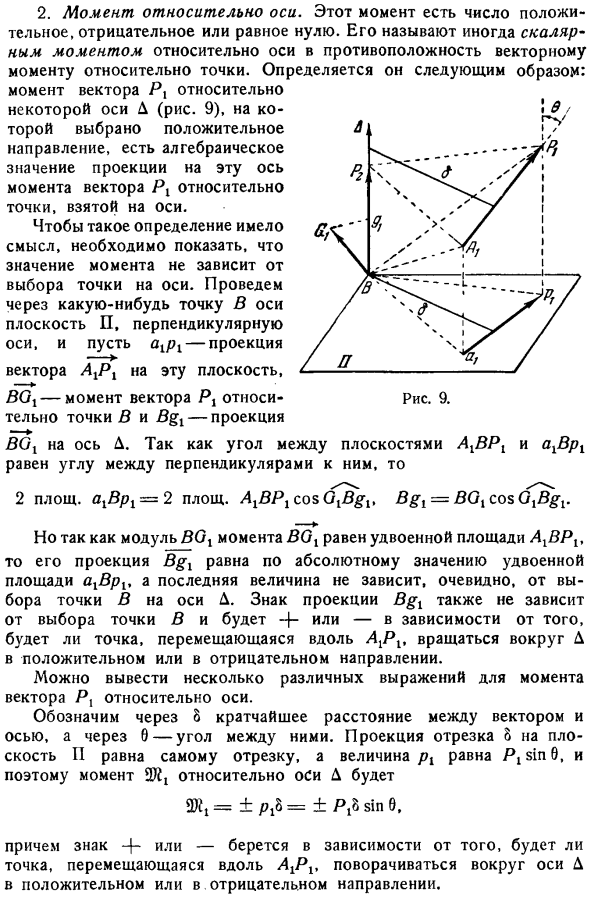
Векторное произведение C X P2, определенное в пункте 7, равно моменту вектора Px относительно ребра вектора P2 рис.6.Напротив, вектор P2 X P равен моменту вектора P2 относительно ребра вектора Pr. 2.Момент вокруг оси. Этот момент может быть положительным, отрицательным или нулевым. Это иногда называют скалярным моментом на оси, в отличие от векторного момента на оси. point. It определяется следующим образом: момент вектора Px для конкретной оси A рис.9, где выбрано положительное направление, является алгебраическим значением проекции момента вектора Px на эту ось на точку, взятую на оси.

Прежде чем приступить к механике, мы изложим теорию геометрических величин или векторов, а после этого дадим элементарные сведения из кинематики. Людмила Фирмаль

Чтобы понять такое определение, необходимо указать, что величина момента не зависит от выбора точек на оси. Нарисуйте плоскость, перпендикулярную оси через точку с осью B, axx проекция вектора AXX на эту плоскость, бокс момент вектора Px относительно точки B, B x проекция B6x на оси D. Поскольку угол между плоскостями AgBX и a1Bp1 равен углу между их перпендикулярами 2 квадратных ahBrh = 2 квадратных. AXBX cox OXB X, B x = BOX cox CXB X Однако, поскольку модуль BCX момента B6X равен 2 кратному модулю площади AXBR, то его проекция B x равна 2 кратному модулю площади axBx по абсолютному значению, и величина последнего, очевидно, не зависит от выбора точки B на оси D.

• Знак проекции B x также не зависит от выбора точки B, точка, которая движется вдоль AXX, будет+или, в зависимости от того, вращается ли точка вокруг D в положительном или отрицательном направлении. Для моментов вектора Px для оси можно вывести несколько различных выражений. Кратчайшее расстояние между вектором и осью обозначается O, а угол между ними равен 0.Проекция отрезка o на плоскость II равна самому отрезку, а величина px равна P nO, поэтому момент на оси D 9 = п = п 81P о Кроме того, знак+или используется в зависимости от того, вращается ли точка, движущаяся вдоль оси AXX, вокруг оси D в положительном или отрицательном направлении direction.

Он помещает отрезок BP длины P2 в положительном направлении на оси A и показывает объем тетраэдра, который имеет AXPX и BP2 в качестве противоположных концов, через объем Px, P2. кроме того, он принимается как положительный или отрицательный, в зависимости от того, вращается ли точка, движущаяся от одной начальной точки к конечной точке вектора Px или P2, вокруг другого вектора в положительном или отрицательном направлении.

Необходимо, однако, заметить, что механика не раскрывает действительных причин физических явлений и довольствуется заменой их некоторыми абстрактными причинами, называемыми силами и способными вызвать тот же механический эффект. Людмила Фирмаль

Тогда вектор px момент для D будет равен: На самом деле это уравнение верно по знаку и абсолютной величине, потому что если вершины A1 и Px переместить в положение ax, то рассматриваемый объем не изменится, а объем V приведет к новому тетраэдру, равному площади a1Bp1 по произведению P2 3 min 1.Таким образом, абсолютное значение момента, равное 2 кратной площади ахбрх. Равно значению, деленному на 61 P2.

Смотрите также:

Предмет теоретическая механика

Векторное произведение двух векторов	Аналитические выражения моментов вектора относительно осей координат
Скользящие векторы. Пять координат скользящего вектора	Пять координат скользящего вектора