Оглавление:






Вынужденные колебания системы с двумя степенями свободы под действием синусоидальных возмущающих сил
- Когда возмущающая сила действует на систему в течение всего процесса колебаний, возникают сложные колебания. Это результат наложенных друг на друга вынужденных и свободных колебаний системы. Дифференциальные уравнения движения системы могут быть составлены с использованием уравнения Лагранжа. Где обобщенные координаты системы T-кинетическая энергия системы, P-потенциальная энергия, а Q — сила возмущения. Если система имеет 2 степени свободы, то 1, 2.
В случае 2 степеней свободы, подставляя Т и П в уравнение 1, получаем систему дифференциальных уравнений АП 1 АИ з cu9i c1rCh1 СШ грех Д 6 УФИ ам Ы cn9i с Qa HG sin pt 6 2 Где сила возмущения Q 0 считается изменяющейся по закону синусоидальных волн в часто встречающихся случаях предельное рассмотрение имеет существенное практическое значение Ци 0 беспроводной грех ПТ 6, СМО м грех ПТ 6. 3 Общее решение системы дифференциальных уравнений 2 состоит из общего решения однородной системы уравнений и частного решения неоднородной системы.
Кривошип, вращающийся с постоянной угловой скоростью ш, считать тонким однородным стержнем, а камень А — точечной массой. Людмила Фирмаль
Общее решение однородного Система представляет собой ранее рассмотренную свободную вибрацию и обнаруживается в соответствии с методом, описанным в b настоящей главы. Поэтому мы сосредоточимся на определении конкретного решения этой системы, которое представляет собой вынужденную вибрацию системы. Найдите конкретное решение в следующем формате. П грех п 6, Pn81n р с. 4 Вводя эти значения в уравнение 2, мы попадаем в систему алгебраических уравнений. c1i-P4i ОИ ти-П является ОА ТФИ. Один Си АИ Р1 Си-Р ИИ Р1-я, 1 Неизвестный Db D Детерминанты этой системы исчезли Си-Р ас ы — Си-рай 2 0, 6 При резонансе, если p kg или p Aa.
В этом случае конкретное решение системы не найдено в виде 4. Дифференциальные уравнения движения системы также могут быть построены с использованием теоремы общей динамики. Для решения задачи определения вынужденной вибрации рекомендуется следующая последовательность действий Первый метод заключается в использовании уравнения Лагранжа. 1 Выбрать обобщенные координаты и настроить выражение кинетической энергии системы. 2 найти представление потенциальной энергии или вычислить обобщенную силу. 3 составить дифференциальное уравнение движения системы и ввести значение кинетической энергии и потенциальной энергии или обобщенной силы в уравнение Лагранжа.
Ищем конкретное решение дифференциального уравнения движения системы, находим амплитуду обобщенных координат. б в выражении амплитуды, равном знаменателю нулю, находим частоту возмущающей силы, при которой возникает резонанс. Второй метод заключается в применении общей теоремы динамики. После выбора обобщенных координат система непосредственно строит дифференциальные уравнения движения на основе выбранной теоремы динамики. Дальнейший ход решения такой же, как и в первом способе. Задача 18.24.С помощью измерительного прибора блоки массы М могут перемещаться по абсолютно гладкой горизонтальной плоскости surfaces.
Конец однородного стержня массой M длиной OA 1, коэффициент жесткости которого соединен с пружиной, равной c. Другой конец закреплен с помощью шарнира. Центр тяжести стержня находится на расстоянии OS a от шарнира. Определить вынужденные колебания блока, когда горизонтальная сила действует на блок Р Фосин ш значение вибрации в блок По вопросу 18.24. Решение. Система имеет 2 степени свободы.
- Его положение можно определить по 2 координатам угол поворота стержня, подлежащего отсчету от вертикали. Координата X блока, подлежащая отсчету от положения равновесия блока до вертикального положения стержня понятно, что пружина не деформируется. На блок действуют силы реакции и возмущения пружины. Дифференциальное уравнение линейного движения блока имеет вид рисунок а mH — c x-I-q F0sin tot, 1 Где x — f — удлинение пружины при малом склонении rod. To отредактируйте дифференциальное уравнение вращения стержня рисунок Б, момент силы тяжести на горизонтальной оси, проходящей через точку О Mga sin I -АФГ-АФ. Момент реакции пружины на ту же ось КЗ, потому что Ф Х ф З.
Здесь, на небольшой угол поворота, принято использовать сов Е1.Тогда дифференциальное уравнение колебаний малого стержня выглядит следующим образом Itp — Mgatp c x — 2 Перепишите дифференциальные уравнения 1 и 2 в виде МХ СХ-с ф КТ грех т, я м Мга хп Ф-сlx 0. Общее решение системы состоит из общего решения однородной системы уравнений и частного решения неоднородной системы. В зависимости от условий необходимо определить вынужденную вибрацию блока, так чтобы искалось только конкретное решение неоднородной системы, определяющее искомую вибрацию. Мы ищем частное решение, устанавливая сравни ФЛ грех со х 4. 4 И затем… Х — leosin со, Ф — такие офисы не имеют sinco.
Зависимость между скоростью центра инерции и скоростями точек материальной системы имеет вид Заметим, что положение по отношению к точкам т. Людмила Фирмаль
Подставляя значения этих переменных и их производных второго порядка в систему 3 и уменьшая их в sinw , находим систему алгебраических уравнений, определяющих A и B. с-та А-класс B ч Мы определим его отсюда И.-с I Ио СР Мга-З 2 А 1 С — М о — ХЛ — ХЛ с afga-Зо 6 То есть амплитуда вынужденного колебания блока. Вклад этого значения И в первом из уравнений 4 находим вынужденную вибрацию блока Потоком Мга-Ж х млва— КЗ выбрано исключительно для удобства визуального mAigaJco cAfga Вт Координата x, определяющая вибрацию блока, бесконечно возрастает, когда заканчивается правый знаменатель последнего уравнения.
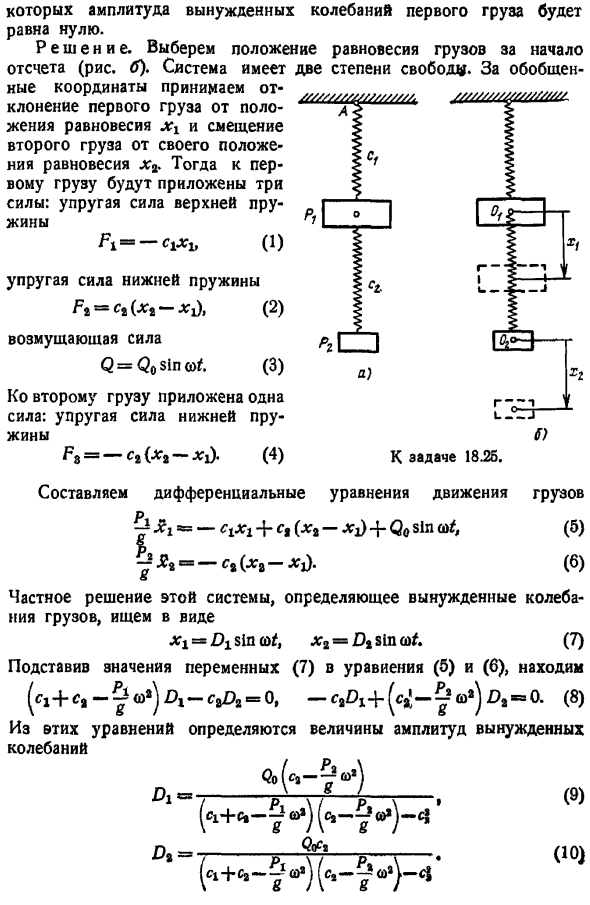
Здесь используйте следующие значения, чтобы найти значение резонанса. cl МСР ммга г с МКП mMgaf — 4cmMlga 8 Из 4 значений с 2 отрицательными значениями нет ни одного sense. So, согласно 8, имеет 2 резонансных значения. Задание 18.25.ПВ нагрузки рисунок подвешен к неподвижной точке с помощью пружины коэффициент жесткости СХ. Вертикальная сила заклинивания Q Q0slnco приложена к нагрузке Px. Нагрузка Pj, амортизатор колебаний, подвешена к нагрузке Px пружиной коэффициента жесткости ct. Определите массу коэффициента жесткости с и 2-й нагрузки Р, игнорируя массу пружины. Амплитуда вынужденного колебания первой нагрузки будет равна нулю. Решение.
Выберите положение равновесия товара в начале координат рисунок B .Система имеет 2 степени свободы. Обобщенный Получаем различные координаты как отклонения первой нагрузки от положения равновесия xx, так и смещения второй нагрузки от положения равновесия xa. Затем к первой нагрузке прилагаются 3 силы сила упругости пружины в верхней части А —С1 Б 1 Сила пружины П с Х4-Х1, 2 Сжимать силу Вопрос Qosin в 3 1-я сила приложена к 2-ой нагрузке. Сила упругости нижней пружины. ФС — ч а — 1 — 4 По вопросу 18.25.
Дифференцировать уравнение движения Л — с ХЗ Х1 Qо слу — — Груз 8 6 Конкретное решение этой системы, определяющей вынужденную вибрацию груза, требуется в следующем виде Х1 D1slncoi, ХД Dtsln0 Ф. 7 Если присвоить значение переменной 7 выражениям 5 и 6 Эти уравнения определяют амплитуду вынужденного колебания Ди Р. 9 Согласно формуле 9, если выбрать коэффициент жесткости 2-й пружины Ci и массу Pt, то амплитуда вынужденного колебания 1-й нагрузки исчезает. с jv. 0. Он Поэтому при заданной частоте возмущающего усилия w всегда можно выбрать коэффициент жесткости дополнительной пружины и массу 2-го груза для поглощения вынужденного колебания 1-го load.
В этом случае необходимо обратить внимание на резонанс, возникающий при исчезновении знаменателей 9 и 10. с, е — -б — — р 0. 12 Величина определяемой угловой скорости. Серверы имен равенства 11, 9 и 10 не удовлетворяют 12, потому что они не исчезают. Однако не всегда удается сохранить точно такое же значение w.
Смотрите также:
Предмет теоретическая механика

