Оглавление:














Политропные процессы.
- Политропный процесс До сих пор этот процесс считался очень четким признаком.Изобарный-при постоянном давлении.Изотермическая-постоянная температура; адиабатическая-когда отсутствует теплообмен между рабочей жидкостью и внешней средой.
environment.In в дополнение к этим процессам вы также можете представить себе множество процессов с другими постоянными функциями. Чтобы назвать технологическую линию политропным процессом, мы договорились о процессе получения идеального газа с постоянной теплоемкостью-политропа. Из определения политропного процесса видно, что основные термодинамические
Чтобы назвать технологическую линию политропным Людмила Фирмаль
процессы-изотермические, изобарные, изотермические, адиабатические-являются частными случаями политропного процесса, когда они протекают с определенной теплоемкостью. 。 Теплоемкость политропного процесса Cn составляет от+ sy — Да.
Количество тепла, содержащегося в политропном процессе, может быть выражено как произведение удельной теплоты процесса cn, обусловленной разностью температур t2, в конечном состоянии и в исходном состоянии. < 7 * = СП(Т9-tJudq ^ КСПД.(7-19) Уравнения политропного процесса выведены на основе уравнений первого закона термодинамики. DQ = cndT = CpdT-vdp и dq = c ^ dT = cvdT + pdu. 。Из этого уравнения、 (СП-СР)/(СП-СV)=• — ВДП / ПДВ. Уравнения
- политропного процесса выведены на основе уравнений первого закона термодинамики. ЙД = КСПД = cpdt аппликации-ВДП и DQ = с ^ ц = с ^ Т + БРП. 。Из этого уравнения、 (СП-СР)/(СП-СV)=• — ВДП / ПДВ. Если обозначить уравнение левой части * уравнения через n, то получим (c * — cp)/(cn-cv)= n и N dv / v = — dp / P. Если мы интегрируем полученное соотношение от начала до конца процесса、 Н v2lvx ЛГ = ЛГ pjp2 Или ПВН = сопи (7-20) Полученное уравнение является уравнением политического процесса. • Политропный показатель N принимает определенное число для каждого процесса.Основные процессы:
изосум n =±oo, изобарный n = 0, изотермический n-1 и теплоизоляция n-K. Поскольку уравнение политропа отличается только величиной адиабатического уравнения и показателем Пу, очевидно, с помощью уравнения, аналогичного адиабатическому процессу. Н-1 = J Т ^ Я / / / ^ 22/7 \ =(Р2 / Рl) Н. Теплоемкость политропного процесса определяется из уравнения n =(cn-cp) 1 (cn-c0), из которого cn = cv [(n-
что все соотношения между основными параметрами могут быть выражены Людмила Фирмаль
k)/(n-1) 1. (7-21) Уравнение (7-21) позволяет определить теплоемкость политропного процесса для каждого значения p. Подставляя значение n в частный случай формулы(7-21), получаем удельную теплоту рассматриваемого процесса. cn =±oo; процесс изоляции n = k, cn-0. Уравнение работы изменения объема, осуществляемого корпусом при политропном процессе, имеет такой же вид, как и уравнение работы
процесса теплоизоляции. / = 11 /(Н-1)1 (ЛП-п * У2),. (7-22) Или Н-1 / = [RTJn-1](1-m2 / m)= IpM — * 01 и -.(Pjpi)Н] =-[ПЛ / {П-1)] [(1-м ^- ‘ б(7-23) Изменение внутренней энергии газа и теплоты в политропном процессе определяется следующим уравнением: ДМ = СV(Т2 -/,);. ‘Д-СN (Т2-ТХ = л (п-к)!) (N-1)1(/ 2-/、)。(7-24) Как с процессом изоляции, внешняя работа доступная в политропном процессе、 / / ‘=-^ ВДП= [«/(»-1)] = 1)1 дл-Д;). (7-25) Изменение энтальпии в политропном
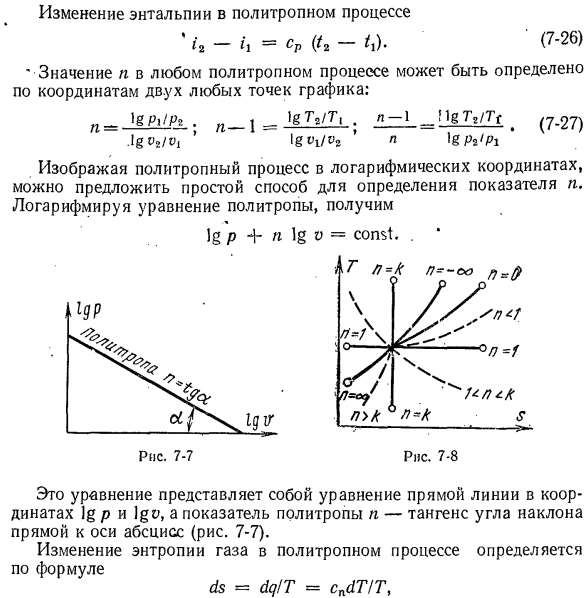
процессе ‘- ч./(= — У.) (7-26) «Значение n в политропном процессе можно определить по координатам 2 точек на графике. игпи / Пт п! _ lgTVT, n-1 ^ HgTwTf ^(7_27) .lgv2 / Ви ‘IgvjVz 9 Н \ ГПИ’ Пи Рисуя политропный процесс в логарифмических координатах, мы можем обеспечить простой способ определения показателя P. логарифмическое политропное уравнение、 Это уравнение является линейным уравнением в координатах log p и Igy, а политропный
показатель P является касательной угла наклона прямой к оси абсцисс (рис.7-7). Изменение энтропии газа в политропном процессе определяется уравнением ДС = йд / Т = КСПД / Т、 Или для окончательного изменения статуса С2-с-в 7 классы 7 \ = Ф-jEiy] ЛН Tm1Tr. (7-28) Политропный процесс представлен специфической кривой на диаграмме РС (рис.7-8), расположение которой зависит от индекса р. Рисунок 7-9 показывает расположение политропного
процесса на диаграмме pv, которая появляется из той же точки, в зависимости от размера индекса p. Рассмотрим, как изменяется внутренняя энергия газа в многограннике. нный процесс. в изотермическом процессе при N = 1, внутренняя энергия газа не изменяется(У2 = уй). процесс изобарного расширения, где r = 0, увеличивает внутреннюю энергию. в изоволюмическом процессе с
подводом тепла n =-oo внутренняя энергия увеличивается.Отсюда, в случае n <1, все политропные процессы, т. е. процесс расширения выше изотермы и процесс сжатия n> 1, протекают с увеличением внутренней энергии газа.Политропный процесс, т. е. процесс расширения n> 1 ниже изотермы и процесс сжатия n <1, происходит с уменьшением внутренней энергии газа. Рассмотрим, как изменяется знак теплоты при политропном процессе (рис. 7-9). в процессе
термоизоляции тепло не подается и не расходуется. removed.In изотермический (n = 1), процесс расширения изобарного (n = 0) и изотермического (n =-oo) питания heat.As в результате все политропные процессы, т. е. процесс расширения над изоляцией в k> n> — oo и процесс сжатия в момент oo> n> k, продолжаются с подачей тепла в рабочую жидкость. Oo: политропный процесс расширения в> n>и-OO 0tdT> 0 и du <0, dT <0).И из Формулы удельной теплоты= dq / dT
мы видим, что она действительно negative.In на практике это означает, что при подаче тепла в эти процессы температура снижается, а при удалении тепла температура снижается. Н = + 00 н = д Расширение Рисунок 7-9 Н-1 В Хака. Глава 7 тестовые вопросы и примеры 1.Определите основные термодинамические процессы. 2.Как контурные линии, изострены,изотермы и теплоизоляция показаны на
диаграмме ry? ^ 3.Опишите уравнение основного процесса. 4.Описывает формулу для связи между параметрами P, v и T каждого процесса. 5.It объясняет повышение температуры при расширении газа в изобарном процессе. 6.Докажите, что теплбга равна изменению энтальпии в изобарном процессе. 7.Опишите формулу работы по изменению количества газа в каждом процессе. 。 8.Опишите формулу одноразовой (полезной) работы для каждого процесса. 9.Почему температура повышается во время сжатия, когда температура
падает во время адиабатического процесса расширения тела? 10.Каково относительное положение Изотерм и теплоизоляции на диаграмме ввода-вывода, построенной из 1 точки между расширением и сжатием газа? 11.Что такое процесс, называемый политропным? * 12.При каких условиях происходит основной процесс получения идеального газа?Политропы? ■* 13.Напишите уравнение политропа, чтобы показать, насколько сильно изменяется индекс политропа. 14.Какова величина политропного показателя в основном процессе? 15.Напишите уравнение теплоемкости для политропного
процесса и укажите, что теплоемкость получается из этого уравнения для всех основных термодинамических процессов. 16.In в каком процессе уменьшается внутренняя энергия и в какой энергии она увеличивается?Докажите это в богатой диаграмме. 17. «Какой политропный процесс обеспечит газ теплом и в каком процессе тепло будет удалено?’ 。 。 18.In какой политропный процесс, почему теплоемкость становится отрицательной?Что это значит? 19.Какие уравнения используются для расчета изменения энтропии
процесса изотропизма, изобарного, изотермического, адиабатического и политропного? Пример 7-1 баллон 0,12 Л * 3 содержит абсолютное давление 10-155 Н / м2 и температуру’50°C воздуха.Определить изменение конечного давления, теплоты и энтропии при повышении температуры воздуха до 150°С. Масса воздуха в цилиндре м =-^ р—10-ть, 12 [29 Кси ‘ А7 \ 287.04-323. Конечное
давление Р2 = Дж ^ = И2 ^ = 13) м(Вт Конечное давление Количество подаваемого тепла Q = t (cvm fc(2-coin tt)= 1.29(0.722.150-0.718-50)= 94.0 кДж、 М = м(У2-уй.= 1.29(108.5-35.9)= 94.0 кДж.Изменение энтропии С. з-Си-MCV в TJTX = 1.29-0.72.2.3 ИГ 423/323 = 0.252 kJI (кг град) Пример 7-2 при постоянном абсолютном давлении 2 бар и температуре 288°к 2 кг воздуха расширяется до конечной температуры 423°к. это будет определять конечный объем воздуха, количество подаваемого тепла и работу расширения. Ответ: V2 = 2,54
м3; Qp = 277 кДж; L = 79,2 кДж. Пример 7-3 абсолютное давление 6 бар, температура 300°К, 12 кг воздуха расширяется при постоянной температуре, увеличиваясь в объеме в 4 раза.Определите начальные и конечные параметры воздуха, количество подаваемого тепла и работу расширения. Начальное количество воздуха определяется из уравнения состояния. г ^ — 287.04-300 г 1.725 1 ФЛ 6.10 » Конечный
объем. • П2 = 1.725-4 = 6,9 х 8 / Окончательное давление равно п, УГ 6-1. 725, с- Работа расширения L ‘= plVl в V2 / V1 = 2,303-6.105 ‘1,725 Ig 6.9 / 1,725 =’ = 14500000 j,= 1450 kJ. Количество подаваемого тепла равно работе расширения: Q-L = 1450 кДж.Пример 7-4. Дает 2 кг [Ttri начальное абсолютное давление 10 бар и температуру 600°[K расширяется адиабатно до конечного давления 1 бар.Определите конечный объем, конечную температуру, работу расширения.Адиабатический индекс двухатомного газа * Начальный
объем воздуха определяется из уравнения состояния. .у MgTj ^ 2.287.04.600 = М 1 пл 10.10 с Из уравнения адиабаты = VMlp2yk = 0,345 (10/1)» / i-1,79 м Конечная температура определяется по формуле Т _ Р2 У2 = MO5 ‘ 1.79 2 мистер 2-287. Ноль четыре Расширение работы равна L = | 1 /(A-1)1(RL-p2U2)= [10 / /(1.4–1)](10-0.345-1.1.79)= 415000 j = 415 кДж. Пример 7-5.Начальные параметры px 1 бар и 7 \ 300°К 3 кг воздуха сжимаются вдоль политроп до p2 = 15 бар и G3 =
500°К. Определите политропный индекс, конечный объем, работу сжатия и количество отводимого тепла. Скорость политропа (П-1)/-^ 16,500 / 300 ^ IgPz / РХ ИГ 15/1 1.23 отсюда.Конечный объем y,= 3.287.04.500 2 87 / <3 Р2 15.10 ‘ Первоначальный объем Ви = П2(РМ1 / п = 0.287 (15/1)!П.23= 2,57 м*.Определение и сжатие работы: Л = [1 /(л-1)1-p2K2)= 110 в(1.23-1)(1•2.57- -15•0,287)= 763000 Дж = 763 кДж.Количество отводимого тепла М = / понятно ^ л(п-/ р)/(н-1) 1(Т2-7)=-3. 0.72 1(1.23-
1.4)/(1.23-1)1(500-300)= -316 * 3”、 Куда? цв = КС ^ с = 20.8 / 28.9 = 0.72 кДж /(кг * град).Изменения внутренней энергии И»= / yas » (G2-7 \)= 3•0.72•200 = 432 Кю. % Если индекс сжимает воздух с l = 1.23, то работа сжатия делится на 2 части.Остальные части расходуются на увеличение внутренней энергии рабочего тела. В Примере 7-6 политропного процесса температура воздуха падает от 120 до 50°С. начальное атмосферное давление rg составляет 5 бар.Определите
изменение энтропии воздуха, если в рассматриваемом процессе воздух подается с теплотой 60 кДж.Теплоемкость воздуха (см. Пример 7-5) С0= 0,72 кДж / (кг * град).Определите показатель политропа из уравнения д = ЧВ (п-к)!(Н-1) 1 (Т2-/、)、 Откуда (п-1.4)/(Н-1)=.м / ЧВ (ТТ-
ТТ)= 60 / 0.72(50-120)= -1.19、а• ‘ н = 1.18. определите p2. pppi =(WJ-zc-n, pa =((где / ^ — n^ ‘= 5(323/393)6•50 = J, 38 бар. Найдите изменение энтропии. s2-st = cp в 7Y7 \ — R в pjpx = 1.0•2.3 log 0.822—0.287 * 2.3 log 0.276 = 0.13 кДж / (кг * град). Изменение энтропии также можно найти в другой формуле: S2 — = InT2fTx = 0,173 кДж / (кг-град).
Смотрите также:
Решение задач по термодинамике
| Изохорный процесс. | Основные положения второго закона термодинамики. |
| Изотермный процесс. | Круговые термодинамические процессы, или циклы. |

