Оглавление:





Вычисление секториальных характеристик
- «Расчет характеристик сектора. Время расчета Секторные характеристики поперечного сечения, т. е. величина. Jxwddy, Jjrtodds, J и Е> * ДДС, Для прямоугольного профиля, Интеграл должен быть вычислен из произведения двух функций в виде J и ф (г)Ф ©ДС. Если
хотя бы одна из функций линейна, вы можете найти этот Интеграл, используя простую графоаналитическую технику ниже. Создайте график или график функций f(y)и f (y). 198).
Найти площадь Q участка F (y) и умножить абсциссу F0 линейного участка, Людмила Фирмаль
соответствующую абсциссе центроида участка F.: J и ф(г)ф (г)6ds=0. Теперь давайте посчитаем Jw. Применяя правила графоаналитического обнаружения интегралов, получаем:, O (G1a2(b-t) h, 1st, 2IG] „ , ^ — ^ — 3 —— — + 2 — г з Т-Т Дж д»+ 11-й h2t ч, ) * 2 ‘2 • 2’ 3 ‘2 °’ п Рис, 200. Все расчеты должны быть сделаны немедленно в цифрах. Г) З е т о В О Е С Е Ч Е Н И Е. выбрать опорную точку для центра
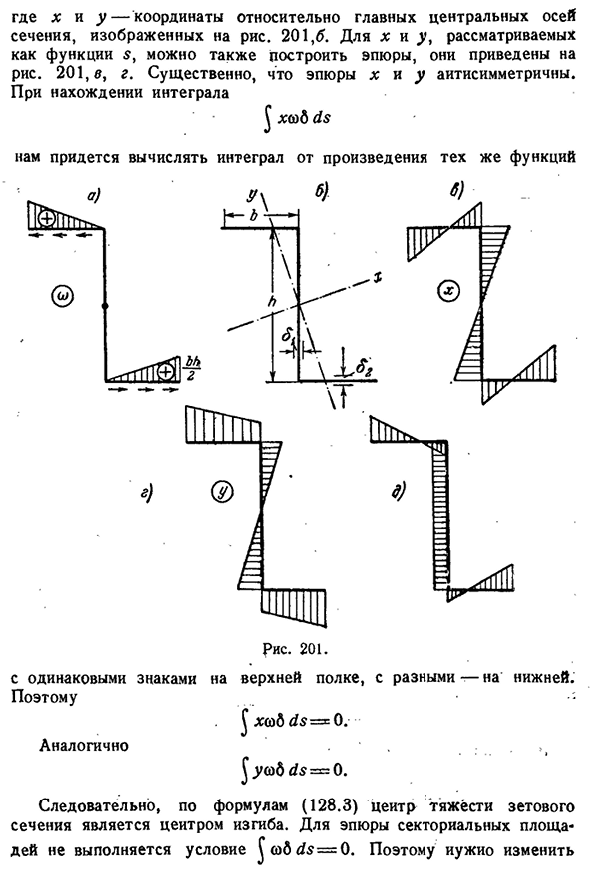
тяжести вспомогательной штанги и секторной области на пересечении Рыс. 201, а.Интеграл Стены и полки. Для нахождения центра изгиба нам необходимо вычислить J-ds, J ua>6ds,§ 132] расчет секторных характеристик 291 Где X и y-координаты главной центральной оси сечения, показанного на рисунке. Для возможных
- функций X и y в 201.5 S можно также создать график. 201, в, G. It существенно, что сюжеты x и y антисоциальны. Когда вы хотите Интеграл \ xcoS ДС Необходимо вычислить Интеграл произведения одной и той же функции На верхней полке те же знаки, а на нижней—разные. Итак — ^XG>Sds==0. Кроме того, д Я б ы-В. Итак, согласно
формуле (128.3), центром тяжести z-сечения является Центр изгиба. Условие fo>s d s=0 не выполняется на графике области сектора. Так что вам нужно измениться 10 * 292 изгибное кручение тонкостенного стержня[глава XI Начало отсчета площади сектора. J (o) — c) добавьте константу C в секторную область, как есть 6d s=Q, и (s) добавьте константу C Или Bgk6g-с [2М, 4- / ц и J = О.
И так оно и есть. с-2&6.4-л6/ На рисунке показана эпюра основной разделительной области (co—d). 201, д. д.) т р у Б А С Р А З Р Е З О М(рис. 202). Выбрав Людмила Фирмаль
вспомогательный полюс в центре и цачало опорный сектор области при F=0, получим: (s=f/? ’, х=7?с COS<р, й»=.Rsinq), JX у=НРя). Вычислите интегралы, содержащиеся в первой формуле(128.3): Два. Джей йоу>БС Д С=С/? 4У<Р СПФ< / Ф= — 2ly/?. o формула (128.3)*r-2^R * _op x C-n R4~перемещает полюс к центру изгиба. По формуле (128.2) = f√ * 27?г=/?’(f-| — f 2 секунды). Он выбирает начальную точку области сектора、 \д ДС=0. Очевидно, что это условие выполняется, если мы заменим начальную точку на середину дуги, то есть угол f, который изменяется от-l до -| — l. ®=ε(f+2 sin f). Теперь рассчитаем момент инерции: +» ДМ=] ДС=р л т>(ф-| — 2z1p ф)’< / ф= — я=/√5BL(л-6)=5=8, 11ya5b.
Смотрите также:
| Закон секториальных площадей | Стержень, нагруженный бимоментом |
| Уравнение стесненного кручения | Некоторые примеры стесненного кручения |

