Оглавление:



Общие теоремы о моментах
- Общая теорема момента. Рассмотрим некоторые основные и очевидные свойства статических моментов и моментов инерции. Чтобы перечислить эти свойства, просто используйте слово «момент», если вы говорите о свойствах, общих для всех моментов. В противном случае, вы увидите суть проблемы. Т Е О Р Е М А1.
Момент составной площади равен сумме моментов ее частей. Фактически, если фигура состоит из двух частей I и II, то Интеграл$P (x, y) d F — $P(x, y) d F+J P (x, y) по свойству dF. Ф Ф, ФН Но J P (x, y)D F-это момент всей области. Ф
Части — это части I и II, времена одного и того же названия., J-L+LH S l e d s t V I e. Людмила Фирмаль
при вычислении момента области, ограниченной двумя замкнутыми контурами (двумя связями), вычислите момент области, ограниченной внешним контуром и окруженной внутренним контуром). Действительно, момент Y-это область, заключенная
в контур G, момент области, ограниченной кривой G, равный сумме перед JN, и момент затененной части J: L-a i4″J’.§ 96] общая теорема о моменте 209 И так оно и есть. Y-Y[Jlv это замечание часто используется при расчете момента инерции. Т Е О Р Е М А2. Осевой
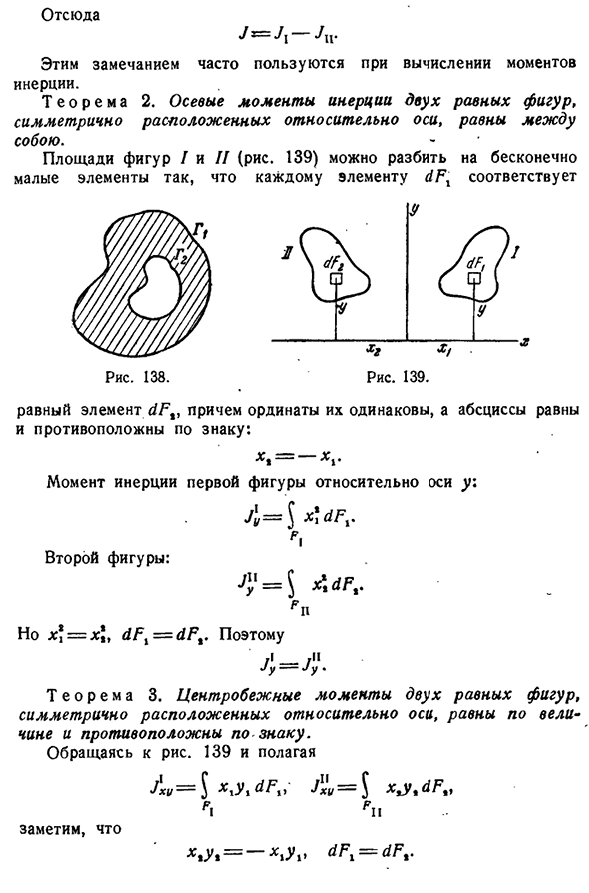
- момент инерции двух равных фигур, расположенных симметрично относительно оси, равны друг другу. Участки фиг I и II(рис. 139) могут быть разделены на бесконечно малые элементы так, что каждый элемент dFt соответствует равный элемент ДПФ, координаты которого совпадают и абсцисса которого противоположна знаку: икс=, — Момент инерции первой фигуры относительно оси Y. Дя-\х \ Д Ф в Вторая фигура: J ’ 1=J Ф Я Но xj=xj, dFx=dFt.
Итак, Джи-Джи. Т Е О Р Е М А3. Центробежный момент двух равных чисел, расположенных симметрично относительно оси, равен величине знака и противоположен. Обратимся к рис. 139X (/=X1U1dFv УБ{/=5х, у Т промышленности организует в интернет Ф Н Берегись этого. х т т= — х J в ДФ=тфп.210 теория момента инерции[Глава VIII И так оно и есть. Семь. — — Jxy-Jxy
Если одна из осей является осью симметрии, то центробежный момент инерции равен нулю. Например, ось симметрии — это ось Y. Людмила Фирмаль
Он делит фигуру на две равные части I и N, расположенные симметрично относительно этой оси. -О первой теореме J х г=J х г-ИК Дж lxy • В результате Третьей теоремы 71—7Н И так оно и есть., Лу=0. Ось, для которой центробежный момент равен нулю, называется главной осью инерции. Мы установили, что симметрия фигуры относительно одной из осей является достаточным условием того, что ось является главной. Но это условие не обязательно.
Смотрите также:

