Оглавление:
















Кеплерово движение (движение под действием центральной силы)
- Две точки массы взаимно притягиваются модулем с силой 1. Где i и m-первая масса и 2-я точка-это константа всемирного тяготения, где r-расстояние между точками. Формула i представляет закон всемирного тяготения, открытый Исааком Ньютоном. Этот закон иногда называют закон Ньютона. Формула 1 сохраняет свою простую форму, когда тела притягиваются друг к другу, а не к материальным точкам. Если тело представляет собой сферическую структуру, то каждое тело имеет следующие формы Шар и плотность одинаковы во всех точках тела на одинаковом расстоянии от одного и того же center.
В этом случае ставится задача изучения движения центра инерции 2-х объектов Действие взаимного притяжения ничем не отличается от изучения 2-х точек движения, которые притягиваются друг к другу по закону Ньютона. Эта задача называется классической задачей тела 2. Его геометрическое решение является первым i. Оно было дано Ньютоном. После этого аналитическое решение было предоставлено Даниэлем Бернулли. Леонард Эйлер подробно изучил эту проблему.
Таким образом, картина движения существенно отличается от рас-смотренной в предыдущей задаче — при данных начальных условиях движения груз асимптотически приближается к положению статического равновесия, ни разу не переходя через него. Людмила Фирмаль
Сила мира Притяжение 1-это консервативная сила. Силовая функция этого силового поля u определяется уравнениями cfl ln1 и n2. Поместите znt l в уравнение 2 и получите функцию y y. Ньютон potential. In эта формула, индекс массы является omitted. In в научной литературе указанные названия всегда применяются к Формуле 3, хотя этого придерживается Точнее, мы называем ее ньютоновской силовой функцией. 2 3 Если объект не имеет сферической структуры, то потенциальное притяжение всего объекта задается следующей формулой g1-расстояние от частицы dm до точки притяжения единицы массы. Интеграл рассчитывается по всей массе тела.
Если рассматривать Землю как объект сферической структуры, то ее ньютоновский потенциал равен j0 e f l 5, где l m-гравитационный параметр, равный произведению постоянной всемирного тяготения на массу Земли, а r-расстояние от центра Земли до точки притяжения. Численно p 3, 98-106 км гравитация Земли равна r-r, t-масса притягиваемой точки, g-радиус-вектор притягиваемой точки, проведенный от центра earth. In При изучении движения космического аппарата вблизи Земли последний рассматривается в первом приближении как структура сферы, а космический аппарат-как материал point.
Масса Земли, af, неизмеримо больше массы космического аппарата, и в результате мы можем игнорировать влияние массы, m, на массу. Проблема движения космического аппарата в этом случай является частным случаем классической проблемы 2 тела. Траектория движения космического аппарата под действием силы тяжести Земли задается формулой где r-радиус-вектор Проведенное от центра Земли к космическому аппарату, e-эксцентриситет, p-фокальный параметр конической части, а cp-угол между осью полюса и радиус-вектором r. Это уравнение В зависимости от величины эксцентриситета эллипс в e1, Парабола в e1 и коническое сечение в e1 определяют гиперболу. Величина e зависит от начальных условий movement.
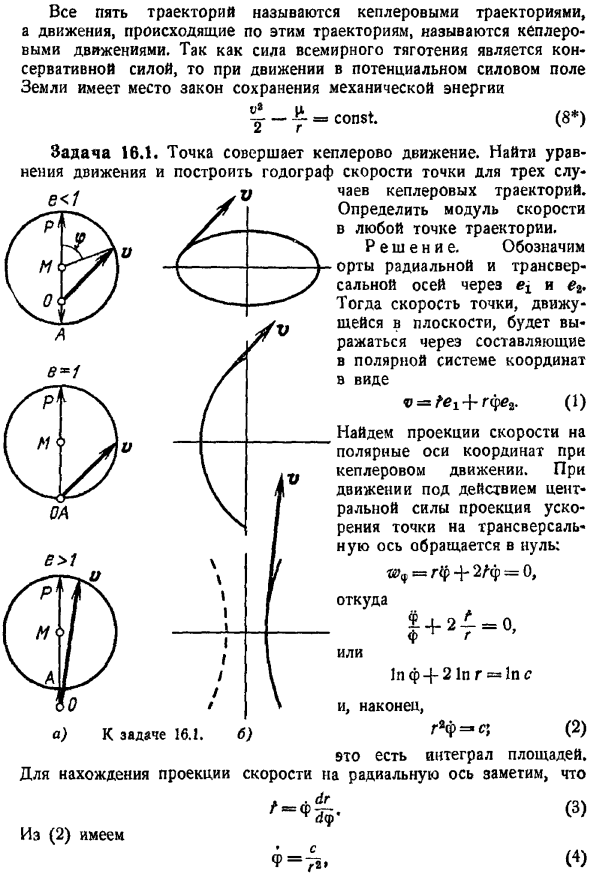
Кроме указанного случая, траектория может быть линейной и Круговой в радиальном направлении при определенных начальных условиях. Все 5 проходов называются Кеплеровскими. Траектории и движения, которые происходят вдоль этих траекторий, называются кеплеровскими движениями. Так как сила всемирного тяготения является консервативной силой. Потенциальное силовое поле Земли содержит закон сохранения y-const для механической энергии. 8 задачи 16. 1. Дело в движении Кеплера.
Найти Уравнение-Построить Годограф 3 случайная точка скорости траектории Кеплера. Определите модуль скорости в любой точке пути. Решение. Единичные векторы радиального и абсциссой оси-ex и ex. Тогда скорость движения точки в плоскости выражается компонентами полярной системы координат. Для le1ГФеа, это 1pf 21p. 1 Найти проекцию скорости на оси полюса Отрегулируйте с движением Кеплера.
При движении под действием силы центра проекция ускорения точки в поперечном направлении равна rf 2ф0, и, наконец, это 2 Интеграл площадей. Заметим, что для того, чтобы найти проективную скорость на радиальной оси, существует 2 уравнения поперечного сечения конуса, от 2 до 3, а в dtp l найти dr pesin. Если вы умножите ecosy 4 и 6, Вы будете re sin sin ce-dn y r 1 ec0sy p согласно 3 и 5. Добавляя уравнения от 1 до 2 и 7, замените v-sin pex-j-у или r 5 согласно y e sin y i 1 e cos y ea можно найти. 5 6 7 8 x начертите начало полярной системы координат на оси y.
Потом овес поляков и Декартовы координатные оси 1eiei cosysinyr-sinycosy если спроецировать скорость 8 на декартову ось, то вы найдете vx-sin sin, t j, y e cozy. Исключите углы из этих уравнений получает уравнение годографа ia уравнения 5 для y, y 0, 9. С другой стороны, рассмотрим 7, 2 и 5, чтобы преобразовать последнее уравнение из 1 в следующий вид. Определите коэффициент скорости в каждой точке траектории yepler с радиусом r. Если вы представляете значение скорости в p0 с o0, вы получаете 10 из 11 с учетом 0. Представляет Для краткости равенство 9-v, — ey. Формат r переписывается заново. 12 уравнение 12 представляет собой уравнение окружности с радиусом r.
Для полюса ходжеграфа скорости находятся на окружности. Траектория точки представляет собой параболу. В e 1 полюса ходжеграфа скорости находятся внутри круга. Траектория представляет собой эллипс. Для e 1 полюса графика скорости hod находятся вне окружности. Орбита-это гипербола. Все 3 случая показаны на рисунке. a. Соответствующее положение точки на траектории показано на рисунке. b. Из уравнения 11 определите коэффициент скорости.
Если точка находится на расстоянии r от центра тяжести, то она соответствует параболической trajectory. To сделайте это, введите e 1. Затем для 13-параболического движения найдите границу. Ввести значение от 10 до 13 r0 p 2 скорость при p 0. So, для vb 2r, v0 2r и v 2r точки представляют собой эллипсы, параболы или гиперболы соответственно. Точка ускорения Он направлен параллельно касательной hodgepodge. As в результате угол vmp равен полюсному углу, а скорость z направлена вдоль оси абсцисс. Линия вектор скорости экрана для фигуры Вектор скорости в апогее—отрезок ОД, который относится к перигею. Задача 16. 2.
Скорость планет, которые совершают движение Кеплера, разбивается на 2 составляющие. Радиаторы вектора g и-перпендикулярны главной оси эллипса. Определите модуль этих составляющих скорости и докажите, что это разложение непосредственно дает полярографы Скорость. Решение. Разложение скорости планеты на радиальную и поперечную составляющие Гfу -, 1 2 в формуле i указывается r2f g, являющийся Интегралом площади. Вывод формулы 2 дано в предыдущем задании-формула 7.
Разложим скорость планеты на составляющие, перпендикулярные радиус-вектору r и og, перпендикулярные главной оси рисунка. а. Уведомление если вы подтвердите, что угол, образованный o2, равен углу полюса, Н1пф-кцсоаф, и введете значения 1 и 2 в эти уравнения, вы получите Направление, компонент o-постоянная по модулю. Давайте отложим эту цифру. От вектора b om и его конца вектор vb перпендикулярен радиус-вектору d. Сумма этих векторов равна Угол наклона вектора к скорости планеты и продолжение om будут равны полярному углу f. Когда планета движется, то конец вектора c рисует окружность с радиусом m центра m. Это будет мешанина скорости. Задача 16. 3.
Космический аппарат массой m будет запущен ракетой на расстоянии r0, o0 от центра Земли. Момент отрыва, радиус-вектор Сформировали выбранное фиксированное направление и угол 0, скорость устройства составила 0, а угол с горизонтальной осью-60. Найти параметры орбиты космического аппарата Эксцентриситет e, параметр кривой p, угол, образованный выбранным фиксированным направлением и фокальной осью кривой pv. Solution. To создайте дифференциальное уравнение движения Для космического аппарата мы используем проекцию ускорения на полярную ось. Проекция радиального ускорения, g-gf. 1 проекция ускорения на ось абсцисс равна k Задача 16. 3. F gf 2 f.
- Ньютоновская гравитационная проекция на ту же ось равна f f−0. И дифференциальные уравнения движения в проективном. Эти оси будут gfa dg 4 rf 2lr 0. Если вы перепишете формулу b в 4 и интегральную форму, вы получите 1pf-21n r 1n s, или rfs const. 6. Таким образом, равная скорость сектора равна constant. By иду Кроме того, путем введения в уравнение 4 до 1 г, 6 д д 1 ю АКДС 1 ду ду ду ДТ ду АКДС АКДС ДТ у ДТ с дисквалификацией пр-dfdux д у длп РА Д т ДТ ДТ АКДС учитывается вводя это значение Г в уравнение ДТП 8 9 с учетом 4-6, находим дифференциальное уравнение движения космического аппарата, введенное с обозначением Р С4 х.
Уравнение 10 Коэффициент представляет собой постоянное, неоднородное линейное дифференциальное уравнение 2-го порядка. Решение состоит из общего решения однородного уравнения и частного решения Полное уравнение. Заметим, что корень характеристического уравнения является чисто мнимым z1, чтобы найти общее решение однородного уравнения. Конкретное решение полного уравнения u поэтому решением дифференциального уравнения 10 является y-cm cos p-ct sin p, или i 1 1-ecoa f-ph1-llp. Где cj и cg или в и pi-константы, соответственно. Интеграция. Возвращаясь к исходной переменной r, находим орбитальное уравнение конечного вида r 1-cos — 12 12.
Как и в двух предыдущих задачах, начало отсчета расположим в положении статического равновесия и ось х направим по вертикали вниз. Людмила Фирмаль
Первая форма записи локуса и константы e, p2 — это 2-я форма записи. Если переписать формулу 12 в формат 1 2-c03 f-f1 и сравнить ее с 11, то получится cl cos f ct sin f c08 f-fg. Отсюда 14 15 здесь мы переходим к прямому определению зависимости параметров траектории от начальных условий движения. 7, согласно 16gm, с одной стороны, проекция скорости Поскольку горизонтальная ось равна t-d0cose0sr0 p0, 17, введем безразмерную величину, равную отношению кинетической энергии точки, движущейся вдоль p-18 Кеплера Траектория Ньютона к потенциалу. Rm 2 v r 1-r 2 q с последующим 18 записывается в виде 19. 20 это 2-е выражение параметра кривой для начального условия движения.
Для Вводя это значение производной в выражение cj cos f cg 1p f-11 из остальных 2 параметров, получаем Сsinф -oscosф—. Это равенство в отношении Переменные, ci sinф-С1 drtrdf 22 0c0s8 dtГ23Гtgе. Решите 24 21 и 26 вместе, и c-с — — ycos q-sinф, —ij sinф4 —y cos f. Двадцать шесть 27 Итак, согласно 14, 1-это Иисус. 28 используйте 20, чтобы передать его в параметр ab. Затем es-1-2 cos1b 2lx cos 6 sin fl 2 8 или, наконец, e 1-4 1-aj cos 0. 29 наконец, согласно 16 и 26, 27, tern-c-sinph 8cosph wu1 ci g-p c0s p-pig6 sin p 30 выражения 20, 29 и 30 представляют искомые зависимости параметров p, e, q 1. От начального состояния движения.
Используя эти уравнения, можно установить зависимость характера траектории от начальных условий движения. Motion. In факт, пожалуйста, рассмотрите возможность использования Это 3 уравнения, условия, при которых космический аппарат будет двигаться по 5 траекториям Кеплера 1. Линейный путь возможен согласно уравнению 1 17 Если во все моменты движения, а следовательно, и в первый момент 31 2, время первого момента 6 0, Время всего движения, включая 32 Т, циркуляционный путь возможен. Скорость-это касательное направление окружности. Однако это условие, которое выполняется в первый момент, необходимо, но недостаточно.
Из уравнения 12 модуль равен если эксцентриситет e равен нулю, то радиус-вектор точки не изменяется, принимая во внимание 29-32, e1 sin 6 1-2 cos 0 1-0 в соответствии с уравнением 19, это условие Вы можете написать, где появилась первая космическая скорость from. In факт, что r жив. R-радиус Земли, а p r-километровая секунда. 35 Итак, космический Спутник должен превратиться в искусственный спутник Земли, двигаясь по круговой траектории вблизи поверхности Земли, удовлетворяя 2 отдельным условиям 35 и 32. Космос Поскольку устройство описывает круговую орбиту на расстоянии th от поверхности Земли, его скорость равна sze в соответствии с 34.
Эта скорость является Она получается путем проецирования уравнения движения по круговой орбите непосредственно на нормали w n fn. Или, предполагая r0 r b, это будет снова 36. 3 параболическая траектория 29 по космическому аппарату, который в данном случае является Е-1, так что это будет 1. С 19 будет ВС -. Скорость v2 называется параболической скоростью. Космос Устройство, уведомленное в первый момент об этой скорости, не возвращается на Землю. Когда r равно 0, мы получаем 2-ю космическую скорость t 2 v 2gr i 11, 2 км сек. 4 овала Согласно 29, орбита равна 0 lx 1 и e 1, поэтому единственными исключениями в этом случае являются 1 2 и 0 0.
Показано, что устройство движется по круговой траектории. Скорость Космический корабль в этом случае должен находиться в пределах 5. Согласно 29, гиперболическая траектория космического аппарата будет kl i, поскольку в этом случае 1. Космический аппарат в этом случае должен находиться таким образом, а параметры, равные соотношению кинетической энергии и потенциала, определяют характер траектории движения космического аппарата. Отзыв Ньютоновский потенциал определяется уравнением 3 u y. So, если кинетическая энергия точки единичной массы меньше потенциала Ньютона, то точка равна Она бесконечна и представляет собой замкнутый путь, эллипс вокруг центра притяжения.
Если кинетическая энергия больше или равна ньютоновскому потенциалу, то точка удаляется при Бесконечность вдоль параболы или гиперболической траектории. Задача 16. 4. Ракета-носитель доставила космический аппарат с поверхности земли на высоту h Далее движение Кеплера, начальная скорость которого направлена под углом 8 градусов относительно местного горизонта, см. Иллюстрацию. Определить модуль начальной скорости М орбиты Скорость М проходит вне Земли — 2-я космическая скорость 1. Решение.
Найти и задать минимальное значение радиус-вектора из уравнения траектории движения Кеплера — p1 1, откуда r-r g. — Гт-rmln-траектория рассматриваемого устройства, в зависимости от величины и 80, может не проходить или проходить через поверхность Земли. Очевидно. Hpnp или tt7-Н. В. Бутенин, А. Г. Безонов, Е. М. Морозов, введение в деление твердых тел, движущихся в поле Серьезность. Основы астрономии. Ленинградский авиационный приборостроительный институт, 1965.
Предполагая, что в условии указано 80, он находит минимальное значение color1. Орбита аппарата будет представлять собой орбиту искусственного спутника Земли. В соответствии с 20 и 29, p r l или p-r e2r2, выражают p и e через начальные условия движения. Бывший Вача. Затем найдите 2-й g0 cos 80-r 2 sin fl0 1-2ax 2 cos 80 r. 4ajcos чтобы открыть кронштейн и сократить 90 не ноль, вы получите 1 rjcos eo-r2 В параметре kx со значением предыдущей задачи 19 учитывается r0 r b, Г2м01МЛГr a c0s 0o-r2. Для начальной скорости vo vol и coseo j траектории не пересекаются. Поверхность Земли.
Если начальная скорость равна t 0 или cos0o, то траектория будет пересекать поверхность Земли, и устройство будет баллистической ракетой, а не искусственным спутником Земли. Обратите внимание, что в Л0 скорость ti0i может существовать только в 80 0. Если мы выявим неопределенность под 2-м радикалом, то увидим, что она равна 1. — Первая космическая скорость. Задача 16. 5. Космический аппарат, движущийся под действием силы тяжести вблизи Земли, в первый момент времени имеет радиус-вектор r0 и скорость t. 0. Определите модуль скорости блока на любом time. Solution. To найти коэффициент скорости в любое время, применить теорему изменения кинетической энергии.
Увеличение кинетической энергии при смещении основания равно элементарной работе силы тяжести m. Уменьшение массы m, интегральной от начальной скорости к скорости Таким образом, коэффициент скорости в любой точке траектории определяется уравнением 1, в любом положении траектории, слева и справа от r0Дг. Это выражение является Движение прибора по траектории Кеплера является прямым, круговым, эллиптическим, параболическим и гиперболическим, так как при выводе на него не накладывается никаких ограничений. Если Траектория движения аппарата заканчивается у поверхности Земли, а коэффициент скорости в момент падения определяется по формуле, где r-радиус Земли.
При движении по Кольцевой дороге Согласно 1, коэффициент скорости не изменяется. Задача 16. 6. 5 орбит Кеплера определяют наибольшую высоту полета космического аппарата, движущегося вдоль ивы. Решение. Рассмотрим отдельно движения Кеплера по каждой траектории. Радиальная орбита. Когда космический аппарат движется по прямой радиальной орбите, устройство находится Достигните максимального расстояния от Земли в тот момент, когда ее скорость исчезнет. Если вы воспользуетесь Формулой 1 предыдущей задачи, то скорость v будет равна нулю, и вы увидите максимальное расстояние.
Здесь, как и прежде, отношение кинетической энергии начального момента к работе, которую необходимо затратить, чтобы переместить устройство из начального состояния в бесконечное. Максимальная высота полета на поверхности Земли lo 1 будет тогда, когда аппарат не вернется на Землю. Круговой orbit. In в этом случае высота полета не изменится. Эллиптическая орбита. При движении по эллиптической орбите минимальная высота называется перигеем, а если вся орбита находится вне Земли, то наибольшая высота называется апогеем. От Орбитальное уравнение П. .1-экстремальное значение радиус-вектора Равно08-ф1 .Поэтому максимальная и минимальная высота Над поверхностью Земли будет находиться-fJ.
Смотрите также:
Предмет теоретическая механика

