Оглавление:






Влияние гироскопических сил и сил вязкого сопротивления на свободные и вынужденные колебания твердого тела с двумя степенями свободы
- Влияние силы гироскопа на свободную вибрацию системы 2 степеней свободы. При создании дифференциального уравнения для малой вибрации учитывается сила гироскопа. Применим теорему к изменению главного момента импульса для фиксированных координатных осей. Где l ly, l-основные моменты импульса относительно неподвижных осей координат x, y, z. V i ff — основной момент внешней силы относительно той же оси.
Если осесимметричное твердое тело с неподвижной точкой вращается вокруг оси симметрии с большой угловой скоростью w, то это совпадает с неподвижной осью x, когда тело находится в равновесии. Тогда основной момент импульса для фиксированных осей координат будет равен dx ao, ly ai c, r ashu b1z 2 Где А-момент инерции твердого тела относительно оси symmetry. It является также моментом инерции для любой оси, проходящей через неподвижную точку Р, перпендикулярную оси симметрии.
Существует проект запуска трех искусственных спутников па эту высоту так, чтобы они образовали равносторонний треугольник, в вершинах которого находились бы спутники. Людмила Фирмаль
Маленький угол поворота оси симметрии, измеренный от неподвижной оси x плоскости xy, m-малый угол поворота оси симметрии, измеренный от неподвижной оси x плоскости x x плоскости xz. Нейпьидо Система координат-стационарная и мобильная Родственник Движение Фиксированные оси, связанные с ними 3 найти дифференциальное уравнение малых колебаний системы, используя теорему об изменении главных моментов импульса относительно осей x, y и z. 4 найти конкретное решение системы и отнести его к дифференциальным уравнениям движения.
Найти частотное уравнение, определяющее собственные частоты системы. 5 кроме того, найти отношение амплитуды колебаний, соответствующих каждой частоте. 6 Создайте 1-е и 2-е уравнения колебания СФ Ось с использованием углов и y. Составляющая угловой скорости Ротора выглядит так, она направлена к оси оси oc, она направлена вдоль оси 0, z, а y направлена к отрицательной стороне Оси o. Найти угловую проекцию Скорость вращения ротора на инерционном шпинделе a, b, c — Т. — Предполагая углы p и y и их производные в малом количестве 1-го порядка, находим значение проекции главной угловой скорости. Точность оси инерции является всеобъемлющей.
В первом небольшом количестве Порядка 2 Основными моментами количественного движения относительно инерциальной главной оси abc являются И. -ЛБ-Б ЛНР а я. 3 Далее находим проекцию основного момента импульса па. , x lc cos 1 cos 3-l. A sinf cos — Я грешу Р Де — ly l. t cos 7 sin — Л Сих 7 Грехов Потому что ЛГ 3. 4юз-Р 7 — Более i. C sin 7 4 —. Cos 7 ИД017 — — 33. 4 Биологически отбросьте термин, приводящий к небольшому порядку. L, au, i. R ash3-b -, 1. R au и t 5 5 часов вечера. Проблема 454. Шпиндель шпинделя зафиксирован в точке О так, что он не двинет, и он вращает с упруго прикрепленным подшипником А. Центр gravity. .. It находится на расстоянии 1 от точки с Рис.
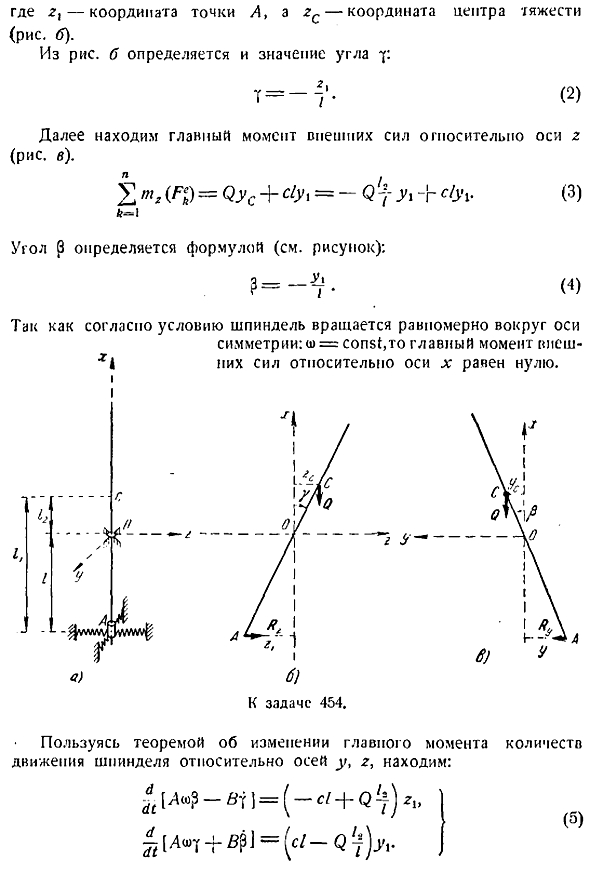
- Точки между спорами. Коэффициент жесткости от упругого поля, нижняя опора Т смешивается. Момент инерции к главной оси инерции через точки o, a, b находит малое колебание шпинделя вблизи положения равновесия. Угловая скорость o окрашивание Размер шпинделя вокруг оси симметрии постоянна. Решение. Выберите неподвижную координатную ось xyz рисунок a, центрированную в неподвижной точке О, и направьте вертикальную ось x вдоль шпинделя и ось симметрии в симметричное положение. Внешняя сила воздействует на шпиндель реактивная сила r опоры a, реактивная сила опоры o и сила q.
Настраивает основные моменты всех внешних сил относительно осей t x, y, z для уменьшения шпинделя отклонение угла па вокруг оси z 3 и угла па вокруг каждого 7 главные моменты внешних сил на оси y Где z-координаты точки рисунок b. Определяется из рис. А 2-это координата центроида и значение угла у. 2 Далее находим основные моменты внешней силы на оси рисунок с. Преобразуйте эти уравнения, заменив их на y и 2t вместо p и y. Тогда вы получите Р5, — Д — — -qlt з 0 АР dshg, — — Ци, г, о. 6 Это дифференциальные уравнения малых колебаний шпинделя.
Подставив это значение цл1 в формулу (4) предыдущей задачи, находим: откуда искомая высота Подставив численные значения, найдем, что искомая высота равна 36 800 км. Людмила Фирмаль
Решение этой системы однородных линейных дифференциальных уравнений с постоянными коэффициентами может быть найдено в следующем виде У1 Асин п с — j-А, З Б сов пт —. 7 Присвоим значение переменной уравнению 6, где sin p -y-a и cos pi- если свести их с-а, то получится система алгебраических уравнений для определения констант. — Отверстие s 5-q j-brg b 0 cp-qlt-bp a-dpbb-0. Колебания Легче, чем кто-либо другой. Склав Небольшая замена формулы 8 на определение собственной частоты этих корней, амплитуды колебаний Часть частотного уравнения 8 уравнения 9 имеет следующий вид cp-qlt-yar1-hole a b 0, 1 cp-qlt-bp1 отверстие a-i 0. У Есть 2 вида основной вибрации или нормальной вибрации на шпинделе.
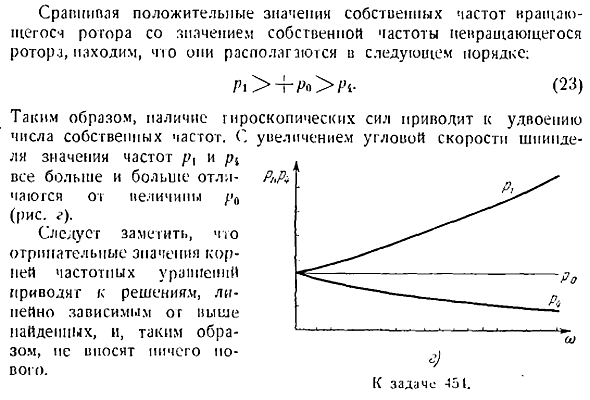
Частота первого основного колебания определяется по формуле ВР — АТОР— СР-qlt 0. 11 Если мы решим это квадратное уравнение, то сможем увидеть частоту 4 4fi все КЗ — г с ——— 12 Значение частоты 12, поэтому коэффициент первого уравнения Если отключить первые со, то они соответствуют равенству Найти частоту 2-ой основной вибрации Грушевый сидр. 18 Секунда и Шаг Ротора, вибрация характеризуется формулой Частота 15 1 Без сомнения, вы заплатите пулю первым Прерывание определяется по формуле Ом-м. Р — со П, Т 4-а. 19 При первом типе колебаний точка А представляет собой окружность вокруг центра по оси x. Вращение точки А совпадает с правильным вращением и направлением вращения ротора.
Это движение эго называется прямой прецессией. Во 2-м типе вибрации точка a представляет собой окружность вокруг центра, которая пахнет в противоположном направлении от оси x Уникальное вращение ротора. Это движение называется обратной прецессией. Общим решением дифференциального уравнения для определения свободных колебаний Ротора является 2 основных колебания i sin p al — i-o1sin p, ti-a1, 1 g, cos p4 4-a, — a, cos Ом 4 — q.
Смотрите также:
Предмет теоретическая механика

