Оглавление:
Термодинамика
Термодинамика — это раздел физики, изучающий связи и преобразования тепла и других форм энергии. Термодинамика — это феноменологическая наука, основанная на обобщении экспериментальных фактов. Она изучает макроскопические системы, состоящие из огромного количества частиц — термодинамические системы. Процессы, происходящие в таких системах, описываются макроскопическими значениями, такими как давление или температура, которые не применимы к отдельным молекулам и атомам.
Первое начало термодинамики
Введение
Первое начало термодинамики выражает принцип сохранения энергии для тех макроскопических явлений, в которых одним из существенных параметров, определяющих состояние тел, является температура. Его открытие относится к 40-м годам XIX века, когда было установлено, что теплота — не вещество, а какое-то внутреннее движение тела.
Возможно эта страница вам будет полезна:
| Предмет термодинамика |
В механике энергия складывается из кинетической энергии макроскопического движения и потенциальной энергии макроскопических тел во внешних силовых полях. В механике доказывается, что для изолированной системы полная механическая энергия сохраняется, т. е. ее количество остается неизменным. Но это справедливо не всегда. а только в тех случаях, когда все действующие в системе силы консервативны.
При наличии диссипативных сил — сил трения — механическая энергия замкнутой системы уменьшается. Однако опыты показали, что работа диссипативных сил всегда сопровождается выделением теплоты.
Оказалось, что принцип сохранения энергии остается справедливым и при наличии диссипативных сил, если только расширить понятие энергии введением новой формы ее, а именно внутренней энергии, называемой также (не совсем удачно) тепловой энергией. Это было сделано Майером (1814-1878), Джоулем (1818-1889), Гельмгольцем (1821—1894) и другими учеными, с именами которых связывают открытие принципа сохранения энергии в его общефизическом смысле.
С атомистической точки зрения нарушения механического закона сохранения энергии объясняются тем, что макроскопическая механика учитывает не все движения и силовые взаимодействия. Из ее поля зрения ускользают внутренние невидимые движения отдельных атомов и молекул, а также силы взаимодействия между ними. Диссипативные силы годятся только для описания макроскопических движений.
В мире атомов и молекул никаких диссипативных сил не существует, все силы консервативные и гироскопические.
Всякое тело с атомистической точки зрения является консервативной системой колоссального числа частиц — атомов и молекул. Для такой системы механический закон сохранения энергии справедлив, но только при непременном условии, что к энергии макроскопического движения добавляется энергия беспорядочного атомно-молекулярного движения. Это последнее движение и есть теплота.
Однако последовательная феноменологическая термодинамика должна вводить расширенное понятие механической энергии, не обращаясь к атомистическим представлениям, руководствуясь одними только общими принципами, являющимися обобщениями опытных фактов. Ближайшей нашей целью и является введение этого понятия.
Возможно эта страница вам будет полезна:
| Задачи по термодинамике |
Квазистатические процессы
В теоретических методах термодинамики широко используются так называемые квазистатические, или квазиравновесные, процессы, т. е. идеализированные процессы, состоящие из непрерывно следующих друг за другом состояний равновесия.
В качестве примера возьмем цилиндр с поршнем, который может свободно перемещаться в нем без трения. Пусть в цилиндре находится газ и поршень удерживается в положении равновесия лежащим на нем грузом 
(рис. 6). Если снять часть груза или добавить новый, то равновесие нарушится.
Возникнет довольно сложное движение газа и колебания поршня с грузом. Но в конце концов все эти движения затухнут, и рассматриваемая система вновь придет в состояние равновесия.
Подобные неравновесные процессы очень сложны. Квазистатические процессы несравненно более просты. Чтобы заставить газ в цилиндре расширяться или сжиматься квазистатически, допустим, что разгрузка или нагрузка поршня идет бесконечно малыми порциями.
наглядности можно вообразить, что поршень нагружен мелким песком. Снимем или добавим одну песчинку. От этого равновесие нарушится бесконечно мало. Когда оно восстановится, снимем или добавим вторую песчинку. Повторив эту операцию много раз, можно в конце концов снять весь груз или изменить его на любую конечную величину.
Вместе с грузом изменится на конечную величину и объем газа. Этот процесс состоит из последовательности бесконечно малых процессов, каждый из которых лишь ничтожно мало нарушает состояние равновесия.
В пределе, когда масса каждой песчинки стремится к нулю, а полное число песчинок — к бесконечности, получится бесконечно медленный процесс, состоящий из последовательности равновесных состояний. Такой предельный процесс называется равновесным.. Логически равновесный процесс надо отличать от квазиравновесного, или квазистатического, процесса.
надо иметь в виду, что строго равновесный процесс никогда не реализуется в природе. Поэтому в большинстве рассуждений квазиравновесный процесс называют просто равновесным, опуская приставку «квази». Это будем делать и мы, когда такое сокращение не вызывает недоразумений.
Значение квазистатических процессов состоит в том, что они сильно упрощают термодинамические исследования. Это объясняется тем, что для мгновенного описания состояния системы, совершающей квазистатический процесс, требуется столько же параметров, сколько и для макроскопического описания равновесного состояния.
В случае газа таких параметров два, например объем и температура. Для более сложных систем число параметров может быть другим, но, если процесс квазистатический, оно, как правило, невелико.
Напротив, для описания состояния системы, совершающей какой-либо сложный неквазистатический процесс, например турбулентное движение жидкости или газа, требуется, вообще говоря, бесконечное множество даже макроскопических параметров.
Квазистатические процессы в строгом смысле этого слова никогда не реализуются в природе. Они являются абстракциями. Но к ним можно подойти сколь угодно близко. Очень многие реальные процессы, идущие с конечными скоростями, часто могут считаться приблизительно квазистатическими.
‘Гаковы, например, процессы расширения газов в цилиндрах тепловых двигателей или компрессоров. Образование сгущений или разрежений воздуха в звуковой волне также может рассматриваться как приблизительно квазистатический процесс. Конечно, не всякий медленный процесс является равновесным. Примером может служить процесс теплопроводности.
В термодинамике часто встречаются следующие квазистатические процессы:
- 1) изохорный процесс — процесс, происходящий при постоянном объеме (
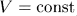); - 2) изобарный процесс — процесс, в котором давление остается постоянным (
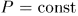); - 3) изотермический процесс — процесс, происходящий при постоянной температуре (
).
Как и все квазистатические процессы, указанные процессы можно графически изобразить непрерывными линиями (см. следующий параграф). Соответствующие кривые называются изохорой (), изобарой () и изотермой ().
Макроскопическая работа
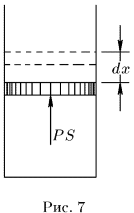
1. Рассмотрим снова газ в цилиндре с поршнем (рис. 7). Вычислим бесконечно малую или элементарную работу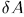 
, совершаемую газом при бесконечно малом квазистатическом расширении, в котором его объем увеличивается на 
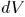. Сила давления газа на поршень равна 
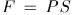, где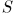 
— площадь поршня. Если поршень переместится на расстояние 
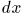, то газ совершит работу 
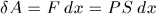или
так как приращение объема равно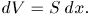 
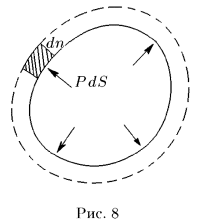
Выражение (12.1) справедливо и в общем случае квазистатического изменения объема любого тела, находящегося под постоянным внешним давлением. Допустим, например, что газ заключен в мягкую эластичную оболочку и эта оболочка квазистатически расширяется (рис. 8). Работа, совершаемая газом при перемещении элемента площади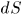 
оболочки на расстояние 
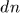вдоль нормали, равна 
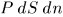, или 
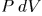, где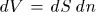 
— элементарный объем, заштрихованный на рис. 8. Чтобы найти элементарную работу при перемещении всех элементов оболочки, надо выражение 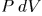проинтегрировать по объему слоя между двумя последовательными бесконечно близкими положениями оболочки. Так как давление 
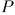одно и то же по всей оболочке, то его можно вынести из-под знака интеграла.
Таким путем получится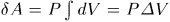 
, где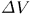 
— объем вышеуказанного слоя, равный приращению объема газа в рассматриваемом процессе. Введя для него прежнее обозначение 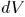, мы снова придем к формуле (12.1). Для применимости вывода несущественно, что в оболочке помещен газ. Вывод справедлив для любого вещества, находящегося под постоянным давлением. Несущественно также наличие оболочки. Ее роль может играть поверхность тела.
В случае квазистатических процессов внутреннее давление 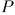газа в пределе всегда равно внешнему давлению на поршень 
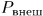. Только тогда внутреннее состояние газа может быть охарактеризовано двумя параметрами и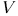 
, и только тогда процесс может быть равновесным и идти бесконечно медленно.
В противном случае возникает ускоренное макроскопическое движение поршня и частей газа с конечными скоростями и для описания внутреннего состояния газа потребуется бесконечное множество параметров. Если процесс неквазистатический, но внешнее давление по всей поверхности системы одно и то же, то работа внешних сил представится выражением
Для квазистатических процессов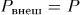 
, а потому 
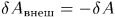. (В общем случае работа тела 
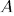над телом 
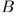не равна работе тела 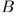над телом 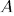.) В случае неравновесных процессов, происходящих с ускорением, это, вообще говоря, несправедливо и для работы системы нельзя написать никакого простого выражения.
Таким образом, формула (12.1) относится только к случаю квазистатических процессов. В этом параграфе предполагается, что все процессы — квазистатические.
Чтобы от элементарной работы 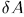перейти к работе для конечного процесса, надо вычислить интеграл
Однако такое вычисление возможно только тогда, когда давление является определенной функцией объема 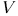. Между тем, согласно
уравнению состояния, 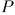зависит не только от 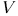, но и от 
.
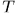Меняя в ходе процесса различным образом температуру системы, можно квазистатически перевести систему из начального состояния в конечное бесчисленным множеством способов. Каждому из этих способов соответствует своя функция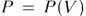 
и свое значение интеграла в формуле (12.3).
Таким образом, работа 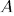не определяется заданием начального и конечного состояний системы. Ее величина зависит также от способа или пути перехода системы из начального состояния в конечное. Про величины такого рода говорят, что они не являются функциями состояния. Напротив, величины, имеющие вполне определенные значения в каждом состоянии системы, называются функциями состояния. Такова, например, температура системы в состоянии термодинамического равновесия.
Разобраться в существе дела проще всего с помощью графического метода. Он использует то обстоятельство, что равновесное состояние физически однородного и изотропного тела полностью определяется заданием двух параметров, например 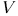и .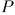
Температура 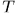может быть найдена по ним из уравнения состояния 
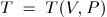. Состояние тела задается точкой на координатной плоскости, причем по горизонтальной оси откладывается объем 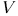, а по вертикальной — давление 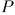. Такая плоскость для краткости называется плоскостью .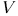
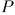Когда система совершает квазистатический процесс, точка, изображающая ее состояние, описывает на плоскости 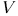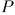непрерывную линию. Таким образом, квазистатические процессы изображаются непрерывными кривыми.
Вместо переменных 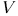, 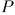можно пользоваться переменным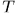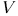и , или 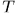, 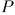. Однако для графического представления работы наиболее удобны переменные 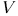, 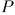. Неравновесные состояния и неравновесные процессы нельзя изображать точками и кривыми на плоскости, так как для задания неравновесного состояния двух параметров недостаточно. Неравновесные состояния характеризуются, вообще говоря, бесконечным множеством параметров.
Пусть система квазистатически переходит из состояния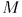 
в состояние 
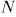вдоль кривой 
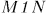(рис. 9). Эта кривая определяет давление 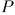как вполне определенную функцию объема 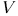. После этого работа системы 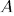определится однозначно.
Она численно равна площади «криволинейной трапеции»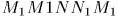 
. Если систему заставить переходить из того же начального в то же конечное состояние вдоль другой кривой 
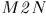, то соответствующая работа 
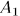изобразится другой площадью 
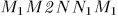. Вообще говоря, 
.
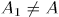Вычислим, например, работу, совершаемую одним молем идеального газа при изотермическом расширении (т. е. при таком расширении, когда температура газа поддерживается постоянной). Для наглядности представим себе газ, заключенный в цилиндр с поршнем, на котором находится груз.
Будем бесконечно медленно и непрерывно уменьшать нагрузку на поршень и в то же время подогревать газ, чтобы обеспечить постоянство его температуры во время расширения. Графически процесс расширения газа изобразится на плоскости 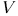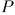гиперболой 
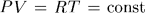, (рис. 10). Работа, совершаемая газом,
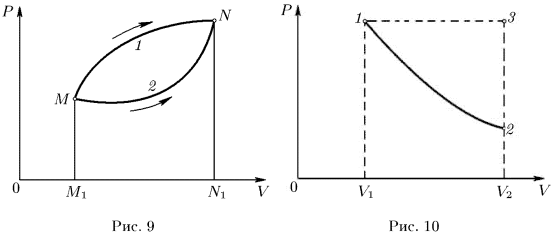
Можно перевести газ из начального состояния 1 в конечное состояние 2 бесчисленным множеством других способов. Например, можно, сохраняя давление газа постоянным (т. е. не изменяя нагрузку на поршень), нагреть газ, доведя его объем до значения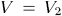 
. Этот процесс на рис. 10 изображен горизонтальной прямой 1-3; при этом газ совершит работу 
.
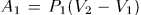Затем, закрепив неподвижно поршень и охлаждая газ, можно довести его давление до значения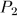 
. Этот процесс происходит без совершения работы: на рис. 10 он изображен вертикальной прямой 3-В результате система перейдет в то же конечное состояние 2, совершив работу 
.
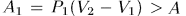Приведенный пример наглядно показывает, что работа зависит не только от начального и конечного состояний, но и от способа (или пути) переходя системы из одного состояния в другое. Значит, работа не есть функция состояния.
Если в результате изменений система вернулась в исходное состояние, то говорят, что она совершила круговой процесс, или цикл. Такой процесс, если он квазистатический, на диаграмме 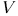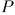изображается замкнутой кривой (рис. 11).
Работа, совершенная системой в круговом процессе, численно равна площади цикла, заштрихованной на рис. 11. При этом если точка, изображающая состояние системы, описывает цикл по часовой стрелке, то работа системы положительна. Если же цикл проходится в направлении против часовой стрелки, то она отрицательна.
5. Мы нашли выражение для элементарной работы и выяснили свойства этой величины на примере газа или изотропного однородного тела, находящегося под постоянным внешним давлением. Внутреннее состояние таких систем определяется двумя параметрами, например 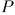и .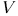
Поэтому их можно называть простыми системами или системами с двумя степенями свободы. Могут быть системы со многими степенями свободы, внутреннее состояние их определяется температурой 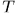и какими-то внешними макроскопическими параметрами 
.
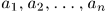В этом случае работа по-прежнему зависит от пути перехода, однако вместо формулы (12.1) следует писать
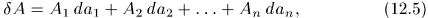
где для квазистатического процесса используются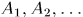 
— функции параметров 
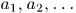и температуры 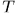, называемые обобщенными силами. Рассмотрим, например, прямоугольный параллелепипед из однородного изотропного вещества (рис. 12). Если на его грани действуют нормальные давления 
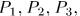то элементарная работа, совершаемая системой, представится выражением
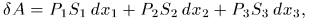
где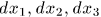 
— удлинения ребер параллелепипеда, a 
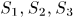— площади соответствующих граней. Обобщенные силы определяются выражениями
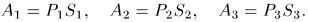
Первое начало термодинамики для системы в адиабатической оболочке
Пусть термодинамическая система заключена в какую-то оболочку, отделяющую ее от других тел. Различные части оболочки могут перемещаться. Примером может служить цилиндр с поршнем, в котором находится газ. Изменять состояние системы внутри оболочки можно различными способами.
Один из них состоит в механическом перемещении частей оболочки или, вообще, в изменении внешних параметров, определяющих наряду с температурой внутреннее макроскопическое состояние системы. Этот способ, как правило, сопровождается производством механической работы.
Работа внешних сил, связанная с перемещением оболочки или с изменением внешних параметров, называется макроскопической работой, производимой над системой. Эту величину мы обозначаем буквой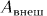 
в отличие от работы, производимой самой системой, которая обозначается через 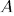. В предыдущем параграфе приводились формулы для вычисления работы 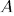или 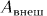при квазистатических процессах. В этом случае всегда 
. Теперь рассматривается более общий случай, когда процесс не обязательно квазистатический. Для такого процесса, вообще говоря,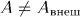 
.
Не надо думать, что производство работы обязательно связано с изменением объема системы. Так, в общеизвестных опытах Джоуля по определению механического эквивалента теплоты лопасти мешалки являются составными частями оболочки, в которую заключена система, например вода. При вращении мешалки над системой совершается механическая работа. Она проявляется в нагревании воды в калориметре.
Внутренняя энергия
Внутренняя энергия является одной из важнейших величин, характеризующих систему в состоянии термодинамического равновесия. Поэтому мы будем здесь предполагать, что начальное и конечное состояния системы равновесны. Однако процессы, переводящие систему из одного состояния в другое, а следовательно, и промежуточные состояния, вообще говоря, могут быть и неравновесными.
Внутренней энергией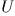 
системы, называется, функция состояния, приращение которой во всяком процессе, совершаемом системой в адиабатической оболочке, равно работе внешних сил над системой при переходе ее из начального равновесного состояния в конечное, также равновесное состояние.
Возможность введения такой функции состояния основана на том, что работа над системой в адиабатической оболочке зависит только от начального и конечного состояний системы, но не зависит от способа перехода. Начальное состояние мы будем обозначать индексом 1, конечное — индексом 2. Таким образом, если система помещена в адиабатическую оболочку, то
где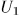 
и 
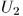— внутренние энергии системы в состояниях 1 и 2, а 
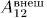— работа, производимая над системой внешними силами при переходе ее из состояния 1 в состояние 2 по любому пути.
Разумеется, слово «приращение» надо понимать не в арифметическом, а в алгебраическом смысле. Внутренняя энергия системы может как возрастать, так и убывать, а работа 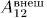может быть и положительной, и отрицательной.
Может случиться, что адиабатический переход из состояния 1 в состояние 2 невозможен. Тогда определение (14.1) теряет смысл. Но в таких случаях, как подчеркивалось в предыдущем параграфе, возможен обратный адиабатический переход из состояния 2 в состояние 1. Им и надо воспользоваться для определения изменения внутренней энергии, т. е. вместо формулы (14.1) следует писать
Таким образом, используя либо адиабатический переход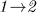 
, либо обратный адиабатический переход 
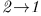, всегда можно определить разность внутренних энергий в любых равновесных состояниях 1 и 2.
Количество теплоты. Математическая формулировка первого начала термодинамики
Если система помещена в адиабатическую оболочку, то единственным способом изменить ее внутреннюю энергию является производство над ней макроскопической работы, что достигается путем изменения внешних параметров. (К числу внешних параметров относятся и силовые поля, в которые помещена система.)
Однако если адиабатической изоляции нет, то изменение внутренней энергии возможно и без производства макроскопической работы. Так, при соприкосновении горячего и холодного тел внутренняя энергия переходит от горячего тела к холодному, хотя при этом макроскопическая работа и не совершается.
Процесс обмена внутренними энергиями соприкасающихся тел, не сопровождающийся производством макроскопической работы, называется теплообменом. Энергия, переданная телу окружающей средой в результате теплообмена, называется количеством теплоты, или просто теплотой, полученной телом в таком процессе.
Изменение внутренней энергии тела во время теплообмена, в сущности, обусловлено также работой каких-то внешних сил. Но это не есть макроскопическая работа, связанная с изменением внешних макроскопических параметров.
Она является микроскопической работой, т. е. складывается из работ, производимых молекулярными силами, с которыми на молекулы и атомы тела действуют молекулы и атомы окружающей среды. Так, при приведении тела в контакт с горячим газом передача энергии от газа к телу осуществляется посредством столкновений молекул газа с молекулами тела.
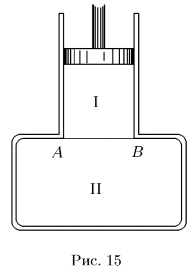
Сформулируем математически начало термодинамики с учетом теплообмена. Пусть интересующая нас термодинамическая система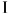 
(рис. 15) находится в тепловом контакте с какой-то системой 
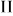. Вся система 
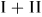заключена в адиабатическую оболочку, однако граница 
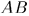между системами является теплопроводящей. При этих условиях система 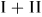не может обмениваться теплотой с окружающей средой, однако теплообмен между системам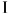и и 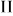может происходить. Допустим далее, что оболочка, в которую заключена система 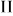, жесткая, так что никакой работы система 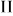производить не может. Система 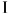, напротив, может совершать работу над окружающей средой. На схематическом рис. 15 система 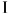изображена в виде цилиндра с подвижным теплонепроводящим поршнем. Стенки цилиндра — адиабатические, а дно 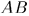может проводить тепло. Адиабатические стенки на рисунке изображены двойными линиями, проводящая перегородка 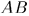— сплошной тонкой линией.
Пусть система 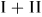перешла из произвольного состояния 1 в другое состояние 2, в результате чего системой совершена работа 
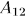над внешними телами. Эту работу совершила только система 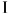. Так как составная система 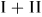адиабатически изолирована, то
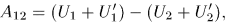
где 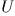— внутренняя энергия системы 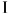, a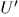 
— системы 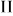. Поскольку нас интересует поведение только системы 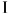, перепишем это соотношение так:
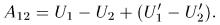
Убыль внутренней энергии системы 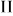есть, по определению, количество теплоты, полученное системой 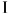в рассматриваемом процессе. Обозначим эту величину через 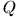. Тогда по определению
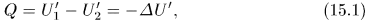
и предыдущее соотношение примет вид
Это уравнение и дает математическую формулировку первого начала термодинамики. Оно утверждает, что теплота 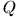, полученная системой, идет на приращение ее внутренней энергии 
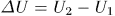и на производство внешней работы.
Методические указания по решению задач ( 1 курс)
Задача:
Идеальный газ находится в эластичной адиабатической оболочке под давлением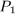 
, имея температуру 
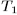. Определить температуру газа 
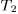, которая установится после того, как внешнее давление на газ скачкообразно изменится до 
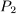. Сравнить изменение температуры в этом процессе с изменением, которое получилось бы, если бы адиабатический процесс проходил квазистатически.
Решение:
При переходе из начального состояния (объем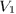 
, температура 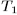) в конечное (объем 
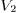, температура 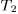) внешнее давление совершает над газом работу 
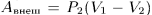, которая идет на приращение внутренней энергии 
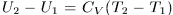. Применяя уравнение Клапейрона-Менделеева 
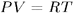, а также соотношение 
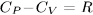, после несложных преобразований получим
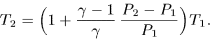
При квазистатическом адиабатическом процессе, как следует из (21.5),
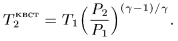
В первом случае 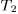меняется линейно, а во втором по степенному закону с изменением 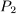, причем в бесконечно малой окрестности точки 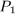оба изменения идут одинаково быстро. А так как 
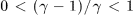, то всегда 
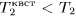. Значит, повышение температуры при внезапном адиабатическом расширении меньше, чем при квазистатическом адиабатическом процессе.
Второе начало термодинамики
Общие замечания о первом и втором началах термодинамики
Первое начало термодинамики не дает никаких указаний относительно направления, в котором могут происходить процессы в природе.
Для изолированной системы, например, первое начало требует только, чтобы при всех процессах энергия системы оставалась постоянной. Если 1 и 2 — два состояния такой системы, то первое начало ничего не может сказать, будет ли система переходить из состояния 1 в состояние 2, или из состояния 2 в состояние 1. Вообще, на основании первого начала нельзя выяснить, будут ли в изолированной системе происходить какие-либо процессы.
Пусть адиабатически изолированная система состоит из двух тел, взаимодействующих между собой, но не взаимодействующих с другими телами. ‘Тогда, как было показано в § 16, теплообмен между ними подчиняется условию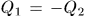 
. Теплота 
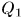, полученная одним телом, равна теплоте — 
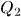, отданной другим телом.
В каком направлении будет переходить теплота — на этот вопрос первое начало термодинамики ответить не может. Первому началу не противоречил бы, например, процесс, в котором теплота самопроизвольно переходит от тела менее нагретого к телу более нагретому.
Вопрос о количественной мере температуры чужд первому началу термодинамики. Это проявляется в том, что первое начало не привело ни к какой рациональной шкале температур.
Второе начало термодинамики, наоборот, позволяет судить о направлении процессов, которые могут происходить в действительности. Но этим значение второго начала не исчерпывается.
Второе начало позволяет вполне удовлетворительно решить вопрос о количественной мере температуры и построить рациональную температурную шкалу, не зависящую от произвола выбора термодинамического тела и устройства термометра.
Оно, совместно с первым началом, позволяет также установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состоянии термодинамического равновесия. Все такие точные соотношения получили общее называние термодинамических соотношений.
Основоположником второго начала термодинамики считается французский инженер и физик Сади Карно. В своем сочинении «О движущей силе огня и о машинах, способных развивать эту силу», вышедшем в 1824 г. (т.е. значительно ранее открытия первого начала Майером, Джоулем и Гельмгольцем), Карно исследовал условия
превращения теплоты в работу.
Однако тогда Карно стоял на точке зрения теории теплорода (позднее он от нее отказался), а поэтому ему не удалось дать ясную и четкую формулировку второго начала термодинамики. Это было сделано только в 1850-1851 гг. независимо друг от друга немецким физиком Рудольфом Клаузиусом и шотландским физиком Вильямом Томсоном (лордом Кельвином).
Они сформулировали основной постулат, выражающий второе начало термодинамики, и вывели из него главнейшие следствия.
Различные формулировки основного постулата, выражающего второе начало термодинамики
Чтобы перейти к формулировке постулата второго начала термодинамики, следуя историческому ходу идей, рассмотрим схематически работу тепловой машины.
В цилиндре машины (рис. 23) помещается газ или какое-либо другое вещество, называемое рабочим телом. Для определенности будем считать, что рабочим телом является газ. Пусть на диаграмме 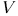начальное состояние рабочего тела изображается точкой 1.
Приведем дно цилиндра в тепловой контакте нагревателем, т.е. телом, температура которого выше температуры газа в цилиндре. Газ будет нагреваться и расширяться — этот процесс изображен кривой 
. Рабочее вещество получит от нагревателя теплоту 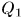и совершит положительную работу 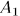. По первому началу
Теперь надо вернуть поршень в исходное положение, т.е. сжать газ. Это надо сделать так, чтобы работа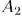 
, затраченная на сжатие, была меньше 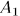. С этой целью приведем дно цилиндра в тепловой контакт с холодильником., т.е. телом, температура которого ниже температуры газа в цилиндре, и сожмем газ по пути 
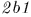. В результате газ вернется в исходное состояние 1. При этом он отдаст холодильнику количество теплоты 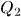. По первому началу
Отсюда в комбинации с (28.1)
Таким образом, тепловая машина совершила круговой процесс, в результате которого нагреватель отдал количество теплоты 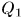, холодильник получил количество теплоты 
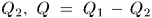пошло на производство работы 
Отношение
называется коэффициентом, или экономическим коэффициентом полезного действия (КПД) тепловой машины.
Обратимые и необратимые процессы
Если в результате какого-либо процесса система переходит из состояния 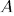в другое состояние 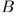и если возможно вернуть ее хотя бы одним способом в исходное состояние 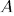и притом так, чтобы во всех остальных телах не произошло никаких изменений, то этот процесс называется обратимым. Если же это сделать невозможно, то процесс называется необратимым.
Примером необратимого процесса может служить переход теплоты от более нагретого тела к телу менее нагретому при тепловом контакте этих тел. Необратимость такого процесса непосредственно следует из постулата Клаузиуса. Необратимым является процесс получения теплоты путем трения. Его необратимость является непосредственным следствием постулата Томсона-Планка.
Если систему из конечного состояния 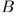можно вернуть в исходное состояние 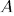безразлично каким способом, не требуя, чтобы она обязательно проходила через ту же последовательность состояний, что и в прямом процессе 
, то такой процесс называют обратимым в широком смысле слова.
Если же возможен обратный процесс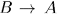 
, переводящий систему в исходное состояние 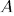через ту же последовательность состояний, через которую прошла система в прямом процессе , то процесс называется обратимым в узком смысле слова. Всякий процесс, обратимый в узком смысле, очевидно, обратим и в широком смысле слова.
Ясно, что процесс, обратимый в узком смысле, необходимо должен быть квазистатическим. Действительно, неквазистатический процесс идет с какой-то скоростью, отличной от нуля.
Если же скорость отлична от нуля, то она должна входить в число внутренних параметров, определяющих состояние системы. Но тогда состояния системы в прямом и обратном процессах не могут быть тождественными — они всегда будут отличаться направлениями своих скоростей.
Это различие исчезнет только в пределе, когда процесс идет квазистатически — бесконечно медленно.
Обратно, если внутренние параметры системы в состоянии равновесия определяются внешними условиями однозначно, то всякий квазистатический процесс будет обратимым в узком смысле. Оговорка об однозначности существенна, так как в приводимом ниже доказательстве используется следующее положение.
Если внешними воздействиями система выводится из положения равновесия, то по устранении этого воздействия она в конце концов возвращается в прежнее равновесное состояние. Если же однозначности нет, то может произойти переход и в другие равновесные состояние.
Приведем теперь само доказательство, хотя после сделанных разъяснений почти самоочевидно. Квазистатический процесс есть бесконечно медленный процесс, состоящий из последовательности состояний равновесия, точнее, состояний, бесконечно мало отличающихся от равновесных. Если взять какое-либо равновесное состояние, то но самому определению равновесия в отсутствие внешних воздействий оно будет сохраняться неограниченно долго.
Чтобы начался процесс, надо с помощью внешних воздействий нарушить равновесие, т.е. менять внешние параметры и температуру окружающей среды. Для квазистатичности процесса необходимо, чтобы эти изменения совершались настолько медленно, чтобы в каждый момент времени система находилась либо в равновесном состоянии, либо в состоянии, как угодно мало отличающемся от равновесного.
В пределе получится идеализированный процесс, идущий с бесконечно малой скоростью и состоящий из последовательных состояний равновесия. С помощью таких процессов можно перевести систему из начального состояния 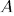в конечное состояние 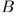, отстоящее от начального как угодно далеко: для этого требуется только достаточно большое время. Конкретно, существенные изменения состояния системы должны совершаться за времена очень большие по сравнению с временами релаксации.
Если изменить знаки бесконечно малых приращений внешних параметров и температуры на противоположные, то система снова вернется в исходное состояние 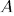, проходя в обратном порядке через состояния, бесконечно мало отличающиеся от состояний, через которые она проходила ранее. В пределе, когда прямой и обратный процессы сделаются строго равновесными, исчезнет и это бесконечно малое различие.
При этом в результате прямого и обратного процесса в окружающих телах не произойдет никаких изменений, поскольку внешние параметры и температура окружающей среды вернутся в точности к своим исходным значениям. Таким образом, при оговоренной выше однозначности квазистатический процесс не только обратим вообще, но обратим в узком смысле слова.
Это утверждение постоянно используется в термодинамике. В частности, при том же условии всякий квазистатический круговой процесс может происходить как в прямом, так и в обратном направлении. Ниже, когда квазистатичность и обратимость являются синонимами, употребляется термин «квазистатический».
В качестве примера, иллюстрирующего приведенные рассуждения, рассмотрим адиабатически изолированную систему — газ в цилиндре с поршнем, который может в нем свободно перемещаться. Внешнее давление 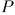можно осуществить, положив на поршень груз.
Для того чтобы груз можно было увеличивать или уменьшать малыми порциями, предположим, что поршень нагружен мелким песком. Пусть газ адиабатически расширяется, переходя из начального равновесного состояния 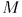в конечное равновесное состояние (рис. 24).
Этот процесс можно осуществить, снимая с поршня песчинку за песчинкой. Снимем сначала одну песчинку. Внешнее давление уменьшится, а газ расширится. Это расширение очень мало, и его трудно заметить.
Но по существу оно представляет собой неравновесный процесс, сопровождающийся весьма сложными макроскопическими движениями газа. Однако в конце концов газ придет в состояние равновесия, и это состояние изобразится на графике точкой 1. Сняв вторую песчинку, заставим газ совершить второй неравновесный процесс, переводящий его в равновесное состояние 2.
Повторив эту операцию 
раз, переведем газ в конце концов в равновесное состояние , пройдя при этом через конечное состояние 
равновесных состояний 
. Каждое из этих состояний получается из предыдущего путем малого, но неравновесного процесса, так что процесс 
в целом является неравновесным.
Попытаемся теперь вернуть газ в исходное состояние , последовательно нагружая поршень по одной песчинке. При этом мы пройдем через ту же конечную последовательность равновесных состояний 
что и в прямом процессе.
Однако промежуточные малые неравновесные процессы будут уже иными. Например, в обратном процессе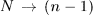 
газ сжимается при несколько большем давлении (число песчинок на поршне больше на одну), чем в прямом процессе 
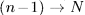. Поэтому при обратном процессе над газом надо совершить несколько большую работу, чем в прямом процессе. Процесс 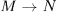, состоящий из конечного числа равновесных состояний, в целом является необратимым.
Допустим теперь, что вес песчинки неограниченно уменьшается, а общее число песчинок неограниченно растет, однако так, что общий вес песка остается неизменным. Тогда в пределе неравновесный процесс
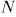. Той же линией, но проходимой в противоположном направлении, изобразится и обратный процесс. Работа, совершаемая газом как в прямом, так и в обратном процессе, численно одна и та же и изображается площадью криволинейной трапеции, ограниченной сверху кривой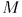 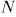. Для приведения газа в исходное состояние должна быть затрачена такая же работа, какую совершил сам газ при расширении. Ясно поэтому, что квазистатическое расширение газа, которое мы рассмотрели, есть процесс обратимый и притом в узком смысле слова.
Задача 1. Моль идеального газа с постоянной теплоемкостью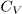 
заключен в цилиндр с адиабатическими стенками и поршнем, который может перемещаться в цилиндре без трения. Поршень находится под постоянным внешним давлением 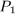. В некоторый момент времени внешнее давление скачкообразно уменьшают или увеличивают до 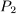. (Этого можно достигнуть. снимая часть груза с поршня или добавляя новый груз.) В результате газ адиабатически изменяет свой объем. Вычислить температуру и объем газа после того как установится термодинамическое равновесие.
Решение. Теплота, полученная газом при адиабатическом расширении или сжатии, равна нулю. Работа, совершаемая газом,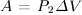 
, поэтому 
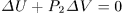. Так как 
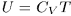, то отсюда находим
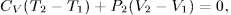или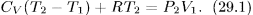 
Следовательно,
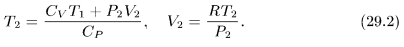
Цикл Карно и теорема Карно
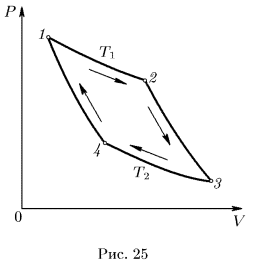
Из различных круговых процессов особое значение в термодинамике имеет круговой процесс, или процесс Карно. Это квазистатический процесс, в котором систему можно приводить в тепловой контакт с двумя тепловыми резервуарами, имеющими постоянные температуры 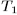и 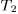. В дальнейшем предполагается, что 
.
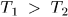Тепловой резервуар с более высокой температурой 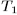называется нагревателем, а с более низкой температурой 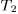— холодильником. Цикл Карно заключается в следующем. Сначала система, имея температуру 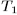, приводится в тепловой контакт с нагревателем. Затем, бесконечно медленно уменьшая внешнее давление, ее заставляют квазистатически расширяться по изотерме 12 (рис. 25).
При этом она заимствует теплоту 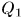от нагревателя и производит работу 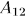против внешнего давления. После этого систему адиабатически изолируют и заставляют квазистатически расширяться по адиабате 23, пока ее температура не достигнет температуры холодильника 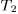. При адиабатическом расширении
система также совершает некоторую работу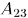 
против внешнего давления.
В состоянии 3 систему приводят в тепловой контакт с холодильником и непрерывным увеличением давления изотермически сжимают ее до некоторого состояния 4. При этом над системой производится работа (т.е. сама система совершает отрицательную работу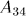 
), и она отдает холодильнику некоторое количество теплоты .
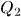Состояние выбирается так. чтобы можно было квазистатическим сжатием по адиабате 14 вернуть систему в исходное состояние 1. Для этого надо, разумеется, над системой совершить работу (т.е. сама система должна произвести отрицательную работу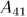 
). В результате кругового процесса Карно внутренняя энергия системы не изменится, а поэтому произведенная ею работа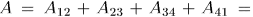 
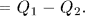Коэффициент полезного действия 
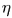цикла Карно определяется соотношением (28.4), из которого следует
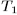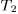Докажем знаменитую теорему Карно: коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур и нагревателя и холодильника, но не зависит от устройства машины, а также от вида используемого рабочего вещества.
Для доказательства рассмотрим две машины Карно, имеющие общий нагреватель при температуре 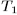и общий холодильник при температуре 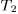. Пусть КПД первой машины равен 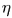, а второй 
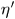. Допустим, что 
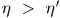, и покажем, что это допущение приводит к противоречию с постулатом второго начала термодинамики.
Цикл Карно — квазистатический, а потому он может совершаться как в прямом, так и в обратном направлении, т.е. производить работу. Пусть в результате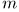 
циклов она отберет от нагревателя теплоту 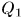, передаст холодильнику теплоту 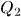и произведет работу 
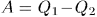, например, поднимет груз.
Остановим после этого первую машину и используем потенциальную энергию поднятого груза, чтобы привести в действие вторую машину в обратном направлении.
Вторая машина Карно будет, следовательно, работать как холодильная машина. Пусть в результате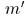 
циклов она заберет теплоту 
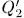от холодильника и передаст теплоту 
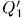нагревателю; при этом над машиной будет совершена работа 
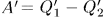. Результат действия 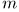циклов первой и 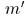циклов второй машины представится схемой
нагреватель отдал теплоту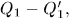 
холодильник отдал теплоту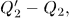 
машина совершила работу
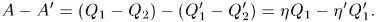
Дальнейший ход доказательства зависит от того, какой постулат второго начала термодинамики положить в основу: постулат Томсона-Планка или постулат Клаузиуса. Если исходить из постулата Томсона-Планка, то доказательство следует вести так. Выберем целые числа 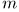и 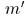так, чтобы 
.
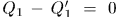Это всегда можно достигнуть. Действительно,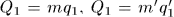 
, где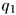 
— количество теплоты, полученное первой машиной от нагревателя в результате одного цикла, a 
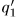— количество теплоты, отданное тому же нагревателю второй машиной также в результате одного цикла. Есл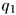и и 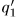соизмеримы, то всегда можно подобрать целые числа 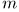и 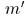так, чтобы 
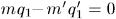, т.е. .
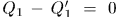Если же эти величины не соизмеримы, то целые числа 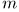и 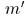можно выбрать настолько большими, чтобы это равенство выполнялось с какой угодно заранее заданной точностью. Поэтому физически всегда возможно выбрать целые числа 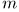и 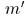так, чтобы 
.
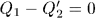Тогда результат кругового процесса представится в виде:
- состояние нагревателя не изменилось,
- холодильник отдал теплоту
- машина совершила работу
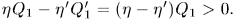
Таким образом, единственным результатом кругового процесса будет производство работы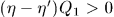 
за счет эквивалентного количества теплоты, заимствованной от холодильника.
Это процесс Томсона-Планка, возможность которого противоречит постулату второго начала термодинамики. Поэтому предположение 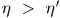неверно так же неверно предположение 
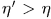. Чтобы убедиться в этом, надо заставить вторую машину пройти цикл Карно в прямом, а первую — в обратном направлении и повторить наше рассуждение. Следовательно, 
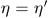, и теорема Карно доказана.
Если в основу доказательства положить постулат Клаузиуса, то рассуждение немного изменится. Выберем целые числа 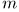и 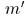так, чтобы работа, выполненная обеими машинами, равнялась нулю: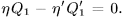 
Тогда результат кругового процесса представится в виде:
- нагреватель получил теплоту
- холодильник отдал теплоту
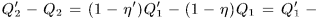
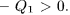
Никаких других изменений не произошло. Единственным результатом процесса получился переход теплоты от тела менее нагретого к телу более нагретому. Это противоречит постулату Клаузиуса, что и доказывает теорему Карно.
