| 🎓 Заказ №: 21983 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
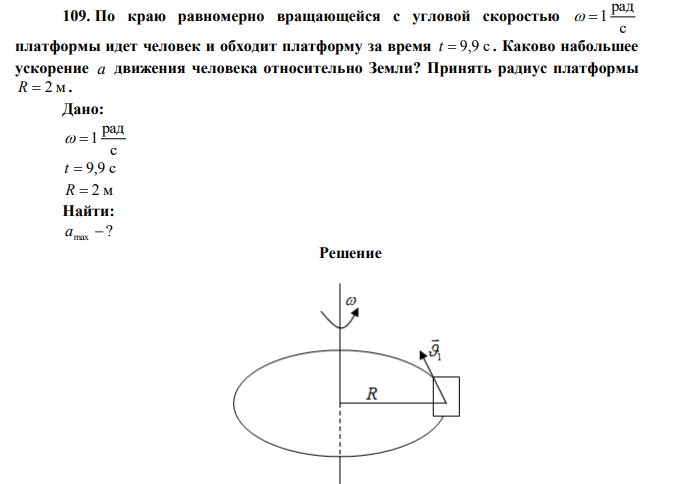
По краю равномерно вращающейся с угловой скоростью с рад 1 платформы идет человек и обходит платформу за время t 9,9 с . Каково набольшее ускорение а движения человека относительно Земли? Принять радиус платформы R 2 м .
Решение Если человек идет по краю круглой платформы, он имеет центростремительное ускорение a , которое равно: R a 2 (1) Где – скорость человека относительно Земли; R – радиус платформы. Если человек за время t обходит платформу, то его относительно платформы, равна: t R t l 2 1 (2) Скорость человека относительно Земли будет максимальна тогда, когда он будет идти в направлению вращения платформы. При этом можем записать: 1 2 Где 2 – скорость вращения платформы. Выразим эту скорость платформы через ее угловую скорость : 2 R Из последних трех соотношений можем записать: t R R t 2 R 2 (3)

| Научись сам решать задачи изучив физику на этой странице: |
| Услуги: |
Готовые задачи по физике которые сегодня купили:
- Скорость самолета с реактивным двигателем ч км 950 .
- Двухпроводная линия состоит из длинных параллельных прямых проводов, находящихся на расстоянии d 4 мм друг от друга. По проводам текут одинаковые токи I 50 А .
- Два одинаковых по модулю разноименных заряда находятся на расстоянии 1 м.
- В цепь переменного тока напряжением 220 В включены последовательно емкость, активное сопротивление 10 Ом и индуктивность.
- Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра излучением с длиной волны 80 нм.
- Найти длину волны де Бройля для электрона, имеющего кинетическую энергию T 1 МэВ .
- Найти емкость C сферического конденсатора с радиусами обкладок R1 2,0 см и R2 2,6 см , между сферическими обкладками которого находятся два концентрических слоя диэлектрика, толщины и диэлектрические проницаемости которых равны соответственно d1 0,2 см , d2 0,4 см , 1 7 , 2 2 .
- Человек массой 60 кг стоит на краю платформы, имеющей форму диска массой 100 кг и радиусом 6 м, вращающейся с угловой скоростью 0,25 рад/с.
- В однородном магнитном поле с индукцией B 0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l 15 см .
- За какое время Солнце уменьшит сою массу на 1000 кг за счет излучения? Максимум испускательной способности Солнца приходится на длину волні 500 нм.
