Для связи в whatsapp +905441085890

При изобарном нагревании газа на T1  100 К требуется Q12  4,2 кДж теплоты, а при изохорном охлаждении газ отдает Q23  5,04 кДж теплоты при уменьшении давления в два раза.

🎓 Заказ №: 21974
⟾ Тип работы: Задача
📕 Предмет: Физика
✅ Статус: Выполнен (Проверен преподавателем)
🔥 Цена: 198 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

При изобарном нагревании газа на T1  100 К требуется Q12  4,2 кДж теплоты, а при изохорном охлаждении газ отдает Q23  5,04 кДж теплоты при уменьшении давления в два раза. Начальная температура газа при изохорном охлаждении T2  400 К . Постройте графики этих процессов в координатах p V . Определите коэффициент Пуассона для этого газа. Найдите изменение энтропии S для каждого из изопроцессов и для всего процесса в целом.

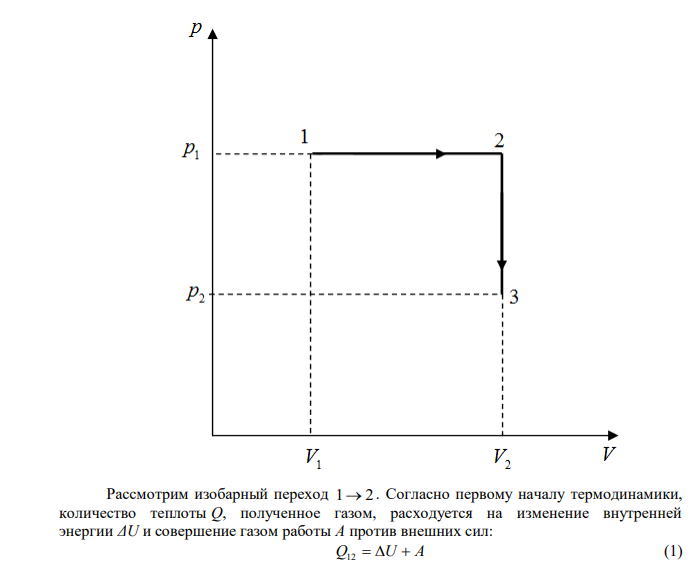
Решение Согласно условию задачи, сначала происходило изобарное нагревание газа (нагревание при постоянном давлении), а потом изохорное уменьшение давление газа в два раза. Построим графики этих процессов в координатах p V : Рассмотрим изобарный переход 1 2 . Согласно первому началу термодинамики, количество теплоты Q, полученное газом, расходуется на изменение внутренней энергии ΔU и совершение газом работы А против внешних сил: Q12  U  A (1) Изменение внутренней энергии определяется формулой: 1 2 R T i U    (2) Где i – число степеней свободы (для кислорода i=5);  – количество молей газа; К Дж R  8,31 – универсальная газовая постоянная; T1 – изменение температуры. Работа газа при изобарном процессе равна:   A  p1 V2 V1 (3) Где 1 p – давление газа; V1 – начальный объем газа; V2 – конечный объем газа. Запишем уравнение Менделеева – Клапейрона для двух состояний газа: pV1 RT1 pV2 RT2 Где p – давление газа; К Дж R  8,31 – универсальная газовая постоянная; V – объем газа; T – температура газа. Из последних двух выражений можем записать:     p V2 V1 R T2 T1 (4) Из уравнений (3) и (4) видим, что работу можно выразить формулой:   A R T2 T1 (5)

При изобарном нагревании газа на T1  100 К требуется Q12  4,2 кДж теплоты, а при изохорном охлаждении газ отдает Q23  5,04 кДж теплоты при уменьшении давления в два раза. Начальная температура газа при изохорном охлаждении T2  400 К . Постройте графики этих процессов в координатах p V . Определите коэффициент Пуассона для этого газа. Найдите изменение энтропии S для каждого из изопроцессов и для всего процесса в целом.
При изобарном нагревании газа на T1  100 К требуется Q12  4,2 кДж теплоты, а при изохорном охлаждении газ отдает Q23  5,04 кДж теплоты при уменьшении давления в два раза. Начальная температура газа при изохорном охлаждении T2  400 К . Постройте графики этих процессов в координатах p V . Определите коэффициент Пуассона для этого газа. Найдите изменение энтропии S для каждого из изопроцессов и для всего процесса в целом.
При изобарном нагревании газа на T1  100 К требуется Q12  4,2 кДж теплоты, а при изохорном охлаждении газ отдает Q23  5,04 кДж теплоты при уменьшении давления в два раза. Начальная температура газа при изохорном охлаждении T2  400 К . Постройте графики этих процессов в координатах p V . Определите коэффициент Пуассона для этого газа. Найдите изменение энтропии S для каждого из изопроцессов и для всего процесса в целом.

Научись сам решать задачи изучив физику на этой странице:
Услуги:

Готовые задачи по физике которые сегодня купили:

  1. Два самолета, летящие на одной высоте с одинаковой скоростью, одновременно вылетают из точки, расположенной на экваторе, и облетают Землю по экватору в противоположных направлениях – с востока на запад и с запада на восток.
  2. Заряженная частица прошла ускоряющую разность потенциалов 10 В 4 U  и влетела в скрещенные под прямым углом электрическое и магнитное поля.
  3. Фотон с импульсом с м p   кг 22 1 5,44 10 рассеялся на свободном покоившемся электроне, в результате чего его импульс стал равен с м p   кг 22 2 1,36 10 .
  4. Точка движется в плоскости xoy по закону: 2 t x  , y = t1 t .
  5. Как изменится изображение предмета линзой, если половину линзы закрыть непрозрачным экраном?
  6. Определить токи, текущие через сопротивления R1 , R2 , R3 , если  1  12,5 В ,  2 10 В , R1 1Ом , R2  5 Ом , R3  7,5 Ом.
  7. Брусок массой m = 2,0 кг медленно подняли по шероховатой наклонной поверхности на высоту h = 51 см при помощи нити, параллельной этой плоскости.
  8. Шар массой m 2 кг 1  движется со скоростью с м 1  3 и сталкивается с шаром массой m 1 кг 2  , движущемся ему навстречу со скоростью с м 2  4 .
  9. На рисунке показано сечение трех прямых длинных проводников с током.
  10. К сети переменного тока (120 В; 50 Гц) присоединены параллельно конденсатор (20 мкФ) и катушка (100 Ом; 0,5 Гн).