Решение уравнения Шредингера для микрочастицы массой m в бесконечно глубокой одномерной потенциальной яме шириной l можно записать в виде: ikx ikx C e C e    1  2 , где  mE K 2 .

🎓 Заказ №: 21915

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

Решение уравнения Шредингера для микрочастицы массой m в бесконечно глубокой одномерной потенциальной яме шириной l можно записать в виде: ikx ikx C e C e    1  2 , где  mE K 2  . Используя граничные условия нормировки  — функции, определить: 1) коэффициенты C1 и С2; 2) собственные значения энергии En. Найти выражение для собственной нормированной  -функции.

Решение Согласно условию задачи нам дана функция: ikx ikx C e C e    1  2 (1) Перепишем функцию (1) в другом виде, используя формулу Эйлера: C cos kx isin kx C cos kx isin kx   1   2  (2) Поэтому можем записать:       1 2 0 1 2  0  C cos0  isin 0 C cos0  isin  C  C (3) На стенках функция Ψ(x) должна обращаться в нуль, т.е. должно выполняться граничное условие Ψ(0) = Ψ(l) = 0. Используем граничное условие, согласно которому Ψ(0)=0. Учитывая это, из выражения (3) имеем: C1  C2  0 C1  C2 (4) Используя условие нормировки, согласно которому можем записать:    l dx 0 2 1 (5) Подставим (2) в (5):                     2 1 2 4 2 1 4 2 1 cos 2 sin sin 4 sin 4 cos sin cos sin cos sin cos sin cos sin cos sin cos sin cos sin 2 2 2 2 0 2 2 0 2 2 0 2 2 2 0 2 2 2 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 1 2                                        C l l dx C x C k x C i k x C i k x dx C k xdx C C k x C i k x C k x C i k x dx C k x C i k x C k x i k x dx C k x i k x C k x i k x dx C k x i k x C k x i k x dx l l l l l l l l l C 2 1 2  (6)

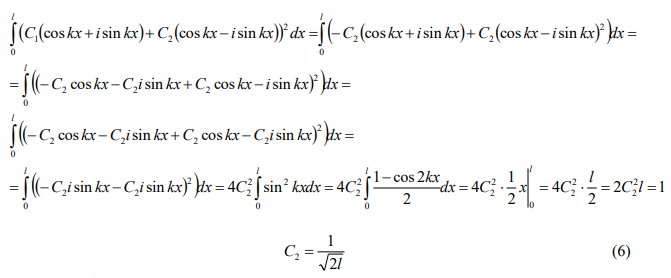
Научись сам решать задачи изучив физику на этой странице: Решение задач по физике

Услуги: Заказать физику Помощь по физике

Готовые задачи по физике которые сегодня купили:

1. На противоположных концах стоящей на рельсах железнодорожной платформы закреплены две пушки.
2. Мыльная пленка с показателем преломления n  1,33 , расположенная вертикально, образует клин вследствие стекания жидкости.
3. Два заряда Q 10 нКл 1   и Q 20 нКл 2  находятся на расстоянии l  20 см друг от друга.
4. Чему равна степень поляризации P света, представляющего собой смесь естественного света с поляризованным, если отношение интенсивности поляризованного света к интенсивности естественного равно 5?
5. В сосуде объемом 30 л находится некоторый газ, который имеет температуру, соответствующую средней скорости движения молекул 493 м/с.
6. Электрон влетел в однородное магнитное поле, индукция которого 200 мТл, перпендикулярно силовым линиям поля и описал дугу радиусом 5 см.
7. Определите, при какой температуре идеального газа число молекул в заданном интервале  ,   d будет максимально?
8. Определить плотность воздуха при температуре t = 307°С и давлении р = 98,1 кПа.
9. Заряд Q=1 нКл перемещается под действием сил поля из одной точки поля в другую, при этом совершается работа А=0,2 мкДж.
10. За t=4 минуты колебаний математического маятника длиной 0,5 м, амплитуда уменьшилась в 1,5 раза.