Для связи в whatsapp +905441085890

Определить емкость C слоистого цилиндрического конденсатора, высота которого h 10,0 см , радиус внутренней обкладки R1  2,0 см , радиус внешней обкладки R2  2,6 см , между обкладками которого находятся два цилиндрических слоя диэлектрика, толщины и диэлектрическая проницаемость которых равны соответственно d1  0,4 см , d2  0,2 см, 6  1  ,  2  7

🎓 Заказ №: 21968
⟾ Тип работы: Задача
📕 Предмет: Физика
✅ Статус: Выполнен (Проверен преподавателем)
🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

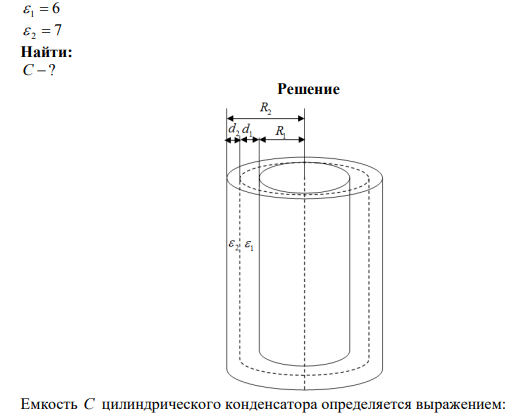
Определить емкость C слоистого цилиндрического конденсатора, высота которого h 10,0 см , радиус внутренней обкладки R1  2,0 см , радиус внешней обкладки R2  2,6 см , между обкладками которого находятся два цилиндрических слоя диэлектрика, толщины и диэлектрическая проницаемость которых равны соответственно d1  0,4 см , d2  0,2 см, 6  1  ,  2  7

Решение Емкость C цилиндрического конденсатора определяется выражением: C  (1) где 12 0 8,85 10    Ф/м – электрическая постоянная;  – диэлектрическая проницаемость среды между обкладками конденсатора; h – высота цилиндрического конденсатора; R1 – радиус внутренней обкладки цилиндрического конденсатора; R2 – радиус внешней обкладки цилиндрического конденсатора. В нашем случае между обкладками цилиндрического конденсатора находятся два цилиндрических слоя диэлектрика, толщины, которых 1 d и 2 d , соответственно. Тогда данная система представляет собой два цилиндрических конденсатора, соединенных последовательно. При этом: радиус внутренней обкладки первого цилиндрического конденсатора равен 1 / R1  R , а радиус внешней обкладки первого цилиндрического конденсатора равен 1 1 / R2  R  d . Соответственно, радиус внутренней обкладки второго цилиндрического конденсатора равен 1 1 // R1  R  d , а радиус внешней обкладки второго цилиндрического конденсатора равен 2 // R2  R .

Определить емкость C слоистого цилиндрического конденсатора, высота которого h 10,0 см , радиус внутренней обкладки R1  2,0 см , радиус внешней обкладки R2  2,6 см , между обкладками которого находятся два цилиндрических слоя диэлектрика, толщины и диэлектрическая проницаемость которых равны соответственно d1  0,4 см , d2  0,2 см, 6  1  ,  2  7
Определить емкость C слоистого цилиндрического конденсатора, высота которого h 10,0 см , радиус внутренней обкладки R1  2,0 см , радиус внешней обкладки R2  2,6 см , между обкладками которого находятся два цилиндрических слоя диэлектрика, толщины и диэлектрическая проницаемость которых равны соответственно d1  0,4 см , d2  0,2 см, 6  1  ,  2  7
Определить емкость C слоистого цилиндрического конденсатора, высота которого h 10,0 см , радиус внутренней обкладки R1  2,0 см , радиус внешней обкладки R2  2,6 см , между обкладками которого находятся два цилиндрических слоя диэлектрика, толщины и диэлектрическая проницаемость которых равны соответственно d1  0,4 см , d2  0,2 см, 6  1  ,  2  7

Научись сам решать задачи изучив физику на этой странице:
Услуги:

Готовые задачи по физике которые сегодня купили:

  1. На нагревание 40 г кислорода от 16 до 40 0С затрачено 628,5 Дж.
  2. Пучок естественного света падает на систему из N  6 николей, плоскость пропускания каждого из которых повернута на угол 0 30 относительно плоскости пропускания предыдущего николя.
  3. При каком значении угла падения светового луча на границу раздела двух сред (с показателями преломления 1 n и 2 n ) отраженный и преломленный лучи образуют угол?
  4. Поток магнитной индукции через площадь поперечного сечения соленоида (без сердечника) равен Ф  2 мкВб . Длина соленоида l  12,5 см .
  5. Оптическая разность хода от двух когерентных источников в некоторой точке пространства   8,723 мкм.
  6. При адиабатическом расширении углекислого газа с количеством   2 моль его температура понизилась на t C 0   20 .
  7. Точка начинает двигаться по плоскости xoy из начала координат с ускорением a i tj     2  3 .
  8. Найти наибольший порядок спектра для желтой лини натрия с длиной волны м 7 5,89 10    , если период дифракционной решетки d  2 мкм .
  9. Полагая, что звезда обладает свойствами абсолютно черного тела и максимум испускательной способности приходится на длину волны 0,48 мкм, определить температуру Т поверхности звезды.
  10. По уравнению Ван-дер-Ваальса определить температуру Т азота, находящегося под давлением р = 10 МПа, если плотность его ρ = 140 кг/м3.