Шаровой слой, равномерно заряженный по объему с постоянной объемной плотностью 3 1 м нКл   , имеет внутренний радиус R1  3 см и внешний R2  5 см .

🎓 Заказ №: 21974

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 198 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

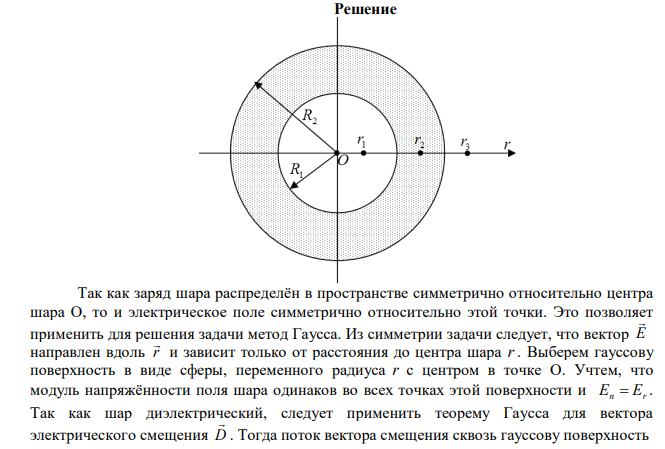
Шаровой слой, равномерно заряженный по объему с постоянной объемной плотностью 3 1 м нКл   , имеет внутренний радиус R1  3 см и внешний R2  5 см . Определить напряженность Е электрического поля в точках, отстоящих от шарового слоя на расстояниях r1  2 см , r2  4 см и r3  6 см . Построить график зависимости напряженности Е от r .

Решение Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор E  направлен вдоль r  и зависит только от расстояния до центра шара r . Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и En  Er . Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения D  . Тогда поток вектора смещения сквозь гауссову поверхность 2 DdS D dS D dS DS D 4 r S S n S            (1) Где S – площадь гауссовой поверхности, r – её радиус. Всё пространство можно разбить на 3 области: 1-ая: 0 1 R1  r  2-ая: 1 2 R2 R  r  3-ья: 3 R2 r  Применим теорему Гаусса для каждой области. Для области 0 1 R1  r  . Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смещения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю: D1  0 , 0 0 1    D E где 12 0 8,85 10    Ф/м – электрическая постоянная Для области 1 2 R2 R  r  Свободный заряд, охватываемый гауссовой поверхностью, может быть выражен через объём той части шара, которая попала внутрь сферы радиусом 2 r :     3 1 3 2 3 4 qсвоб  V  r  R (2)

Научись сам решать задачи изучив физику на этой странице: Решение задач по физике

Услуги: Заказать физику Помощь по физике

Готовые задачи по физике которые сегодня купили:

1. Идеальный двухатомный газ количеством вещества 1 моль совершает политропический процесс.
2. Напишите уравнение гармонического колебательного движения, если максимальное ускорение точки 2 49,3 с см , период колебаний 2 с, смещение  точки от положения равновесия в начальный момент времени равно 25 мм.
3. Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов.
4. Маховик радиусом R  10 см может без трения вращаться вокруг горизонтальной оси.
5. Частица 1 массой m1, летящая со скоростью  , столкнувшись с неподвижной частицей 2 массой М, отскакивает от нее и летит в противоположном направлении со скоростью 2 1  u .
6. Зависимость пройденного телом пути от времени задается уравнением 2 3 S  A Bt Ct  Dt , где А= 6 м, В=3м/с, С= 2 м/с2 , D=1м/с3 .
7. Вычислите удельные теплоемкости при постоянном объеме сv и при постоянном давлении ср для водорода и неона, принимая эти газы за идеальные.
8. Найдите импульс, полную и кинетическую энергии электрона, движущегося со скоростью   0,9c , где с м c 8  310.
9. Совершая цикл Карно, идеальный газ получил от нагревателя 1 кДж теплоты.
10. Определите плотность  водяных паров в критическом состоянии.